Тема 2.3 Экономико-математические методы и модели в организации перевозочного процесса в НГХК

Схемы организации перевозочного процесса.

С точки зрения организации перевозочного процесса возможны три основные схемы.

«Один-к-одному». Первая схема организации перевозок, наиболее простая с точки зрения планирования, «один-к-одному», когда перевозка груза осуществляется в течение дня (рейса) между одним отправителем и получателем, не требует от автотранспортного предприятия решения ни транспортной задачи, ни задачи маршрутизации.

«Один-ко-многим». Один отправитель – несколько получателей. Перевозки по второй схеме («один-ко-многим») требует решения задачи маршрутизации, которая включает в себя решение: о задачи «увязки» ездок, если между грузоотправителями и грузополучателями перевозка осуществляется только по маятниковым маршрутам; о задачи коммивояжера, если между грузоотправителями и грузополучателями перевозка осуществляется только по развозочным (сборным или сборно-развозоч-ным) маршрутам; о двух вышеперечисленных типов задач, если при организации перевозочного процесса используются как маятниковые, так и развозочные (сборные или сборно-развозочные) маршруты.

Перевозка груза осуществляется по развозочному маршруту, если в качестве первого объекта выступает грузоотправитель и второго — грузополучатель, в противном случае организуется сборный маршрут. В случае, когда первый и второй объекты являются как грузообразующи-ми, так и грузопоглощающими пунктами, для перевозки груза используется сборно-развозочный маршрут.

«Многие-ко-многим». Несколько отправителей – несколько получателей. При организации движения по схеме «многие-ко-многим» требуется на первом этапе решить транспортную задачу, затем задачу маршрутизации (второй этап).

Проектирование технологии организации перевозочного процесса.

Логистический подход к организации автомобильных перевозок обусловливает новое методологическое содержание, заключающееся в том, что основной составляющей частью перевозок должно стать проектирование оптимального (рационального) перевозочного процесса. Под этим понимается поиск наилучших организационных и технически возможных решений, обеспечивающих максимальную эффективность перевозки грузов от места их производства до места потребления. Следует отметить, что понятие «проектирование» означающее дословно выбор задуманного предначертания, представляется правомерным относить к процессу создания не только технических средств, но и транспортной продукции.

На рис. 3 показана принципиальная схема организации перевозки груза.

Здесь обозначено: I – грузообразующий пункт; II – грузопоглащающий пункт; III – перевозочный комплекс; W(t) – грузопоток перевозочного комплекса; WQ – транспортная продукция; Wг – потребности грузополучателя; W’k – плановая провозная возможность перевозочного комплекса; Wk - фактическая провозная возможность перевозочного комплекса; О1,О2,О3 - операторы.

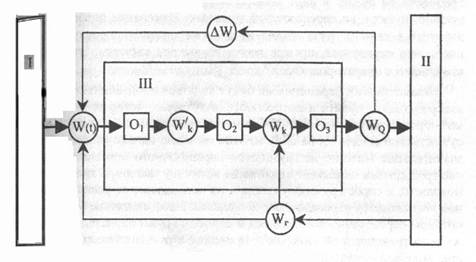
Рис. 3 Принципиальная схема организации перевозки груза.

Под грузообразующими пунктами понимаются предприятия и организации всех отраслей народного хозяйства, с которых вывозятся их продукция и отходы.

Под грузопоглощающими пунктами понимаются предприятия и организации всех отраслей народного хозяйства, на которые завозятся сырье, топливо, материалы, готовая продукция и другие грузы, необходимые для их нормальной производственной деятельности.

Расположение грузообразующих и грузопоглощающих пунктов определяется, с одной стороны, природными условиями, а с другой – более или менее случайными факторами.

Одно и тоже предприятие может одновременно быть грузообразующим и грузопоглощающим пунктом. Например, завод железобетонных изделий, как вывозящий готовую продукцию является грузообразующим пунктом, а как ввозящий сырье – песок, щебень, цемент, и т.д. – грузопоглощающим.

В данной принципиальной схеме можно выделить два контура. 1 – количество груза, доставленного грузополучателю WQ, должно соответствовать грузопотоку перевозочного комплекса W(t). Разница между входом и выходом ΔW=W(t)-WQ подается по цепи обратной связи на грузообразующий пункт и через оператора О1 изменяет плановую величину провозной возможности перевозочного комплекса. Оператор О1 приводит в соответствие связь между грузопотоком и провозной возможностью перевозочного комплекса. Планируемая величина его провозной возможности W’k в свою очередь преобразуется в действительную провозную возможность Wk с помощью оператора О2.

Второй контур представляет собой изменение в объеме перевозок, связанные со спросом получателя на данную продукцию (груз). Свои потребности он подает в виде заказов по другой цепи связи на грузообразующий пункт и на перевозочный комплекс. Изменение потребности получателя в данном грузе влияет на действительную провозную возможность, что отражается, прежде всего, на выходе системы. Это действие выполняется оператором О3.

Независимыми переменными будут являться производительность грузообразующего пункта и потребность получателя, которые могут принимать произвольные значения.

Классическая транспортная задача.

Транспортная задача (классическая) — задача об оптимальном плане перевозок товара со складов в пункты потребления на транспортных средствах.
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку).

Классическая транспортная задача является одной из важнейших задач линейного программирования, и заключается она в нахождении оптимальных грузопотоков, то есть в оптимальном закреплении поставщиков однородного груза за потребителями (несколько складов и большое количество потребителей).
Исходные данные
Исходными данными для рассматриваемой задачи являются: о количество грузоотправителей и грузополучателей;
о ограничения, накладываемые грузоотправителем и грузополучателем на партию груза, которая может быть отправлена и получена соответствующим субъектом; о затраты на перемещение единицы груза от каждого отправителя каждому получателю.
Классическая транспортная задача предполагает, что количество груза у отправителя точно соответствует количеству груза, необходимому получателям.
Особые виды транспортной задачи Однако в практике планирования грузовых автомобильных перевозок встречаются особые виды транспортной задачи, решение которых также может быть сведено к классической задаче:
1. Модели с несбалансированным спросом и предложением, получившие название — открытые. В таких задачах спрос может или превышать или быть меньше предложения. Если у отправителя груза больше, чем это требуется потребителю, то вводится фиктивный груэополучатель, если же спрос превышает предложение, то вводится фиктивный грузоотправитель.
2. Модель с запрещенными корреспонденциями используется, если какие-либо грузополучатели не могут получать груз от некоторых грузоотправителей. В этом случае при решении задачи между ними искусственно вводится очень большое расстояние, существенно превышающее реальное.
3. Модель с обязательными корреспонденциями используется, если какие-либо потребители должны получать груз от конкретных поставщиков. В этом случае данная корреспонденция вводится в обязательные условия.
Специальные методы решения
Для решения транспортной задачи разработаны специальные методы, позволяющие из множества возможных решений найти оптимальное. Одним из таких методов является распределительный метод, который имеет неЧ сколько разновидностей, отличающихся в основном способом выявления оптимального решения. Наиболее известны три разновидности: о метод Хичкова; о метод Креко; о модифицированный распределительный метод или ме
тод потенциалов.
Отличаются они в основном способом выявления оптимального решения. Указанные методы достаточно широко представлены в литературе по экономико-математическим методам на автомобильном транспорте.
«Поиск решения»
В настоящее время для решения транспортной задачи и задачи определения кратчайших расстояний широко применяется «Поиск решения» — встроенная возможность Microsoft Excel, позволяющая получить точное решение с наименьшими затратами времени.

В исследовании операций под транспортной задачей обычно понимают задачу выбора плана перевозок некоторого то­вара (изделий, груза) от m источников (пунктов производства, поставщиков) к n стокам (станциям назначения, пунктам сбыта), обеспечивающего минимальные транспортные затраты. При этом предполагают, что:

а) мощность i-го источника (объем поста­вок товара от i-го источника) равна S_i>0, i=l,...,m;

б) мощность j-го стока (объем поставок товара к j-му стоку) равна D_j >O, j=1,...,n;

в) стоимость перевозки единицы товара (в условных де­нежных единицах) от i-го источника к j-му стоку равна с_ij;

г) суммарная мощность всех источников равна суммарной мощно­сти всех стоков, т.е.

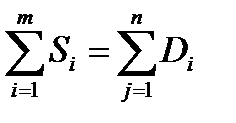(1)

Далее под объемом товара будем понимать его количество в фиксированных единицах измерения.

Для математического описания транспортной задачи вводят переменные x_ij, обозначающие объемы поставок товара от i-го ис­точника j-му стоку. В этом случае x_i1+x_i2+...+x_in — общий объ­ем поставок товара от i-го источника, т.е. мощность этого источ­ника; x_ij+x_i2+...+x_in — общий объем поставок товара к j-му стоку, т.е. мощность этого стока; c₁₁x₁₁+ c₁₂x₁₂+…+ c_mnx_mn — суммарная стоимость перевозок товара от источников к стокам. С учетом этого рассматриваемая задача может быть представлена в следующем виде:

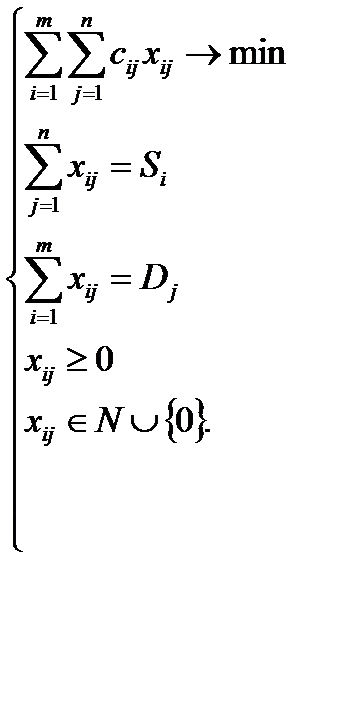(2)

На рис. 1.1-1 показано представление транспортной задачи в виде сети с m пунктами отправления и n пунктами назначения, которые показаны в виде узлов сети. Дуги, соединяющие узлы се­ти, соответствуют маршрутам, связывающим пункты отправле­ния и назначения. С дугой (i,j), соединяющей пункт отправления i с пунктом назначения j, соотносятся два вида данных: стоимость c_ij перевозки единицы груза из пункта i в пункт j и количество перевозимого груза х_ij. Объем грузов в пункте отправления i ра­вен S_i, а объем грузов в пункте назначения j равен D_j. Задача со­стоит в определении неизвестных величин x_ij, минимизирующих суммарные транспортные расходы и удовлетворяющих ограни­чениям, накладываемым на объемы грузов в пунктах отправления (предложение) и пунктах назначения (спрос).

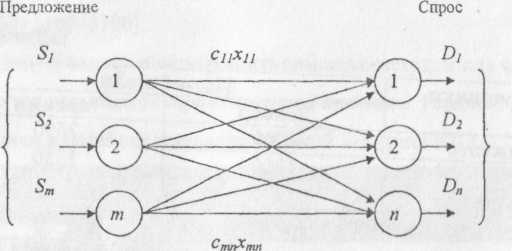
Рисунок 1.1-1 – Представление транспортной задачи в виде сети

Когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на това­ры (грузы), запрашиваемые пунктами назначения, транспортная задача называется несбалансированной. В этом случае, при ре­шении классической транспортной задачи методом потенциа­лов, применяют прием, позволяющий несбалансированную транспортную задачу сделать сбалансированной. Для этого вво­дят фиктивные пункты назначения или отправления. Выполне­ние баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.

Транспортная задача с промежуточными пунктами.

Одно практически важное обобщение классической транс­портной задачи связано с учетом возможности доставки товара от i-го источника j-му стоку по маршруту, проходящему через не­который промежуточный пункт (склад). Так, например, про­межуточные пункты являются составной частью распределитель­ной системы любой крупной компании, имеющей сеть универ­сальных магазинов во многих городах. Такая компания обычно имеет зональные оптовые базы (источники), снабжающие това­рами более мелкие региональные склады (промежуточные пунк­ты), откуда эти товары поступают в розничную торговую сеть (стоки). При этом товар для каждого фиксированного стока в об­щем случае может быть доставлен не из любого источника и по маршрутам, не обязательно проходящим через все промежуточ­ные пункты. Кроме того, промежуточные пункты могут обладать вполне определенной спецификой. Так, например, при транспор­тировке товара от источника к стоку по маршруту, проходящему через склад, часть товара может быть использована для создания неприкосновенного запаса на складе.

Задачу выбора плана перевозок товаров от источников сто­кам с учетом промежуточных пунктов, обеспечивающего мини­мальные транспортные затраты и потребности стоков, в исследовании операций называют транспортной задачей с промежу­точными пунктами. Для приобретения практических навыков в построении математических моделей таких задач обратимся к следующему примеру.

На рис. 2.1-1 представлена схема размещения складов, на ко­торой указаны: а) склады в виде узлов сети с номерами от 1 до 8; б) избыток товара на складе, который должен быть перераспре­делен в системе складов (указан в квадратных скобках рядом с узлом сети положительным числом и выражен в единицах изме­рения товара); в) недостаток товара на складе, который должен быть устранен за счет его поставок с других складов системы (указан в квадратных скобках рядом с узлом сети отрицательным числом); г) возможность перевозки товара со склада i на склад j (ориентированная дуга от круга с номером i к кругу с номером j); д) затраты, связанные с перевозкой единицы товара со склада i на склад j (величина c_ij рядом с соответствующей ориентированной дугой, выраженная в денежных единицах).

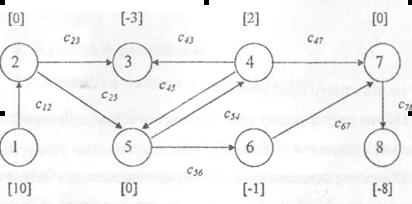
Рисунок 2.1-1

На рис. 2.1-1 видно, что суммарный избыток товара, имею­щийся на складах системы с номерами 1 и 4, равен суммарному недостатку товара, имеющемуся на складах с номерами 3, 6 и 8 той же системы. Перераспределение товара может происходить через склады с номерами 2, 4-7, которые в рассматриваемой зада­че и являются промежуточными или транзитными пунктами. Истинным пунктом отправления является лишь склад с номе­ром 1, на котором имеется избыток товара и с которого товар можно только вывозить, а истинными пунктами назначения являются склады с номерами 3 и 8, на которых есть недостаток товара, и на эти склады товары можно только завозить. Заметим также, что между складами с номерами 4 и 5 возможны перевоз­ки в обоих направлениях, но в общем случае c₄₅≠c₅₄ (например, наличие одностороннего движения по кратчайшему маршруту).

Объемы спроса и предложения, соответствующие этим пунктам отправления и назначения, вычисляются следующим образом.

Объем предложения истинного пункта отправления = объем исходного предложения.

Объем предложения транзитного пункта = объем исходно­го предложения + объем буфера.

Объем спроса истинного пункта назначения = объем исход­ного спроса.

Объем спроса транзитного пункта = объем буфера.

Объем буфера должен быть таким, чтобы вместить объем всего предложения (или спроса).

Пусть J —множество номеров складов, на которые товар может быть доставлен с k-то склада, а I — множество номеров складов, с которых товар может быть доставлен на k-й склад. T_k — величина чистого запаса товара, равная объему исходного предложения или исходного спроса. Тогда математическую мо­дель данной задачи можно представить следующим образом:

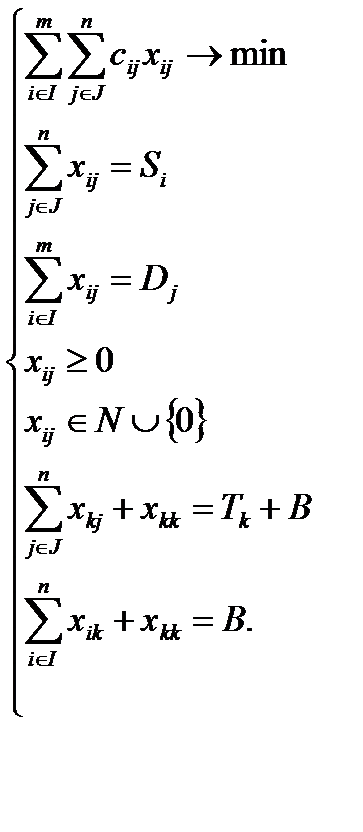(4)

Задача о назначении.

Предположим, что имеется n различных работ, каждую ко­торых может выполнить любой из n привлеченных исполнителей. Стоимость выполнения i-й работы j-ым исполнителем известна и равна с_ij (в условных денежных единицах). Необходимо распре­делить исполнителей по работам (назначить одного исполнителя на каждую работу) так, чтобы минимизировать суммарные затра­ты, связанные с выполнением всего комплекса работ.

В исследовании операций задача, сформулированная выше известна как задача о назначениях. Введем переменные х_ij, при­нимающие значение 1 в случае, когда i-ю работу выполняет i-й исполнитель и значение 0 во всех остальных случаях, ij = 1, n. Тогда ограничение

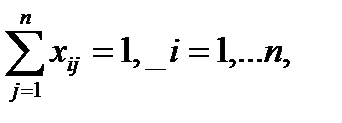
гарантирует выполнение каждой работы лишь одним исполните­лем, ограничение

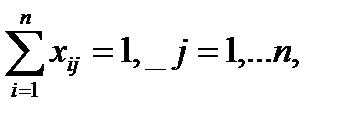
гарантирует, что каждый из исполнителей будет выполнять лишь одну работу. Стоимость выполнения всего комплекса работ равна

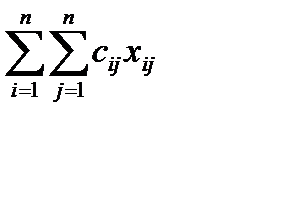
Таким образом, задачу о назначениях можно записать сле­дующим образом:

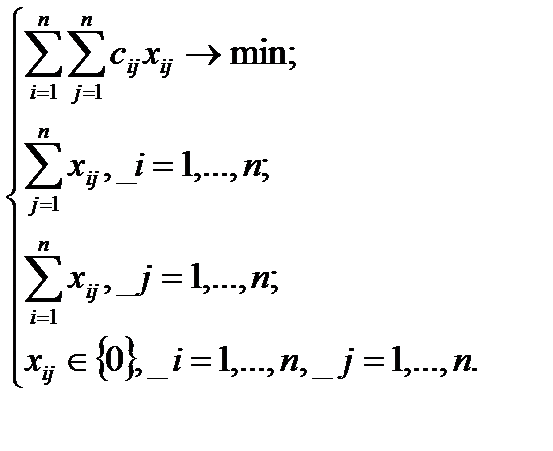
Задача о назначениях является частным случаем классиче­ской транспортной задачи, в которой надо положить n=m, S_i = 1, i = 1,...,n, D_j = 1, j = 1,...,n. При этом условие 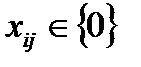, i,j = 1,...,n, означает выполнение требования целочисленности пере­менных х_ij. Это связано с тем, что мощности всех источников и стоков равны единице, откуда следует, что в допустимом цело­численном решении значениями переменных могут быть только 0 и 1.

Как частный случай классической транспортной задачи, за­дачу о назначениях можно рассматривать как задачу линейного программирования. Поэтому в данном случае используют терми­нологию и теоретические результаты линейного программирова­ния.

В задаче о назначениях переменное х_ij, может принимать значение 0 или 1. При этом в любом допустимом решении лишь и переменных могут принимать значения 1. Таким образом, любое допустимое базисное решение задачи о назначениях будет вырожденным.

На практике встречаются задачи о назначениях, в постанов­ках которых параметр c_ij для i.j = 1,...,n понимается как эффектив­ность выполнения i-й работы j-м исполнителем. В этих случаях нужно так распределить работы между исполнителями, чтобы суммарная эффективность их выполнения был бы максимальной, т.е.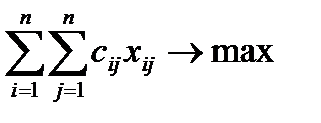

где максимум ищется при указанных выше ограничениях.

Решение задач транспортного типа с применением компьютерных программ.