Расчет железобетонных изгибаемых элементов по деформациям.
Целью расчета изгибаемого элемента по деформациям является определение его прогиба и сравнение этого прогиба с предельно допустимой нормами величиной. В основу расчета по деформациям положены следующие предпосылки: в растянутой зоне изгибаемых элементов при эксплуатации и более высоких нагрузках могут быть участки без трещин или с закрытыми трещинами (стадия I) и участки с трещинами (стадия II); наравне с упругими деформациями железобетона проявляются и неупругие; зависимость «напряжения - деформация» для бетона выражается кривой с учетом упругопластических свойств бетона;в сжатой зоне сечения имеет место прямоугольная эпюра напряжения; арматура в бетоне до и после появления трещин удлиняется иначе, чем свободный металл, бетон снижает удлинение арматуры и она получает как бы повышенный условный модуль упругости; это учитывается в расчетах введением коэффициента; на участках между трещинами сечения остаются плоскими и после прогиба элемента.
При расчете по деформациям все нагрузки принимают с коэффициентом надежности по нагрузке gf=1 (т.е. равными нормативным нагрузкам). Если прогибы ограничены технологическими или конструктивными требованиями (см. выше), то в расчет вводят постоянные, длительные и кратковременные нагрузки. Если же прогибы ограничены эстетическими требованиями, то влияние кратковременных нагрузок можно не учитывать и вводить в расчет только постоянные и длительные нагрузки.
Прогиб элемента существенно зависит от наличия трещин в растянутой зоне. Изгибаемые элементы без предварительного напряжения, как правило, работают с трещинами в растянутой зоне. Расчет по деформациям в этом случае ведется следующим образом. Прогибы определяют по обычным формулам строительной механики, в которых учитывается кривизна 1/r. Например, в середине пролета однопролетной свободно опертой балки под равномерно распределенной нагрузкой прогиб 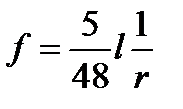 (12)
(12)
под сосредоточенным грузом прогиб такой же балки 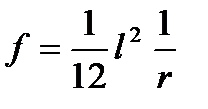 (13)
(13)
Вычисление кривизны, являющееся основной задачей расчета по деформациям, проводится по формуле 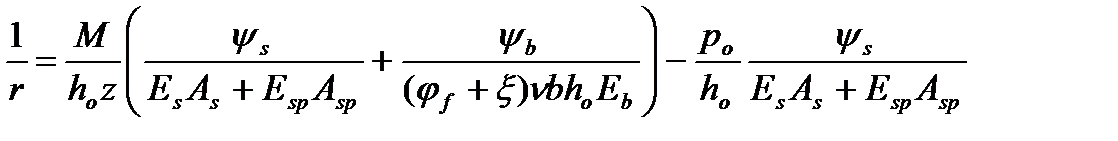 (14)
(14)
где М - изгибающий момент; z - расстояние от центра тяжести площади сечения арматуры до центра тяжести сжатой зоны сечения над трещиной, определяемое по формуле (19) (см. ниже); ys - коэффициент, учитывающий работу растянутого бетона на участке с трещинами и его сдерживающее влияние на деформации арматуры, определяемый по формуле (20); yb - коэффициент, учитывающий неравномерность распределения деформаций крайнего сжатого волокна бетона по длине участка с трещинами и принимаемый равным 0,9; jf - коэффициент формы сечения, определяемый по формуле (18); x=х/hо определяют по формуле (15); n - коэффициент, характеризующий упругопластическое состояние бетона сжатой зоны и принимаемый по табл. 11.4.
Таблица 11.4. Значения коэффициентов n и jls для тяжелого бетона
| Действие нагрузки | n | jls |
| Непродолжительное | 0,45 | 1,0 (при проволочной или гладкой стержневой арматуре); 1,1 (при стержневой арматуре периодического профиля) |
| Продолжительное: при влажности воздуха окружающей среды 40...75 % менее 40 % | 0,15 0,10 | 0,8 (при любой арматуре и влажности) |
Значение x вычисляют по формуле 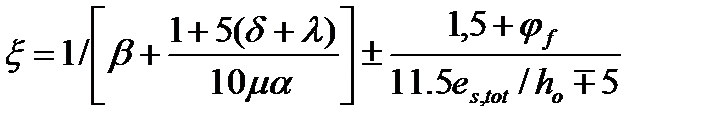 (15)
(15)
Где b - коэффициент, для тяжелого бетона b=1.8
d=M/(bh2oRb,ser) (16)
l=jf[1-hf/(2ho)] (17)
jf=[h’f(b’f-b) + a/2nA’s]/(b ho) (18)
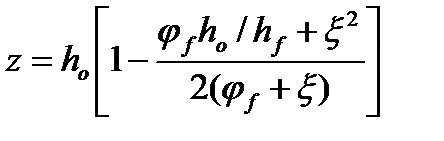 (19)
(19)
Для элементов прямоугольного сечения в формулы (15)…(19) вместо величины h’f; подставляют величины: 2a - при наличии, или нуль - при отсутствии сжатой арматуры.
Расчет сечений, имеющих полку в сжатой зоне, при x<hf/ho производят, как расчет прямоугольных сечений шириной bf. Величина коэффициента 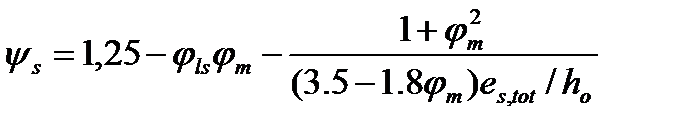 (20)
(20)
где еs,tot=|M|Ntot - расстояние от центра тяжести площади сечения растянутой арматуры до усилия предварительного обжатия (при еs,tot/hо>1,2jls); jls - коэффициент, учитывающий влияние длительности действия нагрузки и профиль арматуры и принимаемый по табл.
jm=Rbt,serWpl/|±Mr±Mrp|£1 (21)
где Wpl - момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого .бетона; для прямоугольного сечения Wpl=bh/3,5; для других сечений Wpl вычисляется с использованием табл.
Практическая методика расчета изгибаемого элемента по деформациям состоит в определении кривизны по формуле (14) с учетом формул (15)...(21), вычисления проводят несколько раз для различных видов нагрузок (постоянных, длительных, кратковременных).
Полную величину кривизны определяют по формуле
1/r=1/r1-1/r2+1/r3-1/r4 (22)
где 1/r1 - кривизна от непродолжительного действия всей нагрузки, на которую производится расчет по деформациям (см. выше); 1/r2 - кривизна от непродолжительного действия постоянных и длительных нагрузок; 1/r3 - кривизна от продолжительного действия постоянных и длительных нагрузок; 1/r4 - кривизна, вызванная выгибом элемента вследствие усадки и ползучести бетона от предварительного обжатия.
Значения 1/r1 и 1/r2 вычисляют при величинах ys иn (n - коэффициент, характеризующий упругопластическое состояние бетона сжатой зоны), соответствующих непродолжительному действию нагрузки, а 1/r3 - при ys и n, соответствующих продолжительному действию нагрузки. Если величины 1/r2 и 1/r3 оказываются отрицательными, то их следует принимать равными нулю.
Далее по формулам строительной механики, а именно (12) или (13), вычисляют прогиб и сравнивают его с требованиями норм. Если найденное значение прогиба не превосходит нормируемого, то расчет закончен; в противном случае необходимо увеличить сечение элемента или применить предварительное напряжение.
Вопрос 29
Дата добавления: 2016-05-11; просмотров: 1578;
