Меры рассеивания и зависимость между ними
67.В любых условиях стрельбы закономерность рассеивания остается неизменной, но величина площади рассеивания изменяется взависимости от выучки стреляющего, вида оружия, боеприпасов, прицельных приспособлений, положения для стрельбы, дальности стрельбы, метеорологических и других условий стрельбы.
Для измерения величины площади рассеивания, сравнения рассеивания пуль (гранат) разных видов оружия, а также для оценки рассеивания пуль (гранат) одного и того же оружия при различных условиях стрельбы могут применяться следующие меры (единицы измерения) рассеивания: срединное отклонение, сердцевинная полосаи радиус круга, вмещающего лучшую половину попаданийили все попадания.
68. Срединным отклонениемназывается такое отклонение, которое в ряду всех отклонений, выписанных по
абсолютной величине ввозрастающем или убывающем
порядке, занимает среднее место.
Срединное отклонение является основной мерой рассеивания. Оно обычно обозначается: Вд — срединное отклонение по дальности; Be — срединное отклонение по высоте; Вб — срединное отклонение по боковому направлению.
Для определения величины срединного отклонения по одному из направлений необходимо выписать все отклонения вряд ввозрастающем или убывающем порядке по абсолютной величине. Отклонение, стоящее посредине этого ряда, ибудет являться срединным отклонением.
Если ряд всех отклонений состоит из четного числа отклонений, то для определения величины срединного отклонения нужно взять два отклонения, стоящие посредине, и разделить сумму их абсолютных величин на два.
Пример. Шести пробоинам отвечают следующие величины отклонений от оси рассеивания по высоте: выше оси рассеивания + 15; +25; +70 см; ниже ее —10; —40; —60 см. Определить срединное отклонение по высоте (Вв).
Решение. Выписав по абсолютной величине все отклонения в возрастающем порядке, получим: 10; 15; 25; 40; 60; 70 см.
Вв=25+40/2 =32,5 см.
Действительно, отклонение 32,5 см больше каждого из первых трех отклонений и меньше каждого из последних трех отклонений.
Примечание. При небольшом числе измерений определение величины срединного отклонения таким способом не обеспечивает - необходимой точности, так как получение одного добавочного отклонения может значительно изменить величину срединного отклонения для одного и того же способа стрельбы.
Пример. Если к ряду отклонений, указанных в предыдущем примере, добавить еще одно отклонение, равное 80 см, то срединное отклонение станет равным 40 см (10; 15; 25; 40; 60; 70; 80).
В этих случаях величина срединного отклонения более точно • вычисляется с помощью среднего арифметического значения. Срединное отклонение равно 0,84, или округленно 5/в, среднего арифметического значения.
Среднее арифметическое значение определяется делением суммы абсолютных значений всех отклонений на количество отклонений. Так, например, по условиям предыдущего примера среднее арифметическое значение равно
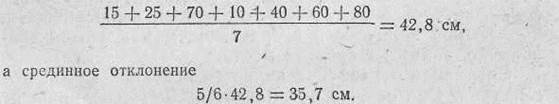
В этих случаях учитываются численные значения всех отклонений и результаты отдельных отклонений не сказываются так значительно на величине срединного отклонения.
Срединное отклонение может быть вычислено также с помощью среднего квадратического значения. Срединное отклонение равно 0,67, или округленно 2/з, среднего квадратического значения.
Среднее квадратическое значение при небольшом числе отклонений равно корню квадратному из суммы квадратов отклонений, деленной на число всех отклонений без одного.
Так, по условиям предыдущего примера среднее квадратическое значение будет равно
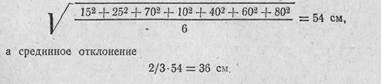
69. Если от той или иной оси рассеивания отложить в обе стороны последовательно полосы, равные по ширине соответствующему срединному отклонению, то вся площадь рассеивания окажется разделенной на восемь равных полос—по четыре в каждую сторону, а полное рассеивание по любому направлению будет равно восьми срединным отклонениям.
В действительности могут быть отклонения от центра рассеивания, превышающие четыре срединных отклонения, но вероятность получения их мала (не превышает 0,7%).
При большом числе выстрелов в каждой из полос, равной по ширине одному срединному отклонению или его части, независимо от величины рассеивания содержится определенный процент точек встречи (попаданий).
Чертеж, показывающий процентное распределение попаданий в полосы, равные по ширине одному срединному отклонению или его части, называется шкалой рассеивания(Рис.26). Шкала рассеивания в численном выражении одинакова по любому направлению и характеризует закон рассеивания.

Для полос шириной в одно срединное отклонение содержится (округленно): в первых полосах, примыкающих к оси рассеивания, по 25% точек встречи, во вторых по 16%, в третьих по 7% и в крайних по-2%.
Для полос, ширина которых равна сотой части срединного отклонения, процентное распределение попаданий указано в табл. 1 приложения 4.
70. При большом числе попаданий (точек встречи) величину срединного отклонения можно определить графическим способом (Рис.27). Для этого отсчитывают
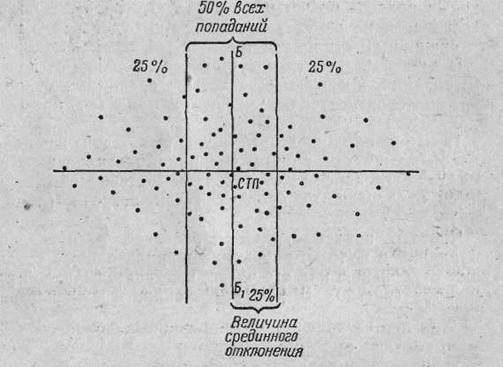
Рис. 27, Определение величины срединного отклонения по боковому направлению графическим способом справа (сверху) 25% попаданий (точек встречи) и отделяют их вертикальной (горизонтальной) линией; отсчитывают слева (снизу) 25% попаданий (точек встречи) и также отделяют их вертикальной (горизонтальной) линией. В результате этого получится полоса, вмещающая 50% попаданий (точек встречи), т. е. полоса лучшей половины попаданий.
Затем измеряют расстояние между вертикальными (горизонтальными) линиями. Половину расстояния между вертикальными (горизонтальными) линиями принимают за величину срединного отклонения. В связи с этим иногда пользуются другим определением срединного отклонения: срединным отклонением называется половина ширины центральной полосы рассеивания, вмещающей 50% всех попаданий, при условии, что ось рассеивания проходит по ее середине.
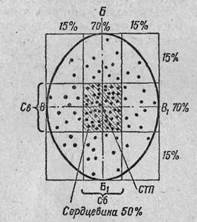
Рис. 28. Сердцевинные полосы и сердцевина рассеивания
71. Полоса рассеивания, содержащая в себе 70% попаданий (точек встречи), при условии, что ось рассеивания проходит по ее середине, называется сердцевинной сердцевина рассеивания полосой (Рис. 28).
Сердцевинные полосы обозначаются: Сд — сердцевинная полоса по дальности; Св—сердцевинная полоса по высоте; Сб — сердцевинная полоса по боковому направлению.
При пересечении двух сердцевинных полос образуется прямоугольник, включающий в себя лучшую, наиболее кучную половину всех точек встречи (0,70-0,70=0,49, округленно 0,50, или 50%).
Прямоугольник, образуемый пересечением двух сердцевинных полос, называется сердцевиной рассеивания.
Ширина сердцевинной полосы может быть определена графическим способом (Рис.29). Для этого надо отсчитать справа (сверху) 15% попаданий (точек встречи) и провести вертикальную (горизонтальную) линию; отсчитать слева (снизу) 15% попаданий (точек встречи) и также провести вертикальную (горизонтальную) линию. В результате этого вся площадь рассеивания окажется разделенной на три почти равные полосы, при этом центральная полоса содержит 70% попаданий, а крайние— по 15% каждая. Затем следует измерить расстояние между вертикальными (горизонтальными) линиями, которое и будет равно ширине сердцевинной полосы.
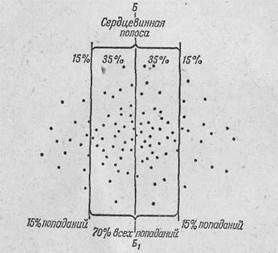
Рис. 29. Определение величины сердцевинной полосы по боковому направлению графическим способом
Между сердцевинной полосой и срединным отклонением как мерами рассеивания имеется определенная зависимость. Сердцевинная полоса включает в себя 3,06 соответствующего срединного отклонения. На практике ширину сердцевинной полосы принимают округленно равной трем срединным отклонениям.
72. При стрельбе на близкие расстояния площадь рассеивания на вертикальной плоскости имеет форму круга, что означает примерное равенство характеристик рассеивания по высоте и по боковому направлению. Поэтому о величине такого рассеивания иногда судят не по двум характеристикам (Вв и Вб или Се и Сб), а по од-
ной величине — радиусу круга, вмещающего лучшую половину (Р5о) всех попаданий или все (Рюо) попадания. Для определения величины радиуса круга, включающего 50 или 100% попаданий, необходимо (Рис.30) определить среднюю точку попадания. Затем, принимая среднюю точку попадания за центр круга, провести циркулем окружность так, чтобы она вместила половину (50%) или все (100%) точки встречи. Раствор циркуля дает в первом случае величину радиуса круга, включающего 50%. а во втором— 100% попаданий.
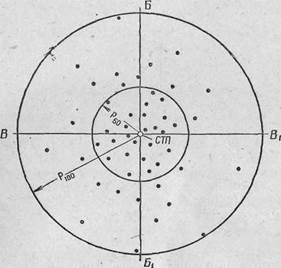
Рис. 30. Определение величины радиусов кругов, вмещающих 50 и 100% попаданий
Радиус круга, вмещающего все попадания, примерно в 2'/г раза больше радиуса круга, вмещающего лучшую половину попаданий.
Между величиной радиуса круга, вмещающего лучшую половину попаданий, срединными отклонениями и сердцевинными полосами имеется определенная зависимость. Радиус круга, вмещающего лучшую половину паданий (50%), равен 1,76 срединного отклонения или 0,6сердцевинной полосы.
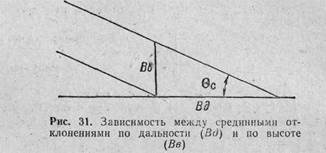
73. Между величинами рассеивания по дальности ипо высоте имеется определенная зависимость: рассеивание по дальности равно рассеиванию по высоте, умноженному на 1000и разделенному на величину угла падения в тысячных (Рис. 31), т. е.
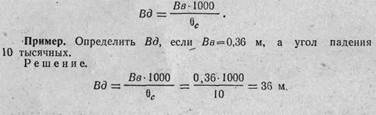
Дата добавления: 2017-02-04; просмотров: 1823;
