Гидравлический расчет кольцевой сети

В кольцевой сети при заданной ее конфигурации и известных узловых расходах (отборах воды из сети) можно наметить бесконечное количество вариантов распределения потоков воды, удовлетворяющих заданному водопотреблению. Каждому из этих вариантов потокораспределения будут соответствовать определенные диаметры труб, а изменения диаметра хотя бы одного участка повлечет за собой изменения расходов на всех участках сети, таким образом задача сводится к совместному определению и расходов и диаметров на всех участках сети.

Общее математическое решение задачи сводится к решению системы уравнений в которой число неизвестных в 2 раза больше числа участков. В систему уравнений входят уравнения двух типов:

1. Уравнение баланса потерь напора в кольцах по второму закону Киргоффа.

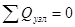
2. Уравнение по первому закону Кирхгоффа .

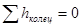
Число уравнений первого типа равно числу узлов. Число уравнений второго типа равно числу колец, что в сумме меньше чем удвоенное число участков.

n _узл + n _колец < 2n_{участков}

Такая система уравнений не имеет решения в общем виде (является неопределенной) и для ее решения нужно задаться дополнительными условиями: либо расходами, либо диаметрами (т.е. уменьшить количество неизвестных в 2 раза). В практических расчетах поступают следующим образом: обоснованно производят начальное потокораспределение в кольцах сети с выполнением первого закона Кирхгоффа ( 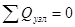). По полученным расходам на участках назначают их экономичные диаметры, затем производят перераспределение потоков при известных диаметрах с тем, чтобы добиться выполнения также и второго закона Кирхгоффа ( 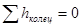). Этот поверочный расчет называется увязкой сети.

Увязка сети

где S- гидравлическая характеристика участка

А- гидравлическая характеристика трубы

l- длина трубы

Конечно, при начальном потокораспределении не удалось добиться выполнения второго закона Кирхгоффа, и сумма потерь напора в кольцах равна не 0, а какому-то значению ∆ h.

∆ h_I = s₁q₁²+ s₂q₂²- s₄q₄²- s₃q₃²

«-« против часовой стрелки

«+» по часовой стрелке

∆ h_II = s₃q₃² + s₅q₅² – s₇q₇² – s₆q₆²

чтобы добиться выполнения второго закона Кирхгоффа нужно ввести поправочные расходы ∆q в кольцах в направлении противоположном направлению невязки, т.е. где надо уменьшить и увеличить.

S₁(q₁- ∆q_I)² + S₂(q₂- ∆q_I)² – S₄(q₄+∆q_I)²- S₃(q₃+∆q_I- ∆q_II)² = 0

Для второго кольца

S₃(q₃-∆q_II+∆q_I)² + S₅(q₅-∆q_II)² – S₇(q₇+∆q_II)²- S₆(q₆+∆q_II)²=0

Эта система уравнений с двумя неизвестными ∆q_I и ∆q_II которая имеет в принципе математическое решение, которое достаточно сложное. В реальных инженерных расчетах каждое кольцо рассматривается самостоятельно, независимо от примыкающих колец, т.е. из каждого уравнения выбрасываются члены, содержащие ∆ q примыкающих колец, выбрасываются члены, содержащие ∆q² , как имеющие сравнительно очень малую величину.

В результате решения этой системы при таких допущениях получим:

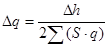
где 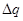-поправочный расход для данного кольца;

∆h – невязка, полученная в результате гидравлического расчета при начальном потокораспределении в данном кольце.

S – гидравлические характеристики

q – расходы по участкам при первоначальном потокораспределении.

Так как математическая задача решена очень грубо, после учета поправочного расхода ∆ q второй закон Кирхгоффа выполнен не будет, и в кольце все равно останется невязка, но конечно, меньше предыдущей.

В инженерных расчетах принято считать допустимой невязку в кольцах 0,5 м. Если полученные невязки больше 0,5, цикл расчетов повторяется несколько раз, пока не доберемся до 0,5 м.