Определение податливости и жесткости П-образного компенсатора.

На рисунке 42 изображена схема П-образного компенсатора. Необходимо определить его податливость 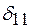и жесткость .

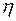Конструкция компенсатора представляет собой систему, состоящую из круговых отводов и прямолинейных участков труб.

По определению податливостью компенсатора 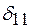в заданной точке и в заданном направлении является перемещение от единичной силы 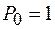, в этом направлении.

Компенсатор П-образной формы на расчетной схеме рассматривается , как стержневая система, состоящая из круговых (1, 3-ий) и прямолинейных (2, 4-ый) участков).

Для определения перемещения 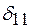используем известный из курса сопротивления материалов метод Мора (10.2). Интеграл Мора для П-образного компенсатора примет вид

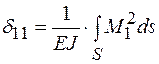, (10.3)

где 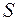- суммарная длина всех участков, прямолинейных и круговых;

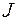- осевой момент инерции сечения трубы, определяемый по формуле

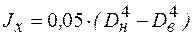. (10.4)

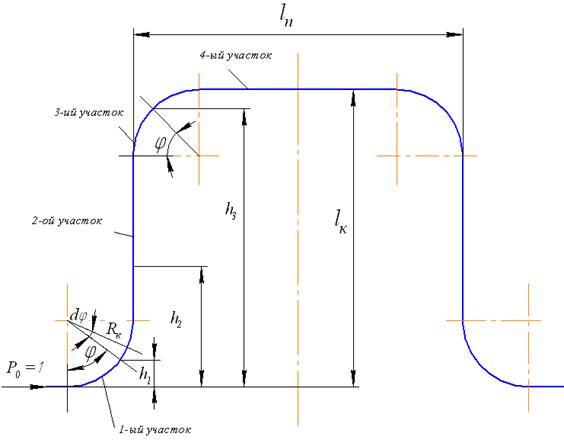
Рисунок 42. Расчетная схема П-образного компенсатора.

С учетом симметрии компенсатора получается следующее выражение для его податливости

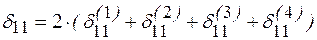, (10.5)

где 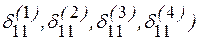- определенные интегралы, вычисленные на соответствующих участках.

Рассмотрим, как вычисляется определенный интеграл на первом участке. Изгибающий момент 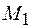в поперечных сечениях кругового участка компенсатора от единичной силы вычисляется, как произведение единичной силы на плечо 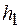(рисунок 42).

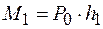(10.6)

Для кругового участка компенсатора удобнее перейти к полярным координатам, тогда

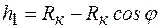, (10.7)

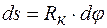. (10.8)

После этого получаем интеграл

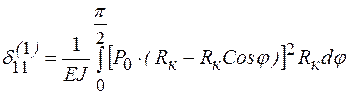. (10.9)

После интегрирования получаем следующий результат

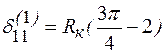. (10.10)

Для второго участка

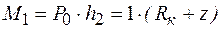
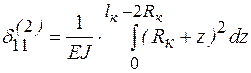. (10.11)

Для третьего участка

.

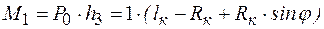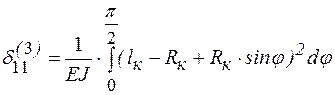. (10.12)

Для половины четвертого участка

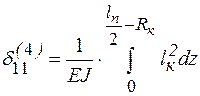. (10.13)

Полученные выражения нужно умножить на 2, чтобы получить полную податливость компенсатора. Однако, прежде чем это делать, необходимо отметить важную особенность, которая возникает в изогнутой части трубы компенсатора. Здесь возникает более сложное напряженной состояние, чем в обычном круговом стержне. В классической теории расчета изогнутых стержней положена гипотеза о неизменности формы поперечного сечения стержня при изгибе. В данном же случае (расчет отводов при изгибе) форма поперечного сечения изменяется под действием возникающих сил (рисунок 43).

Рассмотрим элемент круговой трубы (отвода), изображенный на рисунке 43. На выпуклой стороне отвода возникают растягивающие напряжения, а на вогнутой – сжимающие напряжения. Равнодействующие силы Т направлены к нейтральной оси отвода и вызывают сплющивание поперечного сечения отвода при изгибе.

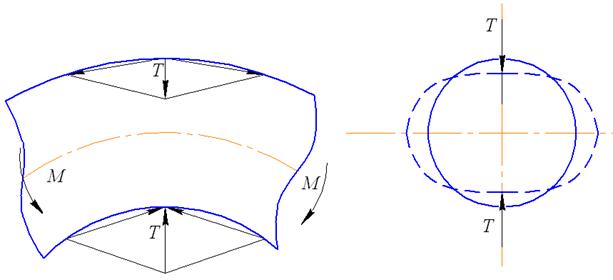
Рисунок 43. Схема деформации отвода при изгибе.

В связи с этим для получения более точного решения вводят коэффициент снижения жесткости отводов при изгибе .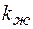

Для стальных отводов, при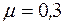

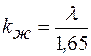, (10.14)

где - коэффициент изогнутой трубы, геометрическая характеристика отвода

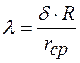; (10.15)

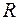– радиус изгиба отвода;

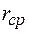– средний радиус кольцевого сечения отвода.

Таким образом, после введения коэффициента жесткости отводов и суммирования результатов интегрирования на всех участках получается выражение для вычисления податливости П-образного компенсатора

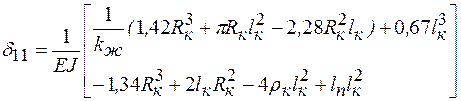(10.16) Для того, чтобы определить податливость Z-образного компенсатора (рисунок 44,а) необходимо рассмотреть только первые три участка П-образного компенсатора (рисунок 42).

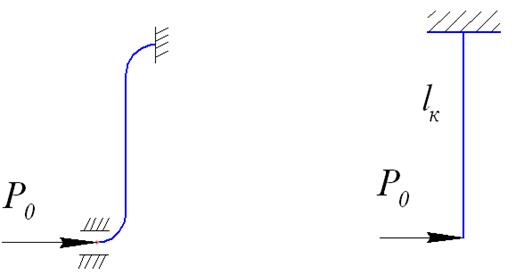
Рисунок 44. Расчетные схемы Z и Г-образного компенсатора.

После суммирования интегралов на первых трех участках получаем

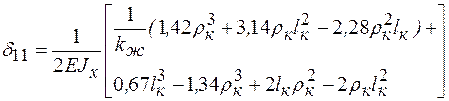(10.17)

Податливость Г-образного компенсатора получается в результате анализа справочных формул для определения поперечных перемещений прямого стержня

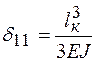. (10.18)