Определение продольных перемещений подземного трубопровода при отсутствии участка предельного равновесия грунта.

Далее рассматривается второй случай расчетной схемы подземного трубопровода (рисунок 37), когда участок предельного равновесия грунта отсутствует, т.е. выполняется условие, при котором критерий (9.46) меньше единицы

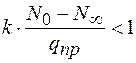(9.53)

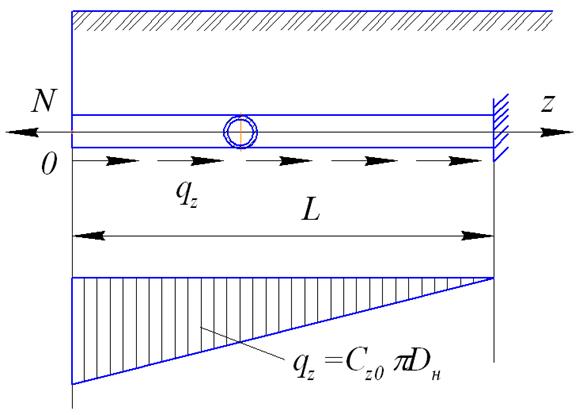
Рисунок 37. Расчетная схема трубопровода при отсутствии участка предельного равновесия грунта

В начале трубопровода вдоль его оси приложена сила 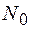, а сопротивление грунта линейно зависит от величины продольных перемещений поперечных сечений трубы (рисунок 37)

.

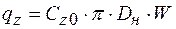Таким образом, рассматриваемая расчетная схема соответствует расчетной схеме второго участка предыдущей задачи. Поэтому уравнения для продольных перемещений 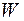и продольной силы будут аналогичны уравнениям (9.22) и (9.23).

Продольные перемещения трубопровода

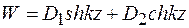, (9.54)

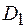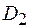где и - постоянные интегрирования.

Продольная сила

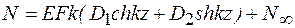. (9.55)

Произвольные постоянные 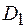и 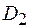определяются из граничных условий. Первое граничное условие

при , .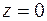

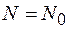С учетом гиперболических функци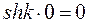й,

и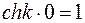

из уравнения (9.49) получаем условие

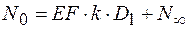, откуда

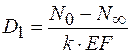. (9.56)

Второе граничное условие

при .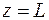

Из уравнения (9.48) получаем условие

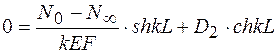, откуда

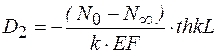(9.57)

После того, как постоянные интегрирования определены можно найти продольное перемещение в начале трубопровода 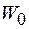и продольную силу на конце участка .

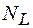Перемещение в начале трубопровода определяется из условия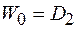

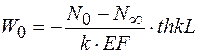. (9.58) После подстановки постоянных интегрирования 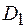и 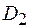в уравнение (9.49) при 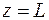получаем выражение для продольной силы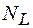

,

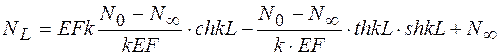которое после упрощения с учетом известного соотношения для гиперболических функций

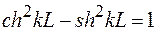
принимает окончательный вид

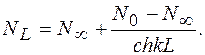(9.59)

Для определения длины участка магистрального трубопровода 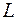используем тот же критерий (9.40), что и в предыдущей задаче

.

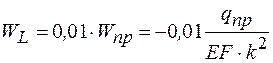В результате получаем выражение

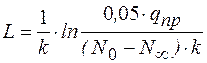. (9.60)

Полученные решения позволяют рассмотреть ряд практически важных задач.