Выбор толщины стенки магистрального трубопровода.

Как было сказано выше, для подземного магистрального трубопровода в качестве предельного состояния принято условие разрушения материала трубы, характеризуемое расчетным сопротивлением .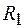

Поскольку в стенке трубы возникает двухосное напряженное состояние, характеризуемое кольцевым 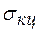и продольным 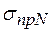напряжениями, максимальные напряжения в условие прочности (8.30) должны определяться по эквивалентным напряжениям.

Согласно СНиП 2.05.06-85 эквивалентные напряжения определяются по IV теории прочности (критерий удельной потенциальной энергии формоизменения – энергетическая теория прочности)

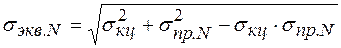(8.46)

При отсутствии продольных напряжений 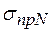или в случае, когда знак кольцевых 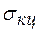и продольных напряжений 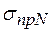совпадает, толщину стенки трубопровода определяют из условия

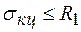(8.47)

Подставляя в формулу (8.35) вместо внутреннего диаметра его выражение через наружный диаметр стенки 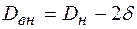получаем выражение для условия прочности

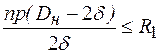(8.48)

и формулу для определения толщины стенки трубопровода из расчета по кольцевым напряжениям

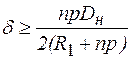. (8.49)

При наличии сжимающих продольных напряжений предельное состояние принимает следующий вид

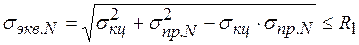. (8.50)

Если учесть тот факт, что данное условие выполняется только при отрицательных продольных напряжениях, тогда можно подставить знак минус перед продольными напряжениями 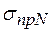и в дальнейшем знак не учитывать.

После этого выполняем ряд алгебраических действий

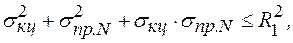
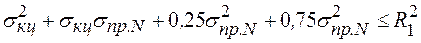
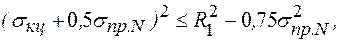
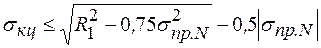или

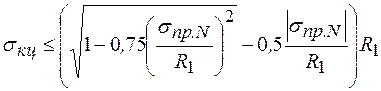
Выражения в скобках есть коэффициент, учитывающий двухосное напряженное состояние труб магистрального трубопровода

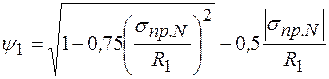. (8.51)

Тогда предельное состояние с учетом двухосности напряженного состояния примет следующий вид

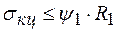, (8.52)

а толщина стенки трубы будет определяться по формуле

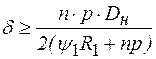. (8.53)

Если необходимо учитывать продольные осевые напряжения 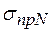, то расчет толщины стенки трубы 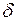проводят методом последовательных приближений. Вначале задаются ориентировочным значением толщины стенки 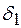, вычисленным только по кольцевым напряжениям, затем с учетом этой величины определяют продольные напряжения 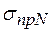, далее коэффициент 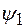и толщину стенки 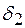. После этого проверяют условие

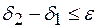, (8.54)

где 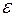- наперед заданная малая величина, удовлетворяющая точности расчета.

Если условие не выполняется, то расчет повторяют с 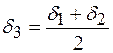и т.д., пока не выполнится условие (8.54).