Проверка прочности трубопровода.

После определения толщины стенки и продольных напряжений по формуле (8.41), осуществляют проверку прочности трубопровода по формуле

,

где 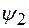- коэффициент, учитывающий двухосное напряженное состояние металла труб, при растягивающих осевых продольных напряжениях 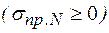принимаемый равным единице, при сжимающих 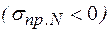определяемый по формуле

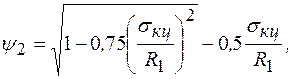(8.55)

.

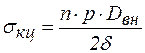Если необходимо ограничить (предотвратить) недопустимые пластические деформации подземного и наземного в насыпи трубопровода проверку проводят по второму предельному состоянию, по которому деформации трубы ограничены нормативным пределом текучести 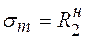. В этом случае проверку проводят по условиям

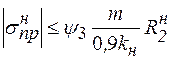(8.56)

(8.57)

где 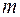– коэффициент условий работы трубопровода;

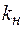– коэффициент надежности по назначению;

– нормативное расчетное сопротивление, значение которого равно пределу текучести стали 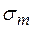для труб по ГОСТ и ТУ;

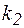=0,9 – коэффициент надежности по материалу (СНиП 2.05.06-85);

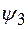- коэффициент, учитывающий двухосное напряженное состояние металла труб; при растягивающих продольных напряжениях принимаемый равным единице, при сжимающих 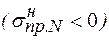- определяемый по формуле

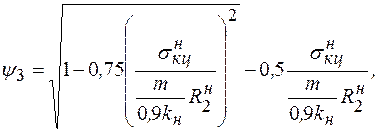(8.58)

где ;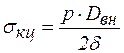

– максимальное суммарное продольное напряжение от нормативных нагрузок и воздействий.

Выполнение этих условий обеспечивает местную устойчивость стенок трубы и не допускает накопление пластических деформаций (обеспечивается долговечность).

Необходимо отметить, что по второму предельному состоянию продольные напряжения определяются с учетом изгиба трубопровода для крайних волокон сечений трубы, исходя из упругой работы металла.

В СНиП 2.05.06-85 приведена формула для определения максимальных продольных напряжений для частного случая упругого изгиба трубы, при воздействии внутреннего давления p и температурного перепада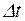

(8.59)

где 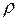– минимальный радиус изгиба оси трубы.

В формуле (8.59) третье слагаемое соответствует выражению для напряжений в поперечном сечении трубы при упругом изгибе (8.10).

9. Продольные перемещения подземного трубопровода.

Подземные магистральные трубопроводы рассчитывают в зависимости от характеристик среды, в которой они находятся при эксплуатации. Эти характеристики определяются на основе инженерных изысканий трассы.

9.1. Деформации в прямых стержнях при растяжении – сжатии.

Математическая модель стержня при растяжении содержит: уравнение равновесия, геометрические соотношения Коши и физические соотношения, выражаемые законом Гука.

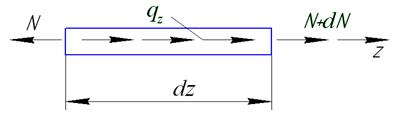
Рисунок 30. Схема нагружения элемента стержня при растяжении.

· Уравнение равновесия элемента стержня в проекциях сил на ось z

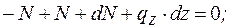(9.1)

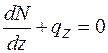, (9.2)

где 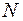– продольная сила;

- погонная продольная нагрузка.

· Геометрическое соотношение. Формула Коши. В соответствии с гипотезой плоских сечений перемещение плоского сечения перпендикулярного оси является функцией одной переменной 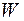(рисунок 31) . Формула Коши устанавливает дифференциальную зависимость между продольными перемещениями стержня 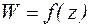и относительной линейной деформацией

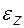
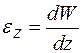. (9.3)

· Физические зависимости. Закон Гука при одноосном напряженном состоянии

, (9.4)

где 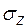- нормальные напряжения в поперечном сечении стержня.

При равномерном распределении напряжений в поперечном сечении получаем продольную силу

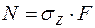, (9.5)

где 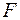– площадь поперечного сечения стержня.

После последовательной подстановки в уравнение (9.5) выражений (9.4) и (9.3)

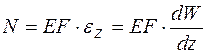, (9.6)

и с учетом (9.2) получается математическая модель прямого стержня при растяжении - сжатии

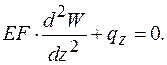(9.7)

Продольные перемещения 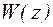находятся двукратным интегрированием выражения (9.7)

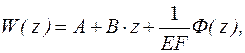(9.8)

где нагрузочная функция, зависящая от заданной нагрузк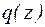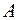и ;

и 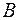– постоянные интегрирования определяемые из граничных условий.

Если стержень находится в линейноупругой среде, препятствующей продольным перемещениям прямого стержня и имеющей жесткость , то сопротивление среды будет пропорционально продольным перемещениям 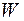и направлено против этих перемещений

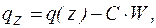(9.9)

а дифференциальное уравнение (9.7) принимает вид

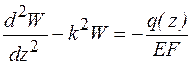, (9.10)

где .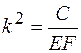

Такая математическая модель может быть использована для определения продольных перемещений магистрального трубопровода в случае линейной модели грунта. Однако, исследования показали, что она применима только для малых перемещений, а для больших перемещений существует нелинейная зависимость между сопротивлением грунта 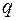и продольными перемещениями .

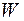Чтобы повысить точность расчетов на практике применяют нелинейную модель, которая отражает реальные свойства грунта.