Идеальное интегрирующее.

Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины:

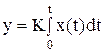; W(s) =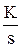

При подаче на вход звена ступенчатого воздействия x(t) = 1 выходной сигнал постоянно возрастает (см. рисунок 4.2):

h(t) = K^.t.

Это звено астатическое, т.е. не имеет установившегося режима.

Примером такого звена может служить емкость, наполняемая жидкостью. Входной параметр – расход поступающей жидкости, выходной - уровень. Изначально емкость пуста и при отсутствии расхода уровень равен нулю, но если включить подачу жидкости, уровень начинает равномерно увеличиваться.

2.2) Реальное интегрирующее.

Передаточная функция этого звена имеет вид

W(s) = .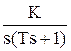

Переходная характеристика в отличие от идеального звена является кривой (см. рис. 4.2):

h(t) = K^.(t – T) + K^.T^.e ^-t/T.

Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора. Если напряжение на двигатель не подается, то ротор не двигается и угол его поворота можно принять равным нулю. При подаче напряжения ротор начинает раскручиваться, а угол его поворота сначала медленно вследствие инерции, а затем быстрее увеличиваться до достижения определенной скорости вращения.

Дифференцирующее.

3.1) Идеальное дифференцирующее.

Выходная величина пропорциональна производной по времени от входной:

; W(s) = K*s

При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию): h(t) = K^.d(t).