Детерминдік сигналдарды көрсетудің жиіліктік түрі
Бұл жағдайда базистік функция ретінде келесі функциялар алынған:
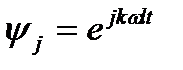 (4.6)
(4.6)
(мұндай функциялар уақыт бойынша инвариантты сызықтық жүйелерді талдауда маңызды). 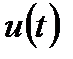 периодтық сигналы үшін
периодтық сигналы үшін 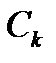 коэффициенті базистік функциялар үшін спектр деп аталынады және келесідей анықталады:
коэффициенті базистік функциялар үшін спектр деп аталынады және келесідей анықталады:
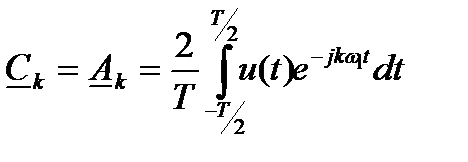 , (4.7)
, (4.7)
мұндағы 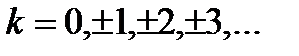
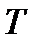 -сигнал периоды,
-сигнал периоды, 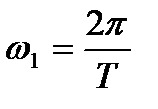
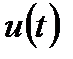 периодтық сигналын (4.6) базистік функцияның көмегімен көрсету, комплексті түрде Фурье қатарына жіктеу деп аталынады және келесі түрде өрнектеледі:
периодтық сигналын (4.6) базистік функцияның көмегімен көрсету, комплексті түрде Фурье қатарына жіктеу деп аталынады және келесі түрде өрнектеледі:
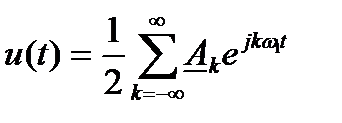
Фурье қатарын тригонометриялық түрге жіктеу келесі түрде өрнектеледі:
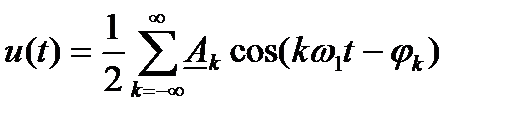 немесе
немесе
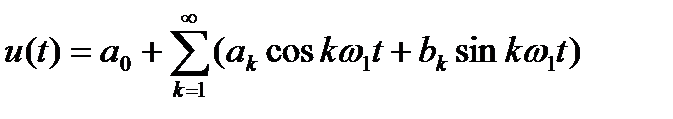 ,
,
мұндағы 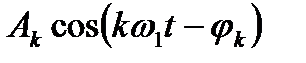 – k-сыншы гармоникалық құрамдасы,
– k-сыншы гармоникалық құрамдасы, 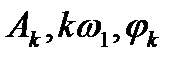 k-сыншы гармоникалық құрамдастың амплитудасы, жиілігі және бастапқы фазасы;
k-сыншы гармоникалық құрамдастың амплитудасы, жиілігі және бастапқы фазасы;
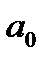 – тұрақты құрамдасы, ол сигналдың период ішінде, сигналдың орташа мәнін өрнектейді:
– тұрақты құрамдасы, ол сигналдың период ішінде, сигналдың орташа мәнін өрнектейді:
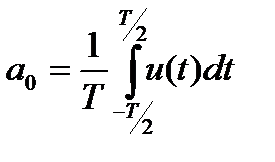 ,
, 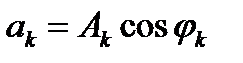 ,
, 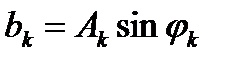 ,
, 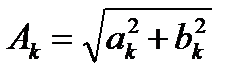 ,
,
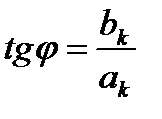 ,
, 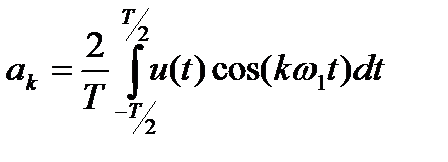 ,
, 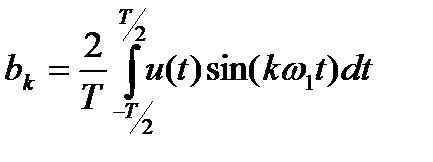 .
.
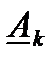 –
– 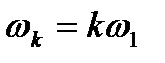 жиіліктің гармоникалық құрамдасының комплексті амплитудасы
жиіліктің гармоникалық құрамдасының комплексті амплитудасы 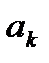 және
және 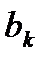 коэффициенттері келесі түрде байланысқан:
коэффициенттері келесі түрде байланысқан: 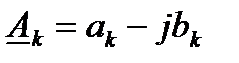 .
.
Үздіктілік (дискреттілік) – спектрлі периодты сигналдардың ерекшелігі болып табылады. Көршілес спектральды желістер арасындағы арақашықтықтар бірдей және негізгі гармоникалық жиілікке тең.
Периодты емес сигналды, өзгеру периоды шексіздікке тең болатын периодты сигнал ретінде қарастыруға болады. 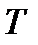 периоды үлкейгенде, сигнал спектрінде және спектральді құрамдас амплитудалардағы аралас жиіліктер арасындағы интервал кішірейеді және
периоды үлкейгенде, сигнал спектрінде және спектральді құрамдас амплитудалардағы аралас жиіліктер арасындағы интервал кішірейеді және 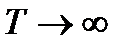 шек те өте кіші шексіз шамаға айналады. Бұл жағдайда периодты сигналды спектральді жіктелуін бейнелейтін Фурье қатары, периодты емес сигналдың спектральді жіктелуін бейнелейтін Фурье интегралына түрленеді:
шек те өте кіші шексіз шамаға айналады. Бұл жағдайда периодты сигналды спектральді жіктелуін бейнелейтін Фурье қатары, периодты емес сигналдың спектральді жіктелуін бейнелейтін Фурье интегралына түрленеді:
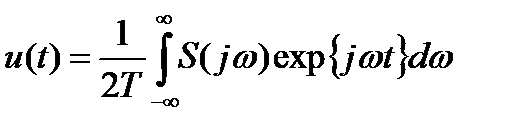 (4.8)
(4.8)
мұндағы
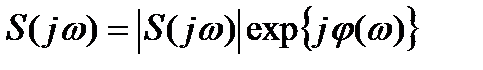 – спектральді тығыздық,
– спектральді тығыздық,
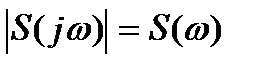 – сигналдың амплитудалық-жиіліктік сипаттамасы,
– сигналдың амплитудалық-жиіліктік сипаттамасы,
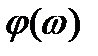 – сигналдың фаза-жиіліктік сипаттамасы.
– сигналдың фаза-жиіліктік сипаттамасы.
(4.8) өрнек Фурьенің кері түрлену формуласы деп аталынады.
Спектрлі тығыздық сигналдың уақытша функциясымен, Фурьенің кері түрленуі арқылы байланысты
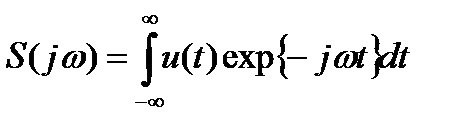
Спектрлі тығыздық периодты емес сигналды бейнелейді және келесі шарттарды қанағаттандырады:
1. 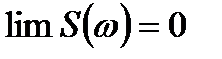
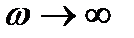
2. Спектрлі тығыздықтың модулі жұп, ал аргументі – тақ жиіліктік функция болып табылады, яғни:
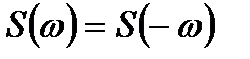
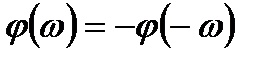
Дата добавления: 2016-04-22; просмотров: 2225;
