Физическое обоснование эксперимента. Пусть кусок льда массой m1 при температуре 0°С погружают в калориметр с водой, масса которой m2 и температура t0°С.

Пусть кусок льда массой m₁ при температуре 0°С погружают в калориметр с водой, масса которой m₂ и температура t₀°С.

Плавление льда и нагревание полученной из него воды происходит за счет охлаждения калориметра с водой, в результате чего температура смеси (исходной воды и растаявшего льда) в калориметре понижается до t₁°С.

Пусть масса калориметра m_к, масса мешалки m_м, общая их масса m₃ =m_к + m_м. Теплоемкость латуни, из которой сделаны калориметр и мешалка c₂ =386 Дж/(кг К), теплоемкость воды –c₁ = 4190 Дж/(кг К).

Закон сохранения энергии в виде уравнения теплового баланса в этом случае запишется так:

.

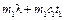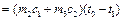(12.1)

Отсюда

.

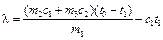(12.2)

Полное изменение энтропии S₂ - S₁ при переходе тела из состояния I в состояние 2 равно сумме приведенных теплот, соответствующих этому переходу

.

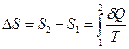(12.3)

Это изменение энтропии будет складываться из приращения энтропии при плавлении льда массы m₁ при температуре плавления Т_пл =273,15 К

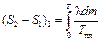
(12.4)

и приращения энтропии при дальнейшем нагревании массы m₁, получившейся изо льда воды от Т_пл до Т₁ = (273,15 + t₁) K:

.

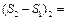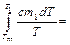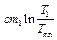(12.5)

Таким образом, полное изменение энтропии в процессе плавления льда и нагревания получившейся из него воды будет равно

.

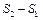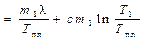(12.6)

Уравнение (12.2) справедливо, если отсутствует теплообмен с окружающей средой, что обеспечивается либо в условиях идеальной теплоизоляции системы, либо при бесконечно быстром таянии льда. Однако в действительности эти условия не выполняются. Поэтому необходимо учитывать теплообмен с окружающей средой.

Графический метод учета теплообмена с окружающей средой, описываемый ниже, дает исправленные значения температуры t₀'и t₁' . Уравнение (12.2) с учетом теплообмена примет вид

.

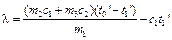(12.7)