Расчеты продольных перемещений подземных трубопроводов
В процессе эксплуатации подземные трубопроводы под действием продольных усилий, вызванных внутренним давлением и перепадом температур, могут перемещаться в грунте, особенно у мест выхода на поверхность.
Грунт оказывает сопротивление перемещением в форме касательных напряжений по контакту труба-грунт. При малых перемещениях связь между трубой и грунтом упругая, касательные напряжения tх в сечении х трубопровода линейно зависят от перемещений в том же сечении Uх
 ,
,
где kи – коэффициент постели грунта при продольных перемещениях, некоторые значения которого для ориентировочных расчетов приведены в табл. 6.3.
| |
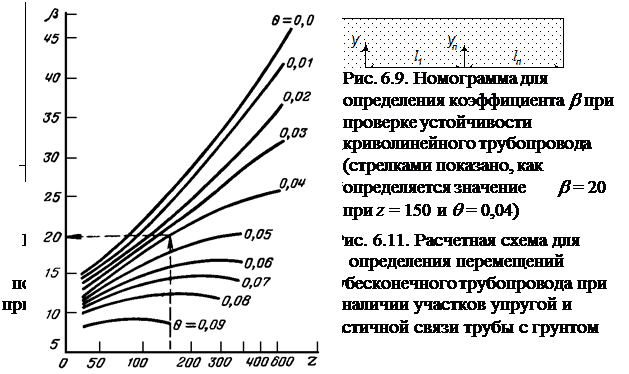
Р
Расчетная схема приведена на рис. 6.10, 6.11. Эквивалентное продольное усилие Р0, т.е. усилие, которое может быть реализовано в продольные перемещения,
 . (6.69)
. (6.69)
Продольные перемещения Uх, касательные напряжения tх и продольные усилия Рх в сечении х рассматриваемого участка трубопровода длиной l1 определяются по формулам
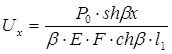 ; (6.70)
; (6.70)
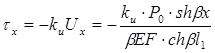 ; (6.71)
; (6.71)
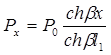 , (6.72)
, (6.72)
где b – параметр,
 ; (6.73)
; (6.73)
sh bx,ch bx – функции гиперболических синуса и косинуса,
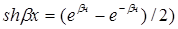 , (6.74)
, (6.74)
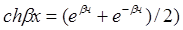 . (6.75)
. (6.75)
Таблица 6.3
Значение коэффициента постели грунта при продольных
перемещениях
| Грунт | Kи, МН/м3 | Грунт | Kи, МН/м3 |
| Песок средней плотности Супесь Суглинок Глина тугопластичная | Глина мягкопластичная Торф сухой Торф влажный | 1,5 0,5 1,0 |
Длина участка l1, в пределах которого имеют место продольные перемещения, с точностью до 6 % определяются из соотношения
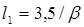 . (6.76)
. (6.76)
Максимальные перемещения Umax и касательные напряжения tmax имеют место в конце участка l1
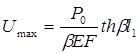 ; (6.77)
; (6.77)
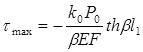 . (6.78)
. (6.78)
Расчетная схема и соответствующие ей зависимости действительны, если усилие Р0 не превышает предельного Рпр
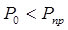 , (6.79)
, (6.79)
которое определяют по формуле
 , (6.80)
, (6.80)
где tпр – продольные касательные напряжения, определяемые по формулам (6.60), (6.61) и (6.62), в которых коэффициенты надежности по нагрузке пгр = 1,2, пс.в = 1,1 для определения qм и qиз и пс.в = 1,0 для расчета qпр.
При этом максимальные перемещения Umax в точке х = l1
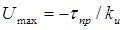 , (6.81)
, (6.81)
а максимальные касательные напряжения tmax, в той же точке равны предельным:
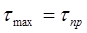 . (6.82)
. (6.82)
Если усилие Р0 превышает Рпр, продольные перемещения столь значительны, что связь между трубой и грунтом из упругой переходит в пластичную, при которой касательные напряжения по контакту труба-грунт не зависят от значения продольных перемещений и равны tпр. Таким образом, отрезок трубопровода, вовлеченный в перемещения, увеличивается, и в его пределах, наряду с участком упругой связи трубопровода с грунтом l1 формируется участок пластичной связи lп (рис. 6.10).
На участке упругой связи распределение Uх, tх и Рх рассчитываются по формулам (6.70), (6.71), (6.72) с заменой величины Р0 на Рпр.
Длина участка пластичной связи трубопровода с грунтом определяется по формуле
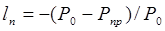 , (6.83)
, (6.83)
где величина р0 находится из выражения (6.59) с учетом отрицательного значения касательных напряжений, принятого в расчете продольных перемещений.
Продольные усилия по длине трубопровода на участке lп изменяются по следующей зависимости:
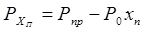 . (6.84)
. (6.84)
Продольные перемещения на участке lп с учетом смещения на участке l1 можно определить из выражения
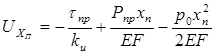 . (6.85)
. (6.85)
Перемещение конечного сечения трубопровода
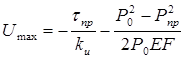 . (6.86)
. (6.86)
Пример. Определить полное перемещение свободного конца рассматриваемого отрезка трубопровода, построив эпюры распределения перемещений, касательных напряжений и продольных усилий по длине трубопровода.
Исходные данные: Dн = 1,02 м; d = 14,3 мм; F = 0,045 м2; sкц = 286 МПа; Р0 = 8,244 МН; gгр = 16 кН/м3; jгр = 36°; сгр= 0; kц = 8,0 МН/м3; h0 = 1,0 м; 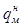 = 3536 Н/м;
= 3536 Н/м; 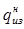 = 45 Н/м;
= 45 Н/м; 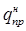 = 780 Н/м.
= 780 Н/м.
Определяем нагрузку от собственного веса трубопровода с учетом коэффициентов надежности по нагрузке пс.в = 1,1 для расчета qм и qиз и пс.в = 1,0 для расчета qпр.
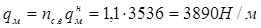 ;
;
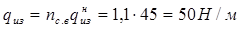 ;
;
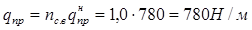 ;
;
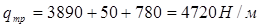 .
.
Подсчитываем по формуле (6.61) среднее удельное давление на единицу поверхности и контакта трубы с грунтом с учетом коэффициента пгр= 1,2
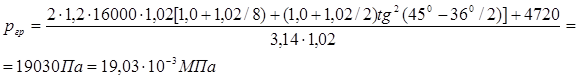
далее по формуле (6.60) определяем предельные касательные напряжения (с учетом того, что в данном расчете касательные напряжения отрицательны)
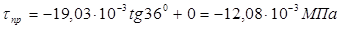 ,
,
и по формуле (6.59) р0
 .
.
Для уточнения расчетной схемы подсчитаем предельное усилие

Сопоставив величины усилий Р0 и Рпр 8,244 > 0,742 МН, делаем вывод, что данный пример соответствует расчетной схеме (см. рис. 6.10), согласно которой рассматриваемый отрезок трубопровода включает участок упругой связи трубы с фунтом и пластичной связи. Длина участка упругой связи по формуле (6.76)
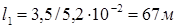
соответственно b l1 = 3,5; ch b l1 = 16,5.
Определимперемещения, касательные напряжения и продольные усилия в несколькихсечениях участка l1, заменив в формулах (6.70), (6.71) и (6.72)значение Р0на Рпр.
При х = 0, Ux = 0, tх = 0
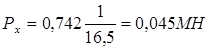 .
.
При х = 10 м
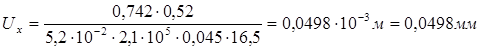 ;
;
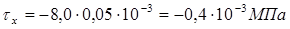 ;
;
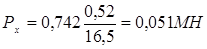 .
.
Результаты вычислений для остальных сечений занесены в табл. 6.4.
Длина участка пластичной связи трубопровода с грунтом по формуле
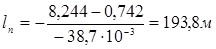 .
.
Таблица 6.4
Результаты вычислений Ux, tx и Рх на участке упругой связи
трубопровода с грунтом
| х, м | b х | Гиперболические функции | Продольные перемеще - ния Ux, мм | Касательные напряжения tх×103, МПа | Продольные усилия Рх, МН | ||
| sh b х | ch b х | ||||||
| 67,3 | 0,52 1,04 1,56 2,08 2,6 3,12 3,5 | 0,544 1,238 2,274 3,937 6,693 11,301 16,5 | 1,138 1,591 2,484 4,062 6,767 11,345 16,5 | 0,050 0,113 0,208 0,360 0,612 1,034 1,510 | -0,40 -0,904 -1,664 -2,88 -4,896 -8,272 -12,08 | 0,045 0,051 0,071 0,112 0,183 0,304 0,510 0,742 | |
Таблица 6.5
Результаты вычислений Uхп и Рхп на участке пластичной связи
трубопровода с грунтом
| х, м | Продольные усилия РХп, МН | Продольные перемещения UХп, мм | х, м | Продольные усилия РХп, МН | Продольные перемещения UХп, мм |
| 0,742 2,29 3,838 | 1,5 7,9 20,9 | 193,8 | 5,386 6,394 8,244 | 40,4 66,5 93,6 |
Определим продольные усилия и перемещения в нескольких сечениях участка lп по формулам (6.84) и (6.85).
При х = 0 UХп определим по формуле (6.77) как при Р0 = Рпр
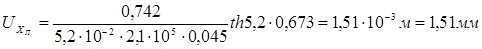
При этом касательные напряжения максимальны и равны предельным: tmax = tпр = -12,08×10-3 МПа. Продольные усилия в том же сечении РХп равны Рпр, т.е. РХп = Рпр = 0,742 МН.
При хп = 40м
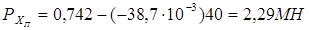 ;
;
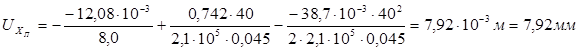 .
.
Результаты вычислений для остальных сечений занесены в табл. 6.5.
Полное перемещение свободного конца участка трубопровода определяем по формуле (6.85)
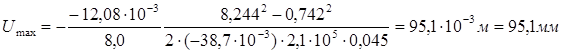 .
.
На рис. 6.12 изображены эпюры распределения продольных перемещений, касательных напряжений и продольных усилий по длине участка трубопровода, рассчитанные в этом примере.
 |
Рис. 6.12. Эпюры распределения Ux, tx и Px по длине
при упругопластической связи
Дата добавления: 2016-04-19; просмотров: 2437;
