Квзілінійна теорія автогенератора

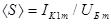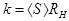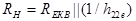Кількісну теорію для розрахунку усталеного режиму автогенератора зручно будувати використовуючи такий параметр як усереднену крутість прохідної характеристики - співвідношення амплітуди першої гармоніки колекторного струму до амплітуди вхідної (базової) напруги. Тоді коефіцієнт підсилення резонансного підсилювача можна визначати як , де - паралельне увімкнення еквівалентного опору навантажувального контуру і вихідної провідності транзистора. При цьому амплітудна умова самозбудження матиме вигляд :

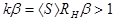(2.1)

У простій лінійній теорії залежність колекторного струму 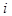від керуючої напруги 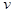апроксимується лінійним законом:

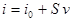(2.2)

(тут і далі ми для спрощення запису формул будемо позначати 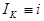та )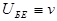

З більшою мірою точності ця залежність може бути апроксимована степеневим багаточленом

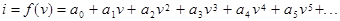(2.3)

що являє собою розклад функції 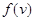у ряд Тейлора в околі робочої точки .

Якщо керуюча напруга являє собою гармонічну функцію

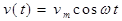(2.4)

то фігуруючі в (2.3) степені 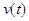матимуть вигляд:

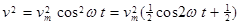
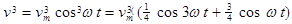
(2.5)

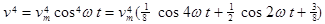
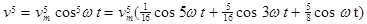
Кожний 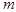-тий член виразу (2.3) буде створювати у струмі 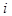вищі гармоніки, аж до 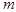-тої. Одначе нас будуть цікавити внески вищих членів ряду (2.3) лише до першої гармоніки колекторного струму 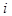, на яку настроєний навантажувальний контур. Амплітуда цієї гармоніки дорівнюватиме

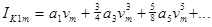(2.6)

Члени парних степенів внесків у амплітуду першої гармоніки не дають.

Поділивши 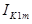на 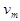, одержимо величину, яка має такий самий зміст, як і 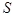при линійній апроксимації (2.2), і яку можна назвати ефективною або середньою крутістю .

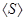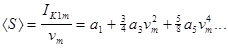(2.7)

Саме її слід підставляти у критерій самозбудження (2.1).

З фізичних міркувань очевидно, що в режимі, який відповідає м’якому самозбудженню, робоча точка лежить на прямолінійній ділянці прохідної характеристики і зі збільшенням амплітуди коливань середня крутість може тільки зменшуватися. Отже. слід очікувати, що у такому режимі 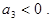Оскільки ж у цьому режимі звичайно 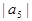<< 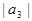, то останнім членом в (2.7) можна поки що знехтувати. Тоді

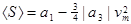(2.8)

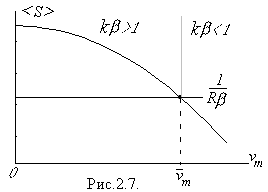
Графік цієї функції зображений на рис.2.7, а умова самозбудження набуває вигляду

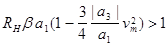(2.9)

Зі зростанням амплітуди коливань член у дужках буде зменшуватися і нерівність перетвориться у рівність, при якій амплітуда коливань не буде ані зростати, ані зменшуватися. Це і є усталений режим Його умова буде

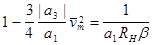(2.10)

а амплітуда усталених коливань 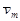буде дорівнюватиме

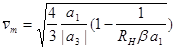(2.11)

Можна довести, що цей режим є стійкий. Дійсно, при зменшенні 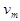середня крутість зростає і критерій самозбудження 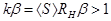стане перевиконаним: коливання зростатимуть і досягнуть попереднього рівня. Якщо ж 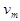збільшиться, то буде 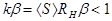, амплітуда коливань зменшуватиметься і знову ж таки повернеться до усталеного рівня.

В режимі жорсткого самозбудження зі зростанням амплітуди коливань середня крутість спочатку зростає, а потім вже зменшується. Отже. можна вважати, що у такому режимі 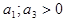, тоді як 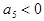і

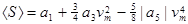(2.12)

Умова усталеної амплітуди матиме вигляд:

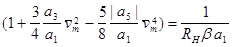(2.13)

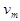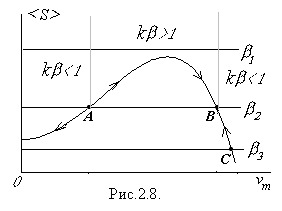
Вираз (2.13) являє собою по відношенню до біквадратне рівняння. У залежності від величини 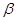воно може мати три типи розв’язків (рис.2.8):

а) для малих 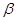(напр. 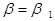) - всі корені комплексні. Дійсних розв’язків немає і самозбудження неможливе;

б) для середніх 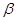(напр. 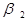) - розв’язком є два дійсних корені [2]. На рис.2.8 це відповідає двом точкам: А (стійка точка) і В (нестійка точка). Коливання можуть підтримуватися, але самозбуджуватися від малого рівня не можуть;

в) Для великих 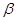(напр. 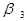) - один корінь уявний, а другий корінь дійсний. Можливе самозбудження коливань з усталеною амплітудою, що відповідає точці С.

Викладена теорія оперує з поняттями, запозиченими з лінійної теорії автогенератора: критерієм самозбудження (1.7) та крутістю. Але крутість тепер вважається не фіксованою і незмінною величиною, а такою, що залежить від амплітуди коливань і цим враховується нелінійність характеристик транзистора. Подібна теорія має назву квазілінійної (тобто неначе лінійної). Вона дозволяє зробити начебто неможливе - розрахувати усталену амплітуду на основі і у термінах лінійної теорії.

Але квазілінійна теорія неспроможна дати відомості про часовий хід процесу усталення коливань - на це здатна лише послідовна нелінійна теорія, яка викладатиметься у курсі “Коливання і хвилі”.

Контрольні питання до розділу