Задания для самостоятельной работы студента. 1. Изучить материалы обязательной и рекомендуемой литературы, данного раздела учебного пособия.
1. Изучить материалы обязательной и рекомендуемой литературы, данного раздела учебного пособия.
2. Изучить технологию выполнения учебного задания на примере задачи-эталона.
3. Ответить на контрольные вопросы и тестовые задания в данном учебном пособии.
4. Решить ситуационные задачи.
5. Применять полученные навыки при выполнении индивидуальных заданий или научно-исследовательской работы.
Блок информации
| 1.Определение | Динамический ряд– ряд однородных величин, характеризующих изменения явления во времени. |
| 2.Область применения | · для характеристики изменений состояния здоровья населения в целом или отдельных его групп, а также деятельности учреждений здравоохранения и изменения их во времени. · для установления тенденций и закономерностей изменений явлений, углубленного анализа динамического процесса (скоростей, временных характеристик текущего и стратегического планирования · для прогнозирования уровней явлений общественного здоровья и здравоохранения |
| 3.Числа (уровни) динамического ряда | Динамические ряды могут быть представлены только однородными величинами: абсолютными, относительными или средними величинами. |
| 4.Типы динамических рядов | Моментный ряд– характеризует изменение значений явления на определенную дату (момент). Интервальный ряд – характеризует изменения значений явления за определенный период (интервал времени). Применяется в случае необходимости анализа процесса в различные дробные периоды. |
| 5.Приемы для установления тенденций или закономерностей | Преобразование ряда – применяется для большей наглядности изменений изучаемых явлений (см. тему «Относительные величины», показатель наглядности). Одно число ряда принимается за 1, чаще всего за 100 или 1000, и, по отношению к данному числу ряда, рассчитываются остальные. Выравнивание ряда – применяется при скачкообразных изменениях (колебаниях) уровней ряда. Цель выравнивания – устранить влияние случайных факторов и выявить тенденцию изменений значений явлений (или признаков), а в дальнейшем установить закономерности этих изменений. |
| 6.Способы выравнивания динамического ряда | Способами выравнивания динамического ряда являются: укрупнение периодов, расчет групповой средней, расчет скользящей средней, метод наименьших квадратов. |
1. Укрупнение периодов – применяется, когда явление в интервальном ряду выражено в абсолютных величинах, уровни которых суммируются по более крупным периодам. Применение возможно при кратном числе периодов
2. Вычисление групповой средней – применяется, когда уровни интервального ряда выражены в абсолютных, средних или относительных величинах, которые суммируются, а затем делятся на число слагаемых. Способ применяется при кратном числе периодов.
3.Расчет скользящей средней – применяется, когда уровни явлений любого ряда выражены в абсолютных, средних или относительных величинах. Данный метод применяется при наличии некратного числа временных периодов (7, 11, 13, 17, 19) достаточно длинного динамического ряда. Путем вычисления групповой средней значений 3 периодов, а в последующем переходя на определенный уровень и два соседних с ним, осуществляется "скольжение" по периодам. Каждый уровень заменяется на среднюю величину (из данного уровня и двух соседних с ним). Данный метод применяется, когда не требуется особой точности, когда имеется достаточно длинный ряд и можно пренебречь потерей двух значений ряда; в случаях, когда изучается развитие явления под влиянием одного или двух факторов.
4. Метод наименьших квадратовприменяется для более точной количественной оценки динамики изучаемого явления. Этим способом получаются такие выровненные значения уровней ряда, квадраты отклонений которых от истинных (эмпирических) показателей дают наименьшую сумму.
Наиболее простой и часто встречающейся в практике является линейная зависимость, описываемая уравнением:
Ух = а + вХ, либоУтеоретич. = Усреднее + вХ,где
Ух – теоретические (расчетные) уровни ряда за каждый период;
а – среднеарифметический показатель уровня ряда, рассчитывается по формуле
а = S Уфакт. /n;
в – параметр прямой, коэффициент, показывающий различие между теоретическими уровнями ряда за смежные периоды, определяется путем расчета по формуле:
в = S (Х Уфакт.) / S Х 2, где
n – число уровней динамического ряда;
Х – временные точки, натуральные числа, проставляемые от середины (центра) ряда в оба конца.
При наличии нечетногоряда уровень, занимающий срединное положение, принимается за 0. Например, при 9-ти уровнях ряда: -4, -3, -2, -1, 0, +1, +2, +3, +4.
При четном числе уровней ряда две величины, занимающие срединное положение, обозначаются через –1 и +1, а все остальные – через 2 интервала. Например, при 6-ти уровнях ряда: -5, -3, -1, +1, +3, +5.
Расчеты проводят в следующей последовательности:
1. Представляют фактические уровни динамического ряда (Уф) (см. табл.).
2. Суммируют фактические уровни ряда и получают сумму Уфакт.
3. Находят условные (теоретические) временные точки ряда Х, чтобы их сумма (S Х ) была равна 0.
4. Возводят теоретические временные точки в квадрат и суммируют их, получая SХ 2.
5. Рассчитывают произведение Х на У и суммируют, получая S ХУ.
6. Рассчитывают параметры прямой:
а = S Уфакт /n в = S (Х Уфакт) / S Х 2
7. Подставляя последовательно в уравнение Ух = а + вХ значения Х, находят выровненные уровни УХ.
Для углубленного изучения процессов во времени рассчитывают показатели динамического ряда.
1. Для характеристики скорости изменения процесса применяются такие показатели, как абсолютный прирост (убыль), темп прироста (убыли).
§ Абсолютный прирост (убыль) характеризует скорость изменения процесса (абсолютную величину прироста (убыли) в единицу времени).Абсолютный прирост рассчитывается как разность между данным уровнем и предыдущим; обозначается знаком «+», характеризуя прирост, или знаком «-», характеризуя убыль.
§ Темп прироста (убыли) характеризует величину прироста (убыли) в относительных показателях в % и определяется как процентное отношение абсолютного прироста (убыли) к предыдущему уровню ряда; обозначается знаком «+» (прирост) или знаком «-» (убыль).
2. Для характеристики изменения процесса одного периода по отношению к предыдущему периоду применяется такой показатель, как темп роста (снижения); рассчитывается как процентное отношение последующего (уровня) к предыдущему.
3. При сравнении динамических рядов с разными исходными уровнями (например, средними, интенсивными, абсолютными) используется показатель – значение 1% прироста (убыли); рассчитывается как отношение абсолютного прироста к темпу прироста за каждый период.
4. Для обобщенной количественной оценки тенденций динамического ряда используется показатель, именуемый средним темпом прироста (снижения)
“Т пр.сн.”, выраженный в %. При его расчете для большинства рядов можно использовать следующую формулу:
Т пр.сн = 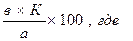
К = 1 при нечетном числе уровней ряда;
К = 2 при четном числе уровней ряда;
а и в – показатели линейной зависимости, используемые при выравнивании ряда методом наименьших квадратов.
Задача-эталон
Условие задачи: В Н-ском районе изучена заболеваемость населения ветряной оспой за 10 лет (см. таблица 4.8.1).
Таблица 4.8.1
Дата добавления: 2016-02-16; просмотров: 1560;
