Общий физический закон сохранения энергии, законы сохранения и симметрия в пространстве и времени.

Яворский «Курс физики» стр. 60 прагр.5-6.

Сумму 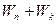тел называют полной механической энергией.

Полная механическая энергия замкнутой системы тел остается неизменной при любых движениях тел этой системы, если между телами действуют силы тяготения или упругости.

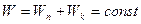
Глава 4.

Принцип относительности в механике.

Элементы релятивистской динамики.

Инерциальные системы отсчета и принцип относительности Галлилея. Инварианты преобразований Галилея.

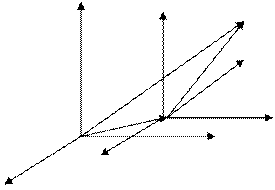Рассмотрим две инерциальные системы отсчета (ИСО), движущиеся относительно друг друга с некоторой постоянной скоростью 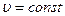. Условно примем за неподвижную систему отсчета XYZ, а за подвижную - X`Y`Z`.

Z Z`

M

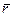
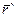
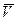
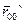o` Y`

Y

o X`

X

Из чертежа видно, что между радиус-векторами 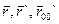существует связь:

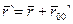(4.1)

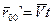(4.2)

При этом мы предположим, что в начальный момент времени точки О и О` совпадают:

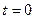
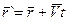(4.3)

Кроме соотношения (4.3) необходимо установить связь между значениями времени в системе отсчета XYZ и временем в X`Y`Z`

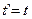(4.4)

предположим, что это время течет одинаково.

Соотношения (4.3) и (4.4) выражают преобразования Галилея.

Запишем эти преобразования в скалярной форме:

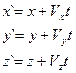(4.5)

Наиболее просто преобразования Галилея выглядят в том случае, когда 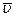направлен вдоль одной из осей координат.

Предположим, что 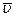направлен вдоль оси Х, тогда:

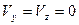
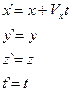следовательно: (4.6)

Если соотношение (4.3) продифференцировать по времени, то получим:

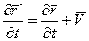(4.7)

Ясно, что: 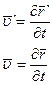(4.8)

Тогда (4.7) приобретает вид:

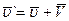(4.9)

формула (4.9) выражает собой теорему сложения скоростей в классической механике.

Теорема: Скорость движения · относительно системы К равна сумме скорости движения · относительно системы К и скорости системы К` относительно системы К.

Рассмотрим, как меняется расстояние между двумя ·ми при переходе от одной СО к другой.

Пусть имеются две ·ки М₁ и М₂, их радиус-векторы r₁ и r₂, и, соответственно 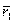и 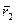в другой СО.

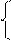Тогда: 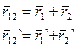(4.10)

Если в (4.10) подставить (4.3), то мы увидим, что:

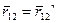(4.11)

Т. е. расстояние между двумя · не меняется, такие величины называют инвариантами соответствующих преобразований координат.

Аналогично можно показать, что не меняется и скорость относительного движения двух ·.

Дифференцируя по времени (4.10) получаем:

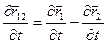
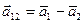
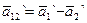
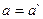
Силы взаимодействия между двумя · могут зависеть либо от расстояния между ними, либо от скорости их относительного движения, или и от одного и от другого.

Т. к. обе эти величины инвариантны относительно преобразований Галилея следовательно инвариантом является и сила.

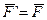(4.12)

Рассмотрим второй и третий законы Ньютона.

В разных СО эти законы имеют разный вид:

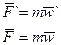(4.13)

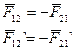(4.14)

Инвариантность третьего закона Ньютона вытекает из соотношения (4.12).

Что касается второго закона Ньютона, то необходимо установить связь между ускорениям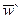и и .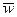

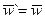(4.15)

Таким образом, ускорение также инвариант, и, следовательно, второй закон Ньютона инвариантен относительно преобразований Галилея.

Итак, можно сделать вывод:

Все законы механики одинаковы в любых инерциальных системах отсчета. Это утверждение называют ПРИНЦИПОМ ОТНОСИТЕЛЬНОСТИ ГАЛЛИЛЕЯ.

Существует еще одна формулировка принципа Галлилея:

Никакими механическими опытами, поставленными в ИСО, невозможно установить движется эта система или покоится.

Следствием из принципа Галилея является тот факт, что все ИСО эквивалентны, равносильны.