Минимизация логической функции с помощью карты Карно
Минимизация логической функции с помощью карты Карно осуществляется по следующему алгоритму:
· Для получения ДНФ все единицы объединяются в прямоугольные контуры, не содержащие внутри нулей, с числом клеток в контуре 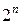 , где n = 0, 1, 2, 3,...
, где n = 0, 1, 2, 3,...
· Контур проводится через соседние клетки, т.е. клетки, отличающие значением только одной переменной.
· Контуры могут частично накладываться друг на друга и должны иметь максимальные возможные размеры.
· Единичному контуру соответствует произведение переменных, в области единичного значения которых он находится полностью, т.е. границ их изменения не пересекает.
· ДНФ получается в виде суммы значений всех единичных контуров.
· Для получения минимальной ДНФ размеры контуров должны быть максимальны, а их число минимально.
· Для получения КНФ все нули объединяются в прямоугольные контуры, не содержащие внутри единиц, с числом клеток в контуре 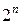 , где n = 0, 1, 2, 3...
, где n = 0, 1, 2, 3...
· Контур проводится через соседние клетки, т.е. клетки, отличающие значением только одной переменной.
· Контуры могут частично накладываться друг на друга и должны иметь максимальные возможные размеры.
· Нулевому контуру соответствует сумма инвертированных значений переменных, в области единичного или нулевого значения которых он находится полностью, т.е. границ их изменения не пересекает.
· КНФ получается в виде произведения значений всех нулевых контуров.
· Для получения минимальной КНФ размеры контуров должны быть максимальны, а их число минимально.
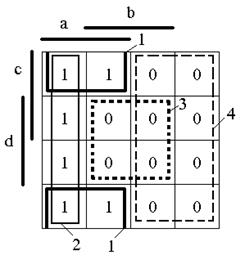
Пример: Минимизировать карту Карно, приведенную на рис.4.2.
|
Рис.5.2 Карта Карно с единичными и нулевыми контурами
Анализ единичных контуров дает следующее выражение для ДНФ
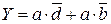 (5.3)
(5.3)
/ \
контур 1 контур 2
Анализ нулевых контуров дает следующее выражение для КНФ
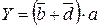 (5.4)
(5.4)
/ \
контур 3 контур 4
Дата добавления: 2016-04-14; просмотров: 987;
