Моделирование турбин и принципы подобия

1. Общие положения

К гидротурбине, как и ко всякой другой машине, предъявляются следующие основные требования.

1. Обеспечение высокой надёжности при длительной её эксплуатации.

2. Обеспечение высоких энергетических и кавитационных показателей турбины при всевозможных режимах её работы, характеризуемых значениями КПД и кавитационных коэффициентов.

3. Получение требуемой мощности при данном рабочем напоре при минимальных размерах и массе турбины и вспомогательного оборудования.

4.Конструкция и компоновка гидротурбинного оборудования при заданной его принципиальной конструкции должны удовлетворять требованиям удобного размещения этого оборудования в зданиях ГЭС минимальных размеров.

Эти задачи в современных условиях решаются путём проведения гидромеханических и прочностных расчётов деталей и узлов гидротурбинного оборудования, а также путём постановки энергетических, кавитационных и прочностных испытаний моделей в лабораторных условиях. При проектировании новых гидротурбин используются также опытные данные, полученные при испытаниях и эксплуатации аналогичных по конструкции турбин на действующих ГЭС.

Исследования рабочих процессов на моделях и распространение их результатов на натурные турбины основаны на теории подобия гидромеханических процессов в потоке жидкости.

В основе моделирования лежат три условия.

1. Условие геометрического подобия.

Это условие сводится к подобию конфигураций обтекаемых поверхностей элементов проточной части турбины, т.е. требуется, чтобы все сходные линейные размеры обтекаемых поверхностей турбины были пропорциональны и расположены под одинаковыми углами.

Для соблюдения геометрического подобия моделируются обтекаемые поверхности следующих частей турбины: спиральной камеры, направляющего аппарата (по форме его лопаток и величине открытия), рабочего колеса и его камеры и отсасывающей трубы.

Иногда производят моделирование только рабочего колеса, а влияние не моделируемых при этом частей учитывают путём внесения соответствующих поправок в характеристику, получаемую при испытаниях.

Турбины разных размеров, но с геометрически подобной конфигурацией обтекаемых поверхностей и их проточной части, образуют турбинную серию.

2. Условие кинематического подобия.

Оно заключается в том, что во всех сходных точках потока скорости течения пропорциональны между собой, а направление одноимённых скоростей – одно и то же. Условие сводится к подобию картины течения потоков жидкости внутри проточной части сравниваемых турбин. При этом очевидно, что абсолютная, окружная и относительная скорости соответственно в сходных точках потока геометрически подобных турбин имеют одинаковое направление и пропорциональны по величине. Иначе говоря, условие кинематического подобия сводится к подобию треугольников скоростей в соответствующих точках потока. Режимы работы турбин, характеризуемые кинематическим подобием, называют изогональными.

3. Условие динамического подобия.

Динамическое подобие предполагает равенство отношений одноимённых сил, отнесённых к единице объёма и действующих на сходные элементы модели и турбины.

1. Турбины одного типа и закон подобия режимов их работы

Тип турбины определяется формой («геометрией») её проточного тракта. Иными словами, все турбины данного типа имеют геометрически подобную проточную часть. Следует подчеркнуть, что размер турбины не участвует в определении её типа.

В соответствии с принятым определением две турбины одного типа, но различного размера удовлетворяют следующим условиям:

1) все соответственные углы в них равны:

δ₁₁ = δ₁₂; δ₂₁ = δ₂₂; δ_i1 = δ₁₂; (1)

2) отношение всех соответствующих углов постоянно:

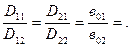… (2)

Режимы турбин одного типа будут подобны, если сохраняется геометрическое подобие параллелограммов или треугольников скоростей в соответствующих точках проточного тракта.

Следовательно, при подобии режимов:

1) направления всех соответствующих скоростей должны быть одинаковыми, т.е. все соответственные углы равны:

α_i1 = α_i2 ; β_i1 = β_i2 (3)

как отмечалось выше, такие режимы будут изогональными;

2) отношения всех скоростей в соответствующих точках должны иметь постоянное значение:

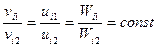(4)

установим теперь на основании приведённых определений закономерности, определяющие соотношения между параметрами турбин одного типа в условиях подобия режимов их работы.

Задача.

Имеем две турбины одного типа, но различного размера D₁ и D₂, напоры Н₁ и Н₂. Углы установки лопаток направляющего аппарата и лопастей рабочего колеса равны: . α₀₁ = α₀₂ и φ₁ = φ₂

Каковы должны быть соотношения частот вращения n₁ и n₂, расходов Q₁ и Q₂ и мощностей N₁ и N₂, чтобы режимы работы обеих турбин были подобны?

Решение.

Прежде всего используем геометрические (1), (2) и кинематические (3), (4) соотношения.

Так как 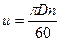, то

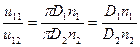(5)

Так как

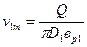, то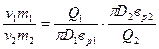

Учитывая, что 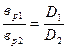получаем

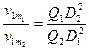(6)

Поскольку по (4) при сохранении режимов 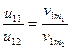, приходим к равенству

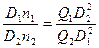или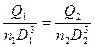

Обобщая этот результат, записываем кинематическое условие подобия (сохранения) режима работы турбины:

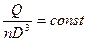(7)

Теперь используем энергетические соотношения, учитывая, что эти турбины работают при разных напорах Н₁ и Н₂ и имеют гидравлические КПД η_Г1 и η_Г2.

Напишем уравнение Эйлера для каждой из турбин:

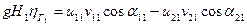(8)

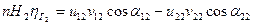(8а)

из условий подобия (3) и (4) и из формулы (5) следует, что

α₁₁ = α₁₂; α₂₁ = α₂₂ 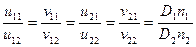и или

cos α₁₁ = cos α₁₂ cos α₂₁ = cos α₂₂

Следовательно,

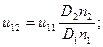
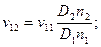
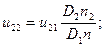
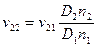
Подставим полученные соотношения в правую часть (8 а):

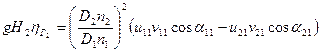
(8 б)

Разделив (8) на (8 б), получаем выражение

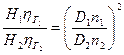
Отсюда находится соотношение между частотами вращения:

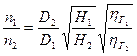(9)

Подставив найденное отношение 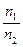в кинематическое условие подобие (7)

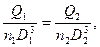
получим соотношение расходов

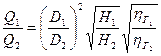. (10)

Соотношения мощностей легко получить из формул N₁ = 9,81 Q₁H₁η₁ и N₂ = 9,81Q₂H₂η₂,

используя (10):

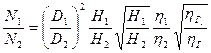(10 а)

Формулы (9), (10), а также (10 а) называются Законами (формулами) подобия и очень широко используются. Поскольку гидравлический КПД изменяется мало, то часто для упрощения считают .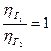

1. Приведённые параметры турбин

Турбины могут выполняться самых различных размеров и работать в широком диапазоне напоров, частот вращения, расходов и мощности. Следовательно, для характеристики турбины данного типа нужны какие-то показатели, приведённые к общим, стандартным условиям, например, по напору и диаметру. Принято давать показатели турбины, пересчитанные на напор Н = 1 м и диаметр D = 1 м. Эти параметры называются приведёнными (единичными) и обозначаются 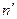– приведённая частота вращения и 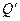- приведённый расход. Используя формулы пересчёта (9) и (10) без учёта изменения КПД по заданным параметрам турбины n₁, Н и D, получаем: 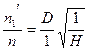или

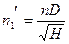(11)

Также из формул пересчёта можно получить

,

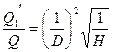откуда 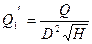(12)

Значения приведённых параметров 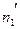и 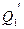в подобных режимах практически сохраняются неизменными, причём их определяют по результатам модельных испытаний. По известным значениям приведённых параметров с помощью (11) и (12) легко определить частоту вращения n и расход Q натурной турбины данного типа по заданным напору и диаметру:

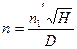(13)

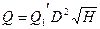
(14)

Приведённые (единичные) параметры широко используются для характеристик турбин.

1. Коэффициент быстроходности

Для суммарной характеристики гидравлических качеств турбин по скорости вращения и по пропускной способности, а также для сравнения между собой различных систем турбин и типов рабочих колёс в практике гидромашиностроения используют так называемый коэффициент быстроходности n_s.

Коэффициент быстроходности n_s численно равен частоте вращения турбины данного типа, но такого размера, что при напоре Н = 1 м она развивает мощность 1 л.с. (1 л.с. = 0,736 кВт).

Найдём коэффициент быстроходности турбины, если известны её частота вращения n, напор Н и мощность D.

На основании (9)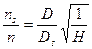

Здесь D_S – диаметр турбины, мощность которой равна 1 л.с.

По (10 а) без учёта изменения КПД

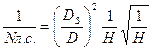
Возведём первое уравнение в квадрат

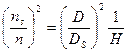
и перемножим второе и третье уравнения. Это позволит исключить D_S.

Тогда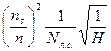

Отсюда получаем формулу для определения коэффициента быстроходности:

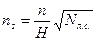(15)

Можно найти связь между коэффициентом быстроходности n_s и приведёнными единичными параметрами турбины 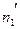и .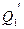

Выразив расход через Q₁^' (по 14), без учёта изменения КПД получим:

,

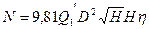подставив в (15) мощность N в л.с. и n по (13), имеем:

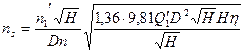
откуда окончательно

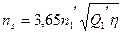(16)

Уравнение (16) показывает, что в изогональных режимах коэффициент быстроходности турбин одной и той же серии с точностью до КПД равны между собой, так как при этих условиях 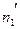и 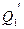остаются постоянными. С переменой режима работы турбины, т.е. с изменением мощности или числа оборотов при данном напоре, коэффициент быстроходности также меняет свою величину. Поэтому сравнивание между собой турбин различных серий по коэффициентам можно производить только при условии вычисления их для одинаковых режимов сравниваемых турбин.

Коэффициент быстроходности обычно определяется для режима максимальной мощности. Он весьма полно характеризует свойства турбины, форму рабочего колеса, т.е. её вид и тип. Коэффициенты быстроходности n_s различных видов турбин изменяются следующим образом:

Турбины: n_s

осевые поворотно-лопастные 1200 – 450

радиально-осевые 400 - 80

ковшовые 50 - 10

Чем меньше коэффициент быстроходности n_s, тем тихоходнее турбина, тем выше и её область напоров.

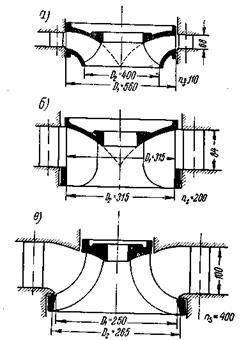
Для наглядности на рис. 19 показаны три типа рабочих колёс радиально-осевых гидротурбин, каждое из которых развивает мощность в 1 л.с..

У тихоходного колеса (рис. 19, а) входной диаметр D₁ больше выходного диаметра D₂; у быстроходного же колеса (рис. 19, в) входной диаметр D₁ меньше выходного диаметра D₂.

Рис. 19 Рабочие колеса различной быстроходности: а-тихоходные; б- средней быстроходности; в- быстроходные.

Другая характерная особенность этих колёс заключается в том, что с повышением коэффициента быстроходности n_s увеличивается отношение высоты лопаток направляющего аппарата к входному диаметру D₁.

1. Выводы

Получить наивысший КПД только на основе теоретических расчётов, как правило, не удаётся. Требуется экспериментальная доработка всех элементов проточной части турбины, которая производится на моделях в лабораториях.

Для этих целей должны быть соблюдены три условия подобия:

1. Условие геометрического подобия.

2. Условие кинематического подобия.

3. Условие динамического подобия.