Режим работы турбины

Рассмотренный способ построения параллелограммов (треугольников) скоростей показывает, что для данного рабочего процесса при неизменном открытии направляющего аппарата (α₀ = const) форма параллелограммов скоростей, определяемая углами α и β, зависит от частоты вращения n и расхода Q.

Рассмотрим, как эти параметры влияют на течение.

Пусть расход Q сохраняется, а изменяется частота вращения n. При этом на входных кромках I лопастей рабочего колеса 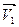будет сохранять неизменное значение, так как, согласно (10), 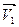не зависит от n. Изменяться будут только 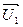и .

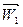V₁ = V_1m + V_1u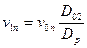

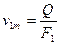
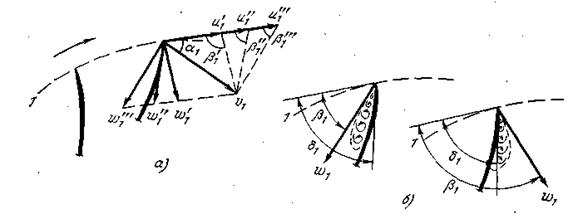
Рис. 15. Течение на входных кромках рабочего колеса

Из построения видно, что вектор относительной скорости 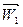меняет своё направление. При малой частоте вращения он отклоняется в сторону вращения, 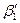> δ₁ , а при большой – в противоположную сторону, 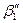< δ₁. Когда β₁ <>δ₁, натекание жидкости на входную кромку лопасти происходит под углом, что сопровождается образованием вихревых зон, создающих дополнительные потери энергии (потери на удар).

Наиболее благоприятным является режим безударного входа, когда β₁ = δ₁.

На выходных кромках 2 относительная скорость 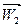, согласно (12)– ( 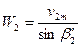), зависит только от расхода Q и угла δ₂, т.е. не зависит от n. Однако, поскольку u₂ пропорционально n, то абсолютная скорость 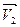будет зависеть и от n. Эту зависимость легко проследить по параллелограммам скоростей на выходных кромках рабочего колеса радиально-осевой и осевой турбины.

При этом можно отметить следующее:

1. Хотя расход постоянен, значение вектора скорости 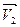зависит от n и минимальное значение его модуля соответствует условию, при котором вектор 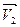лежит в меридианной плоскости (направлен к центру или параллелен оси вращения), т.е., когда α₂ = 90⁰.

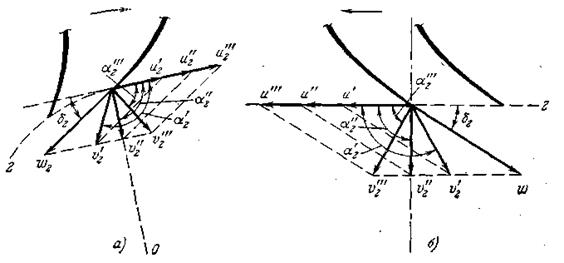
Рис 16. Течения на выходных кромках рабочего колеса.

2. В общем случае поток за рабочим колесом имеет закрученность (циркуляция Г₂ ≠ 0), причём, если α₂ < 90⁰, то направление закрутки потока совпадает с направлением вращения рабочего колеса, если же α₂ > 90⁰, то поток вращается в обратном направлении. Только при α₂ = 90⁰ циркуляция Г₂ = 0.

Режим, соответствующий условию α₂ = 90⁰ , когда значение v₂ минимально, а Г₂ = 0, называют режимом нормального выхода.

Поскольку потери на выходе из рабочего колеса в общем пропорциональны v₂, то режим работы турбины, близкий к режиму нормального выхода, даёт наименьшие потери, т.е. является наиболее благоприятным.

Режим, при котором одновременно удовлетворяются и условия безударного входа и нормального выхода, обеспечивающие минимальные потери, т.е. наивысший КПД турбины, называют оптимальным режимом.

1. Основное энергетическое уравнение турбины

Для определения силовых и энергетических показателей потока в рабочем колесе применим закон момента количества движения в форме (3) - .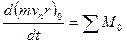

Рассмотрим радиально-осевую турбину (рис. 17) и выделим контрольными поверхностями 1 и 2 область, включающую в себя лопасти рабочего колеса.

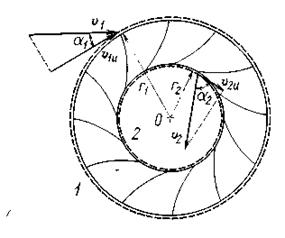
Рис. 17. Скорости на входной и выходной кромках лопастей рабочего колеса.

Для установившегося осреднённого потока внутри выделенной области v_u r не изменяется во времени и, следовательно, d(v_u r) равно разности (v_1u r₁ – v_2u r₂) на контрольных поверхностях. Протекающая через рабочее колесо за время dt масса жидкости равна

m = ρQdt

В этих условиях закон момента количества движения представляется формулой

ρQ(v_2u r₂ – v_1ur₁) = Σ M₀ (14)

Сумма моментов внешних сил относительно оси вращения ΣM₀ , действующих на выделенный объём жидкости, определяется следующим образом. Момент от сил давления на поверхность вращения 1 и 2 и поверхности ободов равен нулю. Силы веса также не дают момента, так как центр их приложения совпадает с осью. Остаются силы трения по ограничивающим поверхностям и силы давления и трения жидкости на лопастях.

Обе группы сил дают момент относительно оси, но первую из-за малости можно не учитывать, и тогда остаётся момент, воздействующий на жидкость со стороны лопастей рабочего колеса М. Искомый же момент рабочего колеса, создаваемый жидкостью на лопастях будет равен этому моменту ( М).

В итоге, по (14), раскрывая значения v_1u и v_2u, получаем:

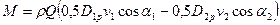(15)

Используя выражения средней циркуляции

Г₁ = πD_1р v₁ cos α₁ и

Г₂ = πD _2р v₂ cos α₂ (16)

можно выразить момент рабочего колеса через разность средних циркуляций на входе и выходе:

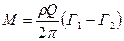(17)

Последняя формула особенно наглядна. Она показывает, что на рабочем колесе создаётся крутящий момент только в том случае, когда оно воздействием своих лопастей изменяет циркуляцию потока.

Знак Г принимается положительным, если V_u совпадает с направлением окружной скорости U.

Зная момент и задавая угловую скорость рабочего колеса, можно определить развиваемую им мощность:

N_р.к. = Mω (18)

Здесь М – в нм, ω – в 1/с, N_р.к – в Вт.

В то же время известно, что мощность турбины выражается формулой:

N = ρgQHη

Это позволяет составить равенство

Mω = ρgQHη_г

где Н – напор турбины,

η_г– гидравлический КПД.

Подставляя в эту формулу М по (15) и учитывая, что ω 0,5D_1р = u₁ и ω 0,5D_2р = u₂ - окружные скорости, получаем

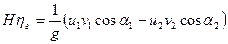(19)

Используя формулу (17), приходим к другой форме выражения:

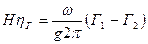(20)

Формулы (19) и (20) представляют собой основное уравнение турбины, или уравнение Эйлера. Левая часть Нη_Г – энергия в Дж, полученная рабочим колесом от жидкости весом в 1Н, прошедшей через лопастную систему рабочего колеса. Правая часть содержит кинематические параметры потока при входе на рабочее колесо и после выхода из него.

Таким образом, основное уравнение даёт связь между энергетическими и кинематическими параметрами в турбине.

Из уравнения Эйлера можно сделать важные выводы:

1. Наиболее благоприятный по КПД режим работы близок к условиям нормального выхода, когда циркуляция Г₂ = 0 или мала. Г₁ = Г₀ – циркуляция равна создаваемой направляющим аппаратом. Отсюда можно определить требуемое значение Г в зависимости от Н и ω.

2. В процессе прохождения воды через рабочее колесо турбины циркуляция потока должна убывать. Следовательно, рабочее колесо «срабатывает» циркуляцию, созданную направляющим аппаратом.

1. Особенности рабочего процесса ковшовых турбин

Отличие активных ковшовых турбин от реактивных состоит в том, что у них рабочее колесо вращается в воздухе и может использовать только кинетическую энергию жидкости, а вода одновременно воздействует только на часть лопастей. Эти два фактора определяют и некоторые особенности рабочего процесса ковшовых турбин.

При всех открытиях иглы направление и значение скорости струи v_с сохраняются постоянными (коэффициент скорости φ изменяется очень мало). Скорость на входной кромке лопасти 1 практически равна скорости струи .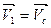

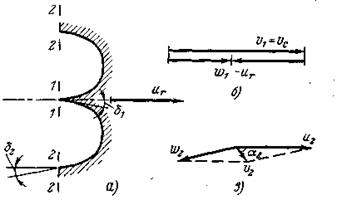
Рис. 18. Кинематика потока в рабочем колесе ковшовой турбины

Окружная скорость (переносная) для данного сечения лопастей, расположенного на расстоянии r от оси вращения, определяется выражением

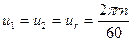(среднее значение r_ср = 0,5D₁)

При этом параллелограмм скоростей 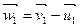на входной кромке лопасти вырождается в прямую линию (рис. 18,б) и w₁ совпадает с направлением струи. Следовательно, для приближения к условиям безударного входа угол входной кромки δ₁ должен быть минимальным («нож»).

Параллелограмм скоростей на выходной кромке определяется тем, что в процессе движения по лопасти относительная скорость изменяется мало и можно принять W₂ =W₁, а её направление совпадает с δ₂. В итоге получаем (рис. 18,в):

.

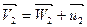Поскольку угол δ₂ мал, параллелограмм получается вытянутым и, несмотря на высокие значения скоростей W₂ и u₂, скорость v₂ оказывается небольшой. Минимальное значение v₂ соответствует α₂ = 90⁰ - условию нормального выхода.

Кинематика течения жидкости показывает, что рабочее колесо ковшовой турбины также изменяет момент скорости жидкости относительно оси вращения и, следовательно, для определения момента рабочего колеса можно использовать зависимость:

.

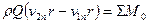В итоге можно получить и уравнение Эйлера в форме (19).

1. Потери энергии и КПД

Подведённая к турбине мощность потока в кВт

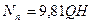
Мощность, развиваемая турбиной, несколько меньше подведённой мощности из-за различных потерь и составляет

,

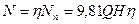где η – полный КПД турбины.

Потери мощности Δ Ν = (1 - η)Ν_п . Они складываются из объёмных, гидравлических, механических и других потерь.

Объёмные потери Δ Q

Эти потери вызваны тем, что не вся вода, подведённая к турбине, проходит через рабочее колесо. Небольшая часть её проходит через зазоры между вращающимся рабочим колесом и сопряжёнными с ним неподвижными частями и в процессе работы не участвует. Если полный расход Q, утечки через щелевые зазоры – ΔQ, то расход через рабочее колесо

Q_к = Q – ΔQ = η_q Q

где 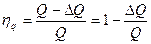- объёмный КПД (21)

Гидравлические потери

К числу гидравлических относятся потери:

1. на удар при входе на рабочее колесо;

2. на гидравлическое сопротивление по длине водопроводящего тракта в пределах турбины (путевые потери);

3. на изменение скорости по величине и направлению (местные потери);

4. значительная часть скоростных потерь на выходе из отсасывающей трубы.

Все гидравлические потери учитываются КПД (η_Г)

Н_Г = Н – Δ Н = η_гН

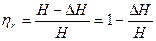(22)

Кроме того, гидравлический КПД можно рассматривать как отношение гидравлической мощности Ν_Г , передаваемое рабочему колесу турбины, к мощности 9,81 η_ηQН, которой обладает поток воды с расходом η_ηQ.

Гидравлическая мощность в кВт

Ν_Г = 9,81 η_Г η_η QН (23)

Суммарные гидравлические потери в кВт

Δ Ν_Г = 9,81(1 - η_Г) η_η QН (24)

Механические и другие потери

Не вся мощность, развиваемая рабочим колесом турбины, передаётся генераторному валу, так как некоторая её доля ΔΝ идёт на преодоление трения во вращающихся частях турбины: в подшипниках, подпятниках, лабиринтах; на дисковое трение, вентиляцию; на привод механизмов, связанных с валом турбины и предназначенных для её обслуживания и др. Эти потери учитываются механическим КПД η_м , представляющим отношение полезной мощности Ν к гидравлической мощности турбины Ν_Г. Поэтому

Ν = η_м Ν_Г = 9,81η_м η_Г η_q QН (25)

Следовательно, полный КПД турбины

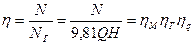(26)

Механические потери

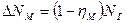(27)

Главные потери энергии

Для различных систем и типов гидротурбин по-разному распределяются отдельные составляющие потерь мощности и энергии. Так же по-разному распределяются потери при различных режимах работы турбины, характеризуемые величиной мощности при данном рабочем напоре. Именно поэтому нельзя указать точные значения тех или иных потерь и их удельное значение в общем балансе энергии. однако имеется возможность указать на те потери энергии, которые в значительной мере влияют на величину общего значения КПД.

Для быстроходных турбин

(пропеллерные, поворотно-лопастные, радиально-осевые),

главными потерями будут гидравлические, т.к. эти турбины обычно работают при низких напорах и больших расходах.

Для тихоходных радиально – осевых турбин

значительными потерями будут объёмные и механические на дисковое трение, т.к. эти турбины работают при высоких напорах с малыми расходами воды. При малых расходах Q всякая утечка воды через зазоры турбины оказывает заметное влияние на величину потерь, а поэтому и на величину объёмного КПД.

У ковшовых турбин значительные потери энергии имеют место в подводящем сопле. Величина их

Δ Н = (1 - φ² )Н

При φ = 0,97 эти потери будут составлять около 6 %.

Выводы

Основное уравнение турбины определяет связь между энергетическими и кинетическими параметрами в турбине и даёт возможность определить наиболее оптимальный режим работы турбины.