Поток, создаваемый направляющим аппаратом реактивных турбин
Во всех реактивных турбинах поток, поступающий на рабочее колесо, формируется направляющим аппаратом, представляющим собой круговую решётку профилей (лопаток).
Характерными показателями круговой решётки являются форма профилей и густота решётки. Профиль лопатки бывает симметричным, когда средняя линия профиля прямая и несимметричным, когда средняя линия искривлена.

 Симметричный профиль. Несимметричный профиль.
Симметричный профиль. Несимметричный профиль.
Рассмотрим поток, создаваемый направляющим аппаратом (см. рис. 9).
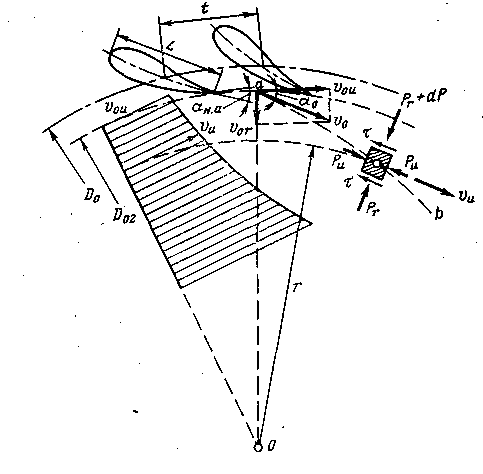
Рис. 9 Поток, создаваемый направляющим аппаратом
Как видно из рисунка, расстояние между смежными профилями по средним линиям t – шаг решётки, а длина хорды L – длина профиля. Отношение L / t – показатель густоты решётки.
Поскольку лопатки направляющего аппарата должны обеспечивать полное закрытие турбины, то всегда L / t > 1, обычно около 1,1.
Таким образом, направляющий аппарат представляет собой достаточно «густую» решётку, у которой при выходе на диаметре D0 2 направление скоростей жидкости voблизко к направлению выходных кромок лопаток: α = αн.а.
Для радиального направляющего аппарата, применяющегося в большинстве реактивных турбин, вектор vo можно представить суммой двух слагаемых:
vo=vor + vou ,
в которой vor - радиальная компонента;
vou - окружная компонента.
Зная расход турбины Q и размеры направляющего аппарата, радиальную компоненту определяем по формуле:
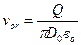 (1)
(1)
где D0 – средний диаметр;
во - высота направляющего аппарата.
Угол между voи vou обозначим α0, тогда
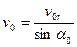 , (1 а)
, (1 а)
а окружную составляющую определяем из соотношения
v0 u = v0 cos α0 (1 б)
Наличие окружной компоненты v0 u указывает на то, что поток за направляющим аппаратом «закручен» относительно оси 0.
«Закрученность» потока определяется так называемой циркуляцией Г, которая в общем случае выражается формулой
 Г = ∫s vcos(v^dS)dS (2)
Г = ∫s vcos(v^dS)dS (2)
здесь S – замкнутый контур, проведённый внутри потока и v^dS - угол α между двумя направлениями v и dS(см. рис. 10)

Рис. 10 К определению циркуляции потока
Из формулы видно, что циркуляция Г измеряется в м2/с.
Для осреднённого потока за направляющим аппаратом на выходном диаметре D0 2 циркуляция равна
Г = πD02 v0 cos α0 (2 а)
Отсюда следует, что направляющий аппарат создаёт циркуляцию потока Г0 .
В пространстве между концами направляющих лопаток и входными кромками лопастей рабочего колеса (иногда его называют «предколёсное пространство») жидкость движется свободно, а траекторией частиц является кривая ав. Важно установить, как при этом изменяется скорость.
Выделим из этой траектории элементарную массу m на радиусе r. Используем известный закон механики о моменте количества движения: для выделенной массы производная по времени от момента количества движения относительно некоторой оси равна сумме моментов всех внешних сил, действующих на эту массу относительно той же оси. Этот закон представляется формулой:
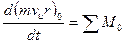 (3)
(3)
где:
m – масса жидкости выделенного объёма;
vu – окружная компонента скорости;
r - радиус;
Σ М0 – сумма моментов внешних сил, действующих на выделенную массу, относительно оси 0 .
Рассмотрим внешние силы. Давления, имеющие радиальные направления Рr и Рr + dР момента относительно центра 0 не образуют. Давления на торцевые поверхности Р п в условиях осреднённого потока равны и также не дают момента относительно оси 0. Остаются касательные усилия τ от трения жидкости, но из-за малости их можно не учитывать.
В итоге получаем, что при свободном движении жидкости можно принять Σ М0 = 0, а это значит, что
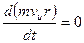 или mvu r = const
или mvu r = const
Отсюда вытекает чрезвычайно важная зависимость
vu r = const (4)
определяющая условия свободного движения жидкости и называемая законом постоянства момента скорости.
Зависимость (4) показывает, что по мере приближения к оси 0 окружная составляющая скорости возрастает и на радиусе r
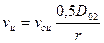 ,
,
т.е. эпюра vu (r) представляет собой гиперболу. С учётом того, что Г = 2 πrvu из (4) вытекает условие постоянства циркуляции при свободном движении жидкости.
Г = Г0 = const (4 а)
Следовательно, в пространстве между направляющим аппаратом и рабочим колесом турбины циркуляция, созданная направляющим аппаратом турбины, сохраняется.
- Кинематика потока в рабочем колесе реактивных турбин
Преобразование энергии жидкости в механическую энергию на валу осуществляется в рабочем колесе за счёт взаимодействия потока с лопатками рабочего колеса, представляющего собой решётку профилей.
При исследовании потока жидкости в рабочем колесе это движение рассматривается как сложное, состоящее из двух движений: относительного и переносного. Относительное движение жидкости фиксируется «наблюдателем», находящимся на рабочем колесе (картина относительного движения может быть получена на фотографии, если её снять фотоаппаратом, вращающимся вместе с рабочим колесом). Переносное движение определяет движение самого рабочего колеса и его лопастей. В турбинах это всегда – вращение. Сумму относительного и переносного движений называют абсолютным движением.
Если обозначить вектор скорости относительного движения Wи скорости переносного движенияU, то вектор абсолютной скорости V определяется векторной суммой
V = U + W
Отсюда следует, что соотношения междуV,U и W устанавливаются параллелограммом или треугольником скоростей.
Рассмотрение конструкций турбин показывает, что формы рабочих колёс разных видов турбины, а у одного вида – для различных напоров, существенно изменяются. Поэтому необходимо установить некоторые принципы определения геометрических характеристик различных рабочих колёс, позволяющих осуществить построение параллелограмма скоростей.
Рассмотрим наиболее общий случай: рабочее колесо радиально-осевой турбины, на меридианное сечение снесены все точки входной кромки лопастей, обозначенные индексом I, и точки выходной кромки, обозначенные индексом 2 (рис. 11).
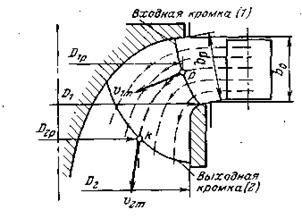
Рис. 11 Меридианный поток в радиально-осевой турбине.
Поток, выходящий из направляющего аппарата, разделён на несколько равных по площади и высоте слоёв и траекторию каждого слоя в колесе также снесём на меридианную плоскость.
Получим кривые линии (пунктирные), причём поверхности вращения каждой такой линии представляют собой поверхности тока, т.е. поверхности, которые не пересекаются движущейся жидкостью (движение представляется слоистым).
Таким образом, кривые линии на меридианной плоскости являются сечениями поверхностей тока.
Очевидно, чтобы установить полную картину потока в рабочем колесе, нужно рассмотреть течение по всем меридианным поверхностям тока. Но, с целью упрощения, можно выделить одну, наиболее характерную кривую, например среднюю рk, и по ней проанализировать условия течения.
Представим себе сечение лопастей рабочего колеса средней поверхностью тока (кривая pk). Это будут некоторые пространственные формы. Для удобства построений эти сечения сносятся на плоскость, причем сохраняются фактические значения углов (если линия pk близка к прямой, то это можно осуществить путем развертки конического или цилиндрического сечения, если криволинейная, то отоброжением).
Рассмотрим сечение рабочего колеса радиально-осевой турбины (рис. 12,а).
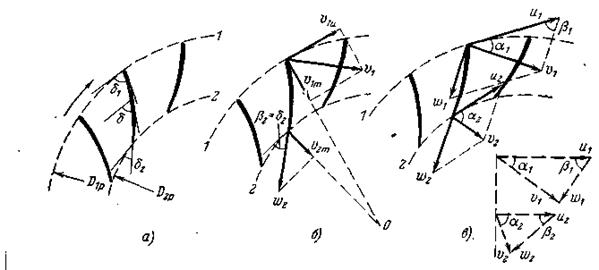
Рис. 12. Параллелограммы и треугольники скоростей
D1р и D2р - расчётные диаметры – расчётные диаметры входной I и выходной 2 кромки лопасти (как видно из рис.11, эти диаметры меньше номинального входного D1 и выходного D2).
Направление лопастей рабочего колеса в данной точке определяется углом 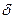 между касательной к средней линии профиля лопасти, и касательной к Dр, проведённой в сторону, обратную вращению колеса.
между касательной к средней линии профиля лопасти, и касательной к Dр, проведённой в сторону, обратную вращению колеса.
Условия работы турбины (режим) задаются двумя параметрами: расходом Q и частотой вращения рабочего колеса. При заданных размерах рабочего колеса это даёт возможность определить компоненты параллелограммов скоростей.
Переносная окружная скорость u выражается формулой
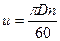 (6)
(6)
Проекция вектора абсолютной скорости на меридианную плоскость – меридианная составляющая vm (на рис. 11 показана v1m и v2m) приближённо может быть найдена из соотношения
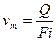 (7)
(7)
где Fi – суммарная площадь потока в колесе, нормальная к поверхности тока.
Другие необходимые компоненты берутся в зависимости от рассматриваемого сечения. Например, во входном сечении I рабочего колеса радиально-осевой турбины
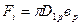 ,
,
где вр высота входного отверстия колеса и по (7)
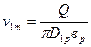 (8)
(8)
Окружная составляющая v1п зависит от от условий выхода потока из направляющего аппарата и по (4) будет равна (из закона постоянства момента скорости)
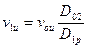 (9)
(9)
Абсолютная скорость на входе в колесо представляется векторной суммой (рис. 12, б)
V1 = V1m + V1u (10)
Зная V1 и по (6) 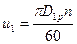 , строим параллелограмм скоростей и определяем W1 (рис. 12, в). Форма входного параллелограмма скоростей зависит от угла α1между u1 и v1и β1 между u1 и w1 (рис. 12, в).
, строим параллелограмм скоростей и определяем W1 (рис. 12, в). Форма входного параллелограмма скоростей зависит от угла α1между u1 и v1и β1 между u1 и w1 (рис. 12, в).
Часто вместо параллелограмма строят треугольник скоростей.
В выходном сечении рабочего колеса 2
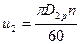 и
и 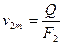 .
.
Кроме того, поскольку решётка лопастей рабочего колеса весьма густая, можно приближённо считать, что относительная скорость направлена по касательной к лопасти, т.е.
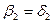 (11)
(11)
Из этого условия, согласно рис. 12 (б)
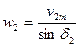 (12)
(12)
Имея U2 и W2 согласно (5) строим параллелограмм и находим V2 рис. (12,в). Форма выходного параллелограмма определяется углами α2 и β2.
Можно построить треугольники скоростей не только входного и выходного сечений, но и для промежуточных. Эти треугольники определят соответственно векторы Vi и по ним можно провести траектории абсолютного движения жидкости в рабочем колесе.
Вид такой траектории
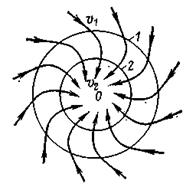
Рис. 13. Траектории абсолютного движения жидкости в радиально – осевой турбине
Следует обратить внимание на весьма важный вывод, что форма траекторий абсолютного движения не зависит от значения скорости v1, а определяется только её направлением.
Для осевых турбин поверхности тока в рабочем колесе близки к цилиндрическим (рис. 14,а) т.е.
D1р = D2р = Dр;
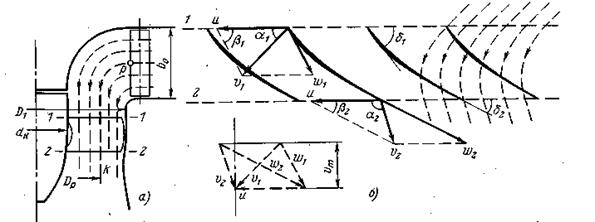
Рис. 14. Поток в осевой турбине
Расчётный диаметр можно вычислить как средний по площади
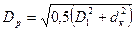 (13)
(13)
Развёртка цилиндрического сечения рабочего колеса показана на рис. 14 (б).
Особенность состоит в том, что
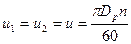 и
и 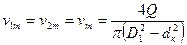
Скорость на входных кромках I определяется как векторная сумма
V1 = V1m + V1u
причём v1m находится по (9) – из закона постоянства момента скорости.
Абсолютная скорость V2 строится с учётом (11) и (12).
Треугольники скоростей на входной и выходной кромках совмещены, поскольку они имеют одинаковое основание u и высоту vm. Справа на рис. 14 (б) пунктирными линиями показаны траектории абсолютного движения жидкости в рабочем колесе.
- Выводы
Итак, построение параллелограммов скоростей даёт возможность определить скорости и углы при проектировании гидротурбин, которые аналитически определить сложно.
| <== предыдущая лекция | | | следующая лекция ==> |
| ветроэнергетики и биоэнергетики в мире | | | Режим работы турбины |
Дата добавления: 2016-04-14; просмотров: 1533;
