Баланс активных и реактивных мощностей
Активная мощность источников (турбогенераторов и гидрогенераторов электростанций, нетрадиционных источников, гидроаккумулирующих станций и др.) в любой момент времени соответствует потребляемой мощности (нагрузке) ΣPн:
∑Pн = ∑Pи + ∑Pсн + ∆Pп, (15.1)
где ΣPи – суммарная активная мощность источников; ΣРсн – собственные нужды генерирующих источников; ΔРп – потери активной мощности.
Приведенное уравнение определяет баланс активных мощностей в электрической системе.
Баланс активных мощностей соответствует определенным значениям частоты и напряжения в узлах, к которым подключены потребители (нагрузки). Изменение мощности источников связано с изменением частоты и напряжения очевидным равенством, получающимся разложением в ряд Тейлора функции ΣРн = F(f; U):
∆Pн = ϐ∑Pн / ϐf ∙ ∆f + ϐ∑Pн / ϐU ∙ ∆U. (15.2)
При нарушении баланса мощностей вследствие снижения генерирующей мощности или увеличения потребления активной мощности устанавливается режим с изменившимися значениями составляющих уравнения баланса мощности. Снижение генерируемой мощности приводит к уменьшению частоты и напряжения в системе и, наоборот, с увеличением мощности источников возрастают частоты тока и напряжения одинаково в любом узле электрической системы. Воздействовать на изменение частоты можно только изменением генерируемой активной мощности. На тепловых и гидравлических электростанциях это достигается увеличением или уменьшением выпуска энергоносителя, т. е. пара или воды.
Номинальное значение частоты в европейских странах составляет 50 Гц, в США и ряде других стран – 60 Гц. Снижение частоты приводит к уменьшению скорости вращения синхронных и асинхронных электродвигателей и, в конечном счете, к уменьшению производительности приводных механизмов.
В ориентировочных расчетах принимают, что изменение частоты на 1 % приводит к изменению активной мощности нагрузки на 0,5 %. Уравнение баланса реактивной мощности:
∑Qг + ∑Qс + ∑Qк = ∑Qн + ∑Qн +∑∆Qп, (15.3)
где ΣQг, ΣQc, ΣQк – реактивная мощность, генерируемая генераторами электростанций, компенсирующими устройствами (синхронными компенсаторами, конденсаторами и другими устройствами, а также емкостями воздушных и кабельных линий); ΣQн + ΣQсн + ΣΔQп – реактивная мощность, потребляемая нагрузками, а также собственными нуждами электроснабжения и обусловленная потерями в элементах систем электроснабжения.
Реактивная или обменная мощность существенно влияет на такие параметры систем электроснабжения, как потери мощности и энергии и уровни напряжения в узлах сети. Поэтому вопрос компенсации реактивной мощности относится к числу важнейших при проектировании и эксплуатации систем энергоснабжения предприятий. Как известно, величина (значение) реактивной мощности характеризует скорость обмена электромагнитной энергии источниками и потребителями электроэнергии. При этом индуктивные элементы являются накопителями реактивной мощности, а емкостные – ее генераторами. В трехфазных симметричных сетях реактивная мощность определяется как
Q = √3UIsinφ, (15.4)
в несимметричных сетях – суммой реактивных мощностей трех фаз:
Q = UAIAcosφA + UBIBcosφB + UCICcosφC. (15.5)
Полная (кажущаяся) мощность
S = √P2 + Q2, (15.6)
отношение мощностей:
Q / P =tgφ; P / S = cosφ
Приведенные выше формулы справедливы для сетей синусоидального тока, в которых нет высших гармоник.
Напомним основные формулы, которые используются в расчетах, связанных с реактивной мощностью. Потери активной мощности ΔР при передаче активной и реактивной мощностей по линии с сопротивлением R:
∆P = (P2 +Q2 / U2) ∙ R. (15.7)
Потеря напряжения
∆U = (PR +QX / U), (15.8)
где X – реактивное сопротивление линии.
При несинусоидальности напряжения и токов используется метод эквивалентных синусоид. Эквивалентные синусоиды напряжения Uэ и тока Iэ определяют по формулам:
n n
Uэ = √∑Uν2; Iэ = √∑Iν2; Sэ = Uэ Iэ, (15.9)
ν =1 ν =1
где Uv и Iv – соответственно напряжение и ток v-й гармоники. Реактивная мощность
Qэ = √ Sэ2 – Pэ2, (15.10)
n
где Pэ = √∑UνIνcosφ.
ν =1
Коэффициент мощности
cosφэ = Pэ / Sэ. (15.11)
При расчетах реактивной мощности вентильных преобразователей коэффициент мощности определяют по формуле
cosφэ = γicosφ1; (15.12)
значение cosφ1 находят по первым (основным) гармоникам напряжения и тока. Коэффициент искажения кривых тока
γi = I1 / Iэ. (15.13)
Обменные электромагнитные процессы можно рассматривать на основе разложения тока на составляющие: активную Iа, совпадающую по фазе с напряжением, и реактивную Ip, сдвинутую на угол π/2 (рис. 15.1):
I = Ia + Ip. (15.14)

|
| Рисунок 15.1 - Составляющие полного тока |
Очевидно, что составляющая Iа обусловливает активную мощность, а Iр – реактивную:
P = Ia2 R, (15.15a)
Q = Ip2 X. (15.15б)
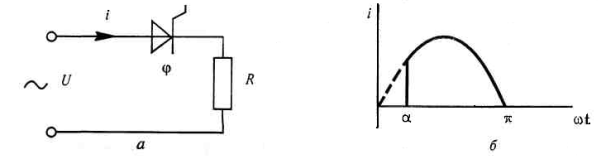
Этот подход удобен для понимания сущности энергетических процессов в системах электроснабжения с нелинейными нагрузками. В этом случае даже при отсутствии в сети реактивных элементов может иметь место Iр ≠ 0. Например, в простейшем случае одно- или двухполупериодного выпрямителя, работающего на активную нагрузку (рис. 15.2, а), при угле управления α ≠ 0 первая гармоника тока I1 сдвинута относительно кривой напряжения на угол φ1, значение которого зависит от угла управления α (рис. 15.2, б).
|
| Рисунок 15.2 - Схема одно- или двухполупериодных выпрямителей, работающих на активную нагрузку (а) и сдвиг первой гармонии при α ≠ 0 (б) |
Ток первой гармоники может быть представлен суммой активной и реактивной составляющих по выражению (15.14), соответственно могут быть представлены мощности по выражениям (15.15а). Однако мощность, определяемая выражением (15.15б), не связана с обменными процессами, она обусловлена лишь наличием сдвига по фазе между током и напряжением. Ее правильнее было бы назвать мощностью сдвига. В дальнейшем изложении, однако, мы будем пользоваться привычным и общепринятым термином «реактивная мощность» вне зависимости от причины, вызывающей появление реактивной составляющей тока.
Отметим весьма важное обстоятельство: компенсация реактивной мощности (т. е. ее минимизация) производится одними и теми же методами вне зависимости от природы ее появления, т. е. наличия реактивных элементов в сети или сдвига фаз, обусловленного нелинейными потребителями. На практике обычно имеет место сочетание обеих причин: в вентильных преобразователях (выпрямителях, инверторах и др.) используются реакторы для сглаживания коммутационных процессов и батареи конденсаторов; преобразователи и ДСП включаются через трансформаторы и т. д.
Следует иметь в виду, что более точно коэффициент мощности cos φ следовало бы назвать коэффициентом сдвига фаз.
Согласно второму закону электромеханики все электрические машины обратимы, т. е. они могут работать как в двигательном, так и в генераторном режимах. Это свойство электрических машин используется, в частности, на гидроаккумуляторных станциях: синхронная машина используется в качестве двигателя при перекачке воды в резервуары в периоды минимальных нагрузок энергосистемы и в генераторном режиме, когда запасенная потенциальная энергия воды используется для вращения гидротурбины.
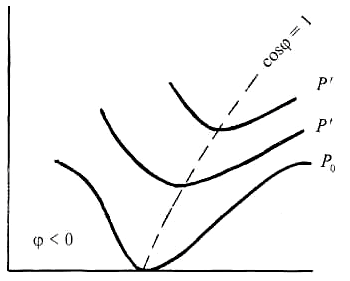
Синхронные машины, применяемые в промышленных системах электроснабжения, вне зависимости от их основного назначения (электродвигатели, генераторы) используются также в качестве источников реактивной мощности РМ. Синхронные компенсаторы устанавливают исключительно с целью получения РМ. Естественно, что эти машины могут работать также в режиме потребления РМ. Это можно наглядно продемонстрировать с помощью известных U-образных характеристик. На рис. 15.3 представлены U-образные характеристики синхронного генератора, подключенного к электрической сети с неизменным уровнем напряжения U0 = const при различных значениях активной нагрузки Р = 0, Р', Р" (I – ток статора; If – ток возбуждения).
|
| Рисунок 15.3 - U-образные характеристики синхронного генератора (U0 = const, активная нагрузка Р = 0, Р', Р") |
При значениях тока возбуждения, меньших граничного (If < Ifгр), т. е. в режиме недовозбуждения, синхронная машина «ведет себя» как индуктивность, т. е. потребляет реактивную мощность; при перевозбуждении (If > Ifгр) она является источником реактивной мощности, т. е. «ведет себя» как емкость.
Для синхронных электродвигателей значения Р, Р', Р" являются электромагнитной мощностью, соответствующей вращающему электромагнитному моменту. Нижняя кривая – U-образная характеристика синхронного компенсатора.
Синхронные компенсаторы, в отличие от синхронных генераторов, не имеют выходного конца вала, это облегчает герметизацию машины и позволяет использовать водородное охлаждение. Компенсаторы выпускают на напряжения 6,6–15,75 кВ и мощностью до 345 МВА.
Полная номинальная мощность компенсатора при работе с перевозбуждением, в генераторном режиме, определяется по формуле
Sном = √3Uном ∙ Iном (15.16)
Полная мощность при недовозбуждении (потребляемая)
Sном = √3Uном2 / Xd. (15.17)
Значение синхронного индуктивного сопротивления синхронного компенсатора (в относительных единицах) Xd= 1,8–5–2,5.
Активная мощность, обусловленная наличием механических потерь, а также потерь в стали и меди, составляет 1–2 % номинальной мощности.
Синхронные компенсаторы иногда применяют на главных понизительных подстанциях (ГПП) предприятий.
Дата добавления: 2016-02-11; просмотров: 3075;
