ОТКЛОНЕНИЯ РАСПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
Отклонением расположения поверхности или профиля называют отклонение реального расположения поверхности (профиля) от его номинального расположения. Количественно отклонения расположения оцениваются в соответствии с определениями, приведенными ниже. При оценке отклонений расположения отклонения формы рассматриваемых поверхностей (профилей) и базовых элементов должны исключаться из рассмотрения. При этом реальные поверхности (профили) заменяются прилегающими, а за оси, плоскости симметрии и центры реальных поверхностей (профилей) принимают оси, плоскости симметрии и центры прилегающих элементов.
Из-за многообразия видов расположения поверхностей и соответственно видов отклонений расположения рассмотрим только некоторые примеры.
| Рис.4.4. Отклонения расположения поверхностей |
| Рис. 4.5. Отклонения от параллельности и перекос осей. |
| Рис. 4.6. Отклонения от соосности |
| Рис. 4.5. Отклонения от соосности. |
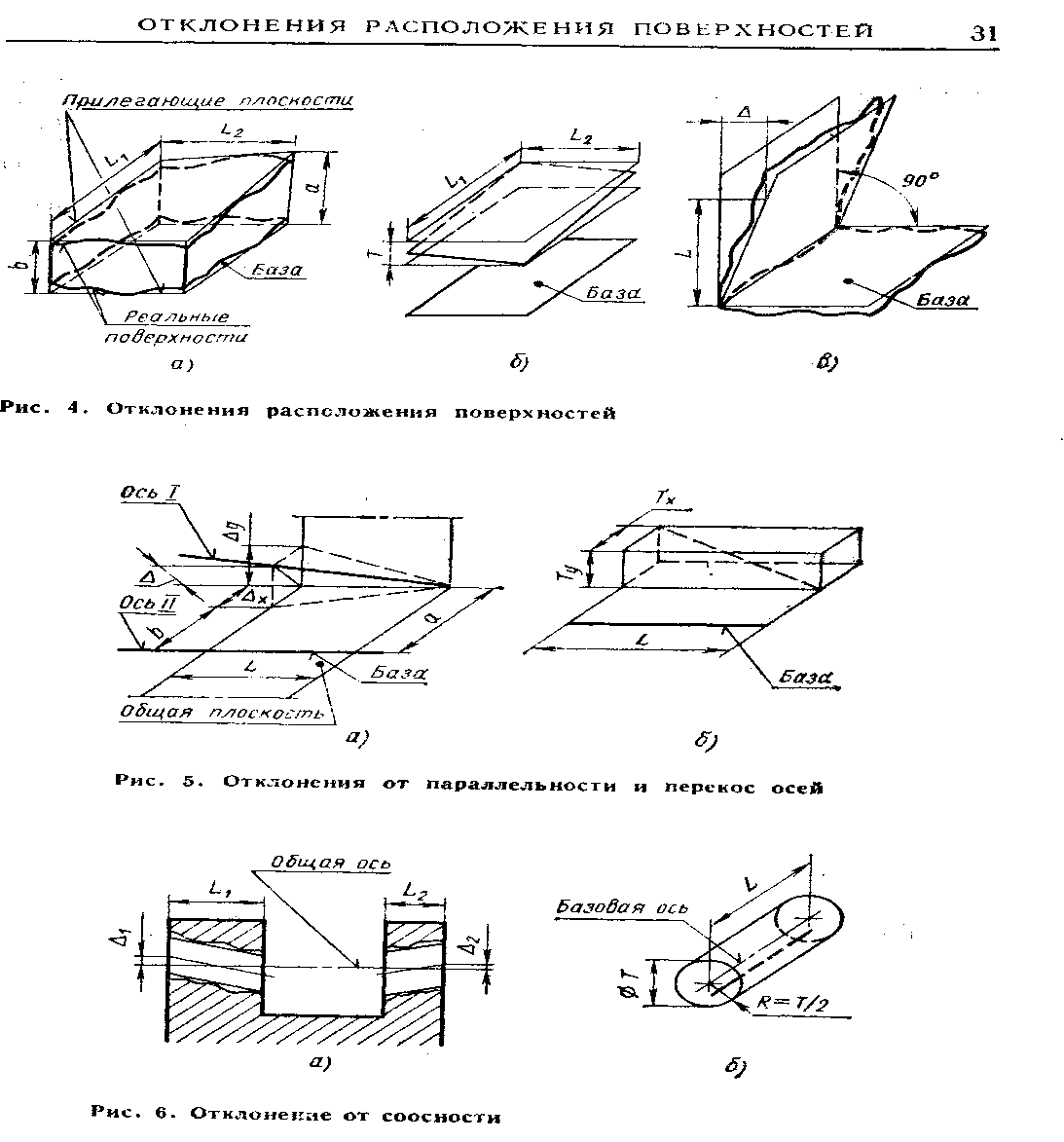
Полем допуска параллельности плоскостей называют область в пространстве, ограниченную двумя параллельными плоскостями, отстоящими друг от друга на расстояние, равное допуску параллельности Т, и параллельными базовой плоскости (рис. 4.4. б).
Отклонение от перпендикулярности плоскостей показано на рис. 4.4.в.
Отклонение от параллельности осей (или прямых) в пространстве
геометрическая сумма D = Ö D2x + D2y отклонений от параллельности проекций осей (прямых) в двух взаимно перпендикулярных плоскостях. Одна из этих плоскостей является общей плоскостью осей, т. е. плоскостью, проходящей через одну (базовую) ось и точку другой оси (рис. 4.5, а). Отклонение от параллельности осей (или прямых) в общей плоскости обозначено через перекос осей (или прямых) обозначен через Dx = а - б. Перекос осей (или прямых) обозначен Dy
Поле допуска параллельности осей (или прямых) в пространстве — это область в пространстве, ограниченная прямоугольным параллелепипедом, стороны сечения которого равны соответственно допуску параллельности осей (прямых) в общей плоскости Тх и допуску перекоса осей (прямых) Ту, а боковые грани параллельны базовой оси и соответственно параллельны и перпендикулярны общей плоскости осей (рис. 4.5.б). Поле допуска может быть представлено также цилиндром, диаметр которого равен допуску параллельности Т, а ось параллельна базовой оси.
Отклонение от соосности относительно общей оси — это наибольшее расстояние (D1; D2) между общей осью двух или нескольких поверхностей вращения и осью рассматриваемой поверхности вращения на длине нормируемого участка (рис. 4.6.а). Допуск соосности в диаметральном выражении равен удвоенному допустимому значению отклонения от соосности и в радиусном выражении — наибольшему допустимому Значению отклонения. Полем допуска соосности является часть пространства, ограниченная цилиндром, диаметр которого равен допуску соосности в диаметральном выражении Т или удвоенному допуску соосности в радиусном выражении R, а ось совпадает с базовой осью (рис. 4.6.б).
Двоякая количественная оценка соосности (в диаметральном и радиусном выражениях) принята по рекомендации ISO также для симметричности и пересечения осей. Ранее эти отклонения определялись только в радиусном выражении.
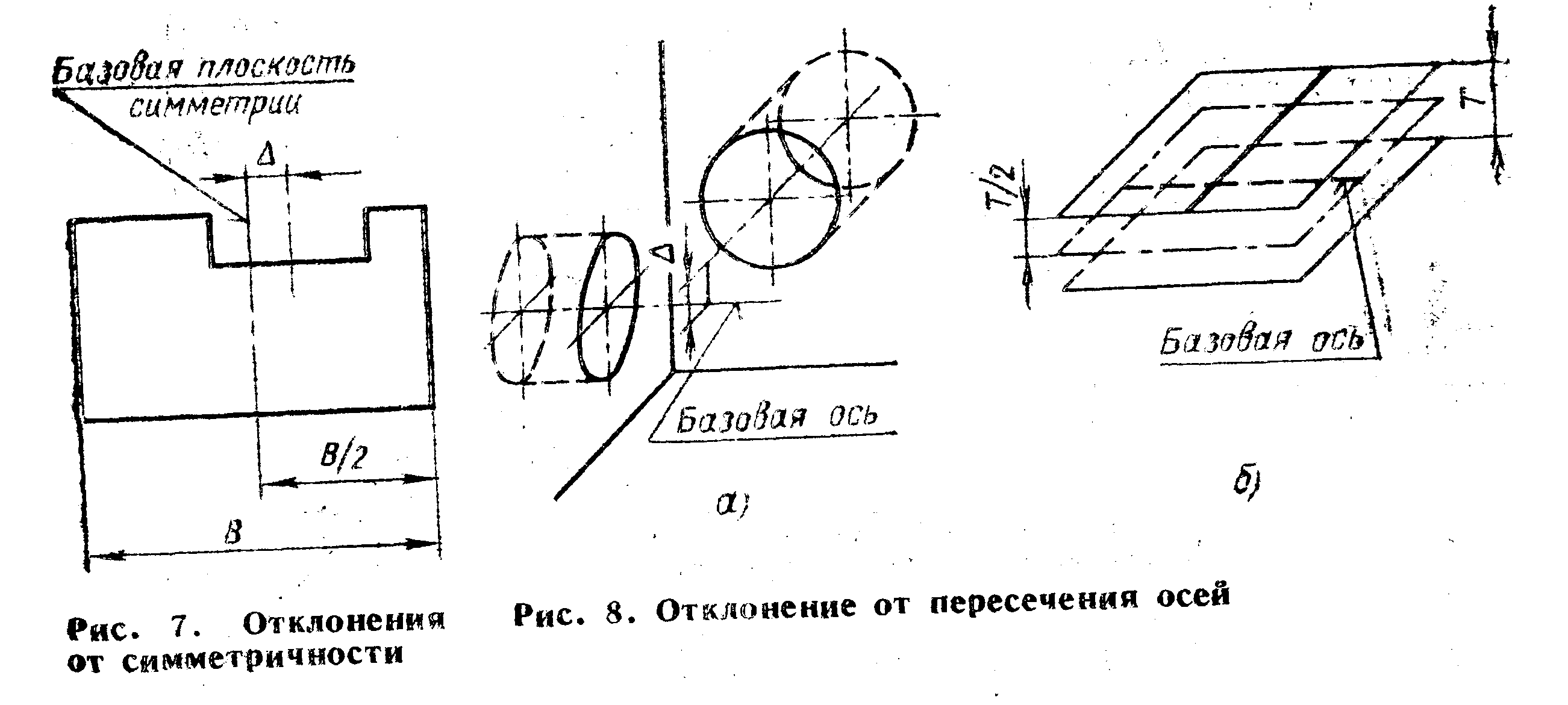
Отклонение от симметричности относительно базовой плоскости - наибольшее расстояние D между базовой плоскостью симметрии рассматриваемой поверхности и реальной плоскостью симметрии в пределах нормируемого участка (рис.4.7). Отклонение от пересечения осей — меньшее расстояние D между осями, номинально пересекающимися (рис.4.8, а). Поле допуска пересечения определяется частью пространства, ограниченного двумя параллельными плоскостями, отстоящими друг от друга на расстояние, равное допуску пересечения в диаметральном выражении Т или удвоенному допуску пересечения в радиусном выражении Т/2, и расположенными симметрично относительно базовой оси (рис. 4.8, б).
|
| Рис. 4.7. Отклонение от симметричности |
| Рис. 4.8. Отклонение от пересечения осей |
Вместо термина смещение оси (или плоскости симметрии) от номинального расположения» введены краткие термины «Позиционное отклонение», «позиционный допуск».
Дата добавления: 2016-04-14; просмотров: 1409;
