Алгоритм трассировки лучей

Идея:

Есть источник, свет от источника падает на объект, поступает к наблюдателю (отразившийся от поверхности объекта). Однако не многие из лучей источника дойдут до наблюдателя. Сколько лучей учитывать? - избыточность

Идея Аппеля: отслеживать (трассировать) луч в обратном направлении от наблюдателя к объекту через точки растра.

Упрощения:

1. Объект преобразован в с.к. изображения.

2. От центральной проекции переходим к параллельной (точка наблюдения стремится к бесконечности по z):

- все лучи параллельны оси z

- каждый луч проходит через пиксель на экране до объекта

Алгоритм

Для каждого луча отслеживаем, какие грани объекта имеют с ним пересечение, проверяется пересечение луча с каждой из граней, получаем точку пересечения. Точки пересечения сортируются по глубине (по z).

Точка пересечения с zmin – видимая поверхность для данного пикселя.

Атрибут этой точки грани = характеристике пикселя.

Основная задача: определить точку пересечения (75-90% времени)=> объект должен состоять из таких граней, для которых можно найти точку пересечения (треугольники, многоугольники).

1. Поиск точек пересечения с плоскостью грани.

т.к. лучи параллельны z => точки пересечений можно искать с проекциями по экранную плоскость (используя те же координаты X, Y)

=> координаты точек пересечения (Xп, Yп) = (x, y) пикселя, через который проходит луч. Координата 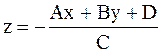, где A, B, C, D – коэффициенты уравнения плоскости, содержащей грань.

A=(y2-y1)(z3-z1)-(y3-y1)(z2-z1)

B=(z2-z1)(x3-x1)-(z3-z1)(x2-x1)

C=(x2-x1)(y3-y1)-(x3-x1)(y2-y1)

D= -Ax1-By1-Cz1

2. Определить имеет ли грань пересечение с лучом.

а) вводят оболочку, с которой можно легко найти пересечение (окружность, прямоугольник)

Окружность: центр О(x, y), R через P1, P2, P3

Прямоугольник: Xmin, Xmax, Ymin, Ymax.

Определяем пересечение

Окружность: рассчитываем расстояние S от центра окружности О(Xo, Yo) до точки Pп(Xп, Yп). Если S≤R => пересечение с оболочкой есть.

Прямоугольник: осуществляем перенос, при котором точка пересечения P – начало координат (луч=осьZ). Т(–Xп, –Yп).

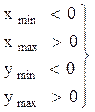
При выполнении всех этих условий точка пересечения трассирующего луча с гранью находится в прямоугольной оболочке грани

б) если есть пересечение с оболочкой, определим лежит ли точка в треугольнике.

Площадь треугольника.

S = |x1y2-x2y1 + x2y3-x3y2 + x3y1-x1y3| / 2.

В формуле присутствует знак модуля. Знак выражения, стоящего под модулем отвечает за ориентацию треугольника, то есть за то, в каком порядке перечислены вершины треугольника. Если значение выражения под модулем положительно, то точки перечислены против часовой стрелки, если отрицательно — по часовой стрелке.

Точка D лежит внутри треугольника ABC только тогда, когда все 3 треугольника ABD, BCD и CAD (именно с таким порядком вершин!) имеют одинаковую ориентацию. Считаем выражения для площадей этих треугольников (без модулей) и сравниваем их знаки.

Если в описании граней единичного выпуклого замкнутого объекта все вершины перечислены в порядке, например, против часовой стрелки, то для определения видимости грани необходимо вычислить ее текущую ориентацию в г. с. к., и если она не совпадает с описанной (т. е. не против часовой стрелки), то грань не выводится (метод ориентации грани: лицевая/нелицевая). Этот метод очень прост, но не учитывает экранирование грани другой гранью объекта, а только ее ориентацию «к наблюдателю»/«от наблюдателя».

Достоинства метода трассировки лучей:

1. Включает в себя растровую развертку

2. Легко можно учитывать модель освещения
(включая прозрачность, фактуру и т.д.)

3. Слабо зависит от числа граней.

Недостатки:

1. Медленный поиск точки пересечения луча с гранью.

2. Быстродействие зависит от разрешения экрана.