Ньюэл М., Ньюэл Р., Санча

1. Упорядочить все многоугольники в соответствии с max Z-координаты. {P}

2. Разрешить все неопределенности с Z-оболочками => сформировать окончательный список.

3. Преобразовать каждый из многоугольников в растровую форму в порядке убывания Z-координаты (можно методами заполнения) в соответствии с правилами закраски.

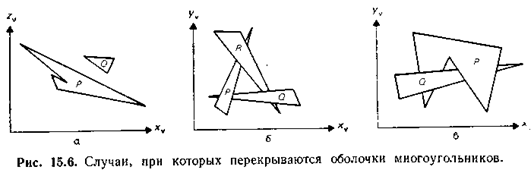
Неопределенности

Алгоритм проверки: для простоты будем считать, что рассматривается параллельное проектирование вдоль оси Oz.

Перед выводом грани Р следует убедиться, что никакая другая грань Q, проекция которой на ось Oz пересекается с проекцией грани Р, не может закрываться гранью Р. И если это условие выполнено, то грань Р должна быть выведена раньше. Предлагаются следующие 5 тестов в порядке возрастания сложности проверки (хотя бы один «нет» и переход к след. паре граней):

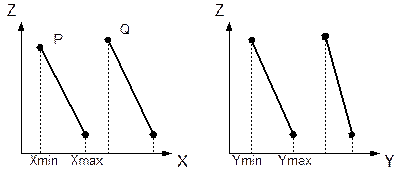1. Пересекаются ли проекции этих граней на ось Ох?

X-оболочки не перекрываются => многоугольники также не перекрываются

2. Пересекаются ли их проекции на ось Оу?

Y-оболочки не перекрываются

(PXmax<QXmin) or (PXmin>QXmax) (PYmax<QYmin) or (PYmin>QYmax)

3. Находится ли грань Р по другую сторону от плоскости, проходящей через грань Q, чем начало координат (наблюдатель)?

P целиком лежит со стороны от плоскости Q, которая дальше от точки зрения (наблюдения)

4. Находится ли грань Q по ту же сторону от плоскости, проходящей через грань Р, что и начало координат (наблюдатель)?

Q лежит со стороны плоскости, содержащей P, которая ближе к точке наблюдения

Уравнение плоскости Ax+By+Cz+D=0 заданной тремя точками P1, P2, P3.

A=(y2-y1)(z3-z1)-(y3-y1)(z2-z1)

B=(z2-z1)(x3-x1)-(z3-z1)(x2-x1)

C=(x2-x1)(y3-y1)-(x3-x1)(y2-y1)

D= -Ax1-By1-Cz1

С какой стороны от плоскости находится точка?

P4(x4,y4,z4), P5(x5,y5,z5)

fТ=Ax+By+Cz+D

fТ>0 – точка лежит дальше от плоскости к точке наблюдения;

fТ<0 – точка лежит ближе к плоскости к точке наблюдения;

fТ=0 – точка лежит на плоскости.

5. Пересекаются ли проекции этих граней на картинной плоскости?

Проекции P и Q на плоскости XY не пересекаются

Задача: С какой стороны от прямой лежит точка?

Уравнение прямой через две точки

=>

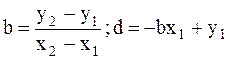
y=bx+d

тогда fТ=y–bx–d

fТ>0 – выше, правее (дальше);

fТ<0 – ниже, левее (ближе);

fТ=0 – лежит на прямой.

Задача: Пересекаются ли 2 ребра? è

Задача Пересекаются ли 2 многоугольника?

Каждое ребро одной грани сравнить с каждым ребром другой. Если найдены 2 пересекающихся ребра => многоугольники пересекаются.

Если хотя бы на один из этих вопросов получен отрицательный ответ, то считаем что эти две грани - Р и Q упорядочены верно, и сравниваем Р со следующей гранью. В противном случае считаем, что эти грани необходимо поменять местами, для чего проверяются следующие тесты:

3'. Находится ли грань Q по другую сторону от плоскости, проходящей через грань Р, чем начало координат?

4'. Находится ли грань Р по ту же сторону от плоскости, проходящей через грань Q, что и начало координат?

В случае если ни один из этих тестов не позволяет с уверенностью решить, какую из этих двух граней нужно выводить раньше, то одна из них разбивается плоскостью, проходящей через другую грань. В этом случае вопрос об упорядочении оставшейся грани и частей разбитой грани легко решается.