Кейнсианская функция сбережений. Неоклассические функции потребления и сбережений.
Кейнсианская функция сбережений.
Как известно (глава 3), домашние хозяйства используют располагаемый доход на потребление C и образование личных сбережений S:
Y = C + S
Следовательно, функцию сбережений можно получить, вычитая функцию потребления из Y:
S = Y – C,где
C = Ca + MPC×Y,
S = Y – Ca - MPC×Y
S = - Ca + (1 – MPC)Y.
1 – MPC = MPS (предельная склонность к сбережению).
МРS - предельная склонность к сбережению - представляет собой долю прироста дохода, на величину которой увеличиваются сбережения:
МРS = 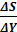
Тогда функцию сбережений можно записать:
S = - Ca + MPS×Y (2)
Так как C + S = Y, то MPC + MPS = 1.
Графическая интерпретация взаимосвязи функции потребления и функции сбережений представлена на рисунке 4.5.
Для того чтобы правильно изобразить взаимосвязь графика потребления C и графика сбережений S, надо иметь в виду, что функции потребления и сбережений выводятся для всей совокупности домашних хозяйств, то есть это агрегированные функции. Это означает, что при существующейв капиталистической экономике структуре распределения дохода предельная склонность к потреблению выше, чем предельная склонность к сбережению.
Рис. 4.5
C,S
C = Ca + MPC×Y
MPC
Ca S = - Ca + MPS×Y
-Ca MPS Y0 Y
Начинаем с воспроизведения графика функции потребления Cна рисунке 4.1 (с. 9). Затем проводим биссектрису угла 0. Поскольку угол наклона кривой потребления меньше угла наклона биссектрисы, эти линии пересекутся. Опустив перпендикуляр из точки пересечения на горизонтальную ось, получаем значение располагаемого дохода Y0.
Y0 называется пороговым уровнемрасполагаемого дохода. Это такое значение располагаемого дохода Y, при котором весь доход потребляется, а значит, сбережения равны нулю.
Таким образом, мы получаем точку (с координатами Y = Y0; S = 0), через которую пройдет кривая сбережений. Вторую точку этой кривой мы получим, отложив на вертикальной оси вниз от 0 отрезок равный Ca. Проведя линию через две эти точки, мы получим кривую сбережений S. Если все сделано правильно, мы получим две расходящиеся линии, изображающие функции потребления и сбережений.
Рис. 4.6
C
C = Ca + MPCY
Ca
Y1 Y0 Y2 Y
Рисунок 4.6 представляет, как по мере роста располагаемого дохода и, следовательно, национального дохода, изменяется соотношение между уровнем потребления и уровнем сбережений:
· Y = Y0 Þ C = Y Þ S = 0
· Y < Y0 Þ C > Y Þ S < 0(отрезок, отмеченный зеленой фигурной скобкой больше отрезка, отмеченного черной скобкой; сбережения представляют собой отрицательную разницу между потреблением и доходом – синий вертикальный отрезок).
· Y > Y0 Þ C < Y Þ S > 0(сбережения представлены красным вертикальным отрезком).
Следовательно, чем больше уровень располагаемого доходаY при данной предельной склонности к потреблению, тем больше уровень личных сбережений домашних хозяйств.
Под воздействием ряда факторов (изменение богатства, задолженности, уровня цен, ожиданий и т.п.) кривые потребления и сбережений смещаются в противоположных направлениях.
В заключение отметим, что если мы вводим в анализ государственный сектор, то график и уравнение функции потребления принимает следующий вид (рисунок. 4.7):
Рис. 4.7
C C = Ca+MPC(1–t)Y
MPC(1-t)
Ca
0 Y
где Y – национальный доход
Если включим в рассмотрение государство, то Y – национальный доход:
 = Y – Т(чистые налоги)
= Y – Т(чистые налоги)
T = TX – TR (налоги минус трансферты)
 = t (чистая ставка налогообложения)
= t (чистая ставка налогообложения)
T = tY
 = Y – tY
= Y – tY
 = Y(1 – t )
= Y(1 – t )
C = Ca + MPC × Y(1 – t)
Надо отметить, что изменение графика показывает уменьшение угла наклона кривой потребления: чем выше ставка налогообложения t, тем меньше угол наклона при данном значении MPC. Однако Кейнс считал, что изменение ставки налогообложения, если оно способствует более справедливому распределению дохода, может обусловить рост предельной склонности к потреблению, что очень важно иметь в виду для формирования бюджетно-налоговой политики.
Неоклассические функции потребления и сбережений.
Неоклассическая школа, продолжая традиции классической школы микроэкономического анализа, исследует поведение индивидуального (репрезентативного) домашнего хозяйства, обобщая полученные результаты анализа на все домашние хозяйства.
В концепции неоклассической школы сбережениядомашнего хозяйства являются возрастающей функцией от ставки процента(рисунок 4.8 А), следовательно, функция потребления – убывающей функцией(рисунок 4.8 Б):
S(r) = = - C0 + Y×a×r
C(r) = Y – S = Y + C0 - Y×a×r = C0 + Y(1 - a×r),
где
C0– независимый от процентной ставки уровень потребления,
Y – располагаемый доход (задан экзогенно),
r - ставка процента,
a -параметр, показывающий, на сколько единиц сократится потребление ( = возрастут сбережения ), если процентная ставка увеличится на 1 процентный пункт.
Неоклассическая точка зрения на потребление и сбережения, по мнению многих экономистов, не нашла практического подтверждения. Это не означает, что процентная ставка не оказывает влияния на потребление и сбережения, но это влияние, по мнению Кейнса, несущественно: «применительно к короткому периоду влияние нормы процента на индивидуальное потребление при данном уровне дохода следует признать второстепенным и сравнительно небольшим» (Кейнс, с. 115).
Рис. 4.8А Б
r r
S(r) C(r)
- C0 0 S 0 C0 C
И еще небходимо отметить следующий момент. Во всех неоклассических моделях используется реальная процентная ставкаr. Это на самом деле связано с тем, что, по мнению неоклассиков экономические агенты не испытывают денежной иллюзии и способны быстро учитывать изменения уровня цен в процессе принятия решений. То есть они ориентируются на реальную процентную ставку, фактически руководствуясь эффектом Фишера:
r = i – πe
(Это уравнение применимо, если инфляция не превышает 10%)
Общий вид уравнения, связывающего rиi, выглядит следующим образом:
 = r
= r
Поскольку в кейнсианском анализе цены (уровень цен) являются экзогенным фактором (т.е. P = const.), все номинальные переменные выступают в реальном выражении, в том числе и текущая ставка (норма) процентаi. Это особенно важно иметь в виду при анализе инвестиционной функции, которой посвящена следующая лекция.
Дата добавления: 2016-04-14; просмотров: 1459;
