Функции распределения в математической статистике.

2.6.1. Распределение хи-квадрат ( )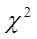

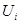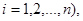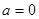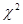Случайная величина, представляющая собой сумму квадратов n независимых случайных величин ( каждая из которых подчиняется нормальному закону распределения с математическим ожиданием и дисперсией , называется случайной величиной, распределенной по закону (“хи - квадрат”) с степенями свободы:

(*)

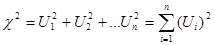Число степеней свободы обозначает число независимых слагаемых суммы 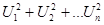, образующих переменную с распределением 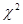. Если в выражении (*) все n слагаемых независимы, то число степеней свободы .

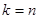Пусть независимые нормально распределенные случайные величины с математическим ожиданием и дисперсией 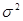. Положив в выражении (*), что 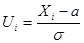получим случайную величину

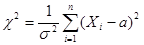
распределенную по закону 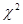с n степенями свободы.

Примем без доказательства, что случайная величина 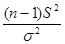имеет распределение 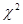с с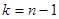тепенями свободы.

Распределение вероятностей величины 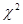является непрерывным и ассиметричным (рис. 17). Оно определяется одним параметром - число степеней свободы . Число степеней свободы должно составлять, по меньшей мере, 1. Чем больше , тем более симметрично распределение 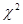. С увеличением числа степеней свободы распределение медленно приближается к нормальному, хотя некоторая правосторонняя асимметрия проявляется постоянно.

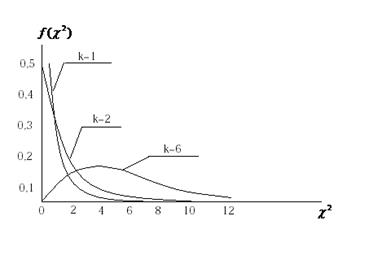
Рис.17 Функция 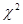распределения в зависимости от числа степеней свободы k.

Математическое ожидание случайной величины с распределением 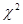и степенями свободы равно числу степеней свободы.

Дисперсия случайной величины с распределением 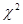и степенями свободы равна удвоенному числу степеней свободы.

Дифференциальная функция распределения 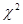сложна и интегрировать ее является весьма трудоемким процессом, поэтому созданы специальные таблицы распределения 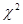(см. приложение 4). По таким таблицам, для требуемой по условиям опыта доверительной вероятности (уровня значимости) и числу степеней свободы, находят критическое значение 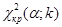, для которого выполняется условие 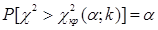(вероятность того, что случайная величина 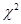превысит значение 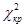равна уровню значимости 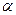). Значение 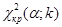является границей некоторой критической области определяемой неравенством . Например, для числа степеней свободы 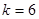и 95% доверительной вероятности (уровень значимости 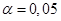) критическое значение 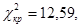т.е. для выбранного уровня доверительной вероятности случайная величина 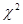, найденная по выборке объема n, должна быть меньше 12,59. На рис. 17 графически показаны доверительная вероятность, уровень значимости и значение 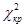, соответствующие этому примеру.

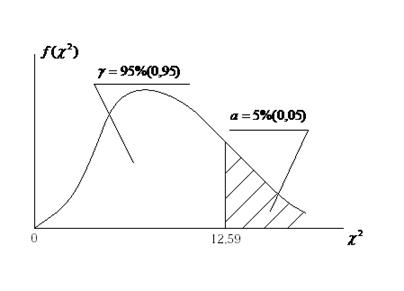
Рис. 17. 95% доверительная вероятность и 5% уровень значимости для

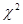распределения.

Чтобы разобраться с понятием критической области, необходимо, хотя бы коротко, определить такие понятия, как нулевая и конкурирующая гипотезы, статистический критерий.