2 страница. Вопросы для самопроверки
Вопросы для самопроверки
6. С какой целью выполняется преобразование чертежа с применением способа замены плоскости проекций?
7. Какие две из трех плоскостей проекций можно взять в качестве базовой системы плоскостей проекций?
8. С помощью какой линии на чертеже изображают новую систему плоскостей проекций?
9. Расстояние от объекта до какой плоскости из двух, формирующих базовую систему плоскостей, при использовании проецирования в дополнительную плоскость проекций остается неизменным?
10. Какое направление имеет линия связи в новой системе плоскостей проекций?
| 11. Какое главное требование к расположению дополнительной плоскости проекций относительно неизменной плоскости проекций? 12. Какой из параметров точки (широта, глубина или высота) остался неизменным в случае замены плоскости проекций, показанном на рис. 7.6? 13. Какому отрезку равняется расстояние от точки А до дополнительной плоскости проекций П4 (рис. 7.6). | 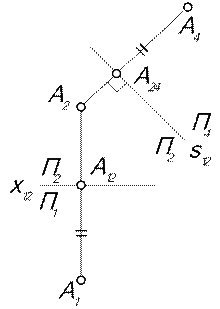
| |
| Рис.7.6 | ||
| 14. Какую из сторон треугольника (АВ, ВС или АС) можно превратить в проецирующую, сделав замену только одной плоскости проекций (рис. 7.7)? 15. Угол наклона прямой линии, к которой из плоскостей проекций можно определить на дополнительной плоскости проекций, если в базовой системе плоскостей проекций неизменной осталась фронтальная плоскость проекций? | 
| |
| Рис. 7.7 | ||
| 8. МНОГОГРАННИКИ Многогранником называют геометрическое тело, со всех сторон ограниченное плоскостями. Элементами многогранника являются грани, ребра и вершины. Все ребра многогранника в совокупности образуют так называемую сетку. Наиболее распространенными в практике являются пирамиды, призмы и правильные многогранники. Пирамида – многогранник, все грани которого, кроме одной – основания, имеют общую вершину, которую называют вершиной пирамиды (рис. 8.1а). Основание может быть произвольным многоугольником, все же боковые грани пирамиды – треугольники. Призма – многогранник, который имеет взаимно параллельные боковые ребра (рис. 8.1б). Боковые грани призмы – параллелограммы; две грани, которые не параллельны боковым ребрам, являются основаниями призмы в виде произвольных равных многоугольников. Если боковые ребра перпендикулярны основаниям, призма называется прямой, если нет – наклонной. Основания призмы могут быть не параллельными между собой, тогда такую призму называют усеченной. | ||
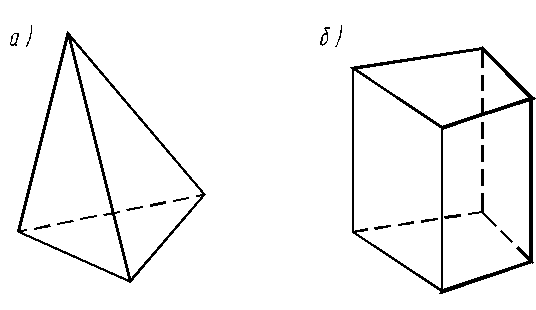
| ||
| Рис. 8.1 | ||
| Если весь многогранник располагается по один бок плоскости любой его грани, он называется выпуклым (рис. 8.1), если нет – вогнутым. В дальнейшем рассматриваются только выпуклые многогранники. Если основаниями пирамиды или призмы является правильный многоугольник, такие поверхности называют правильными пирамидой или призмой. Правильные выпуклые многогранники (тела Платона) – те многогранники, все грани которых являются конгруэнтными правильными многоугольниками. Различают пять правильных многогранников: - тетраэдр (четырехгранник) – все грани его равносторонние треугольники; - гексаэдр (шестигранник) – все грани – квадраты; - октаэдр (восьмигранник) – все грани являются равносторонними треугольниками; - додекаэдр (двенадцатигранник) – все грани являются правильными пятиугольниками; - икосаэдр (двадцатигранник) – все грани – равносторонние треугольники. 8.1. Изображение многогранника на чертеже На комплексном чертеже многогранники изображаются проекциями своих вершин и ребер (сетки) с учетом видимости их на плоскостях проекций. На рис. 8.2 показаны проекции пирамиды (рис. 8.2а) и наклонной призмы (рис. 8.2б). | ||
| ||
| Рис. 8.2 | ||
| Задача. Построить проекции многогранника по заданным вершинам. Найти недостающие проекции точки М, которая принадлежит поверхности многогранника (рис. 8.3). | ||

| ||
| Рис. 8.3 | ||
| Алгоритм решения 1. Построив профильные проекции вершин пирамиды, соединяем одноименные проекции вершин отрезками и получаем проекции пирамиды. Видимость ребер и граней определяем по представлению. На П1 видимы боковые ребра и грани пирамиды, так как вершина S располагается над основанием АВС. Рассматривая горизонтальную проекцию совместно с направлением на П2, определяем, что видимыми на П2 являются грани ASB и BSС, а грань АSC и ее ребро АС – невидимы. Аналогичным образом определяем, что на П3 невидимыми являются ребра, прилегающие к вершине С. | ||
| 2. Строим недостающие проекции точки М, принадлежащей пирамиде, используя признак принадлежности точки гранной поверхности: точка принадлежит поверхности многогранника, если лежит на прямой, которая принадлежит какой-либо грани этой поверхности. Точка М видима на П2 (ее проекция не заключена в скобки), следовательно, она лежит в грани ASB. Проводим в этой грани через М2 произвольную прямую, например, S212 и строим остальные проекции прямой и по принадлежности им находим недостающие проекции точки. Так как грань ASB видима на всех проекциях, то и точка М везде является видимой. | ||
| 8.2. Пересечение многогранника плоскостью | ||
| При пересечении многогранника плоскостью получают многоугольник, вершины которого – точки пересечения ребер многогранника с секущей плоскостью, а стороны – линии пересечения его граней с той же плоскостью (рис. 8.4). Количество вершин многоугольника совпадает с количеством ребер, которые пересекаются. Решение этой задачи можно осуществить двумя способами: - способом ребер – решая первую основную позиционную задачу столько раз, сколько ребер пересекаются плоскостью; - способом граней – решая вторую основную позиционную задачу. Более удобным в построении является способ ребер. | 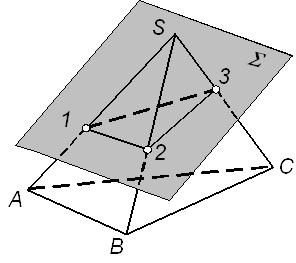 Рис. 8.4 Рис. 8.4
| |
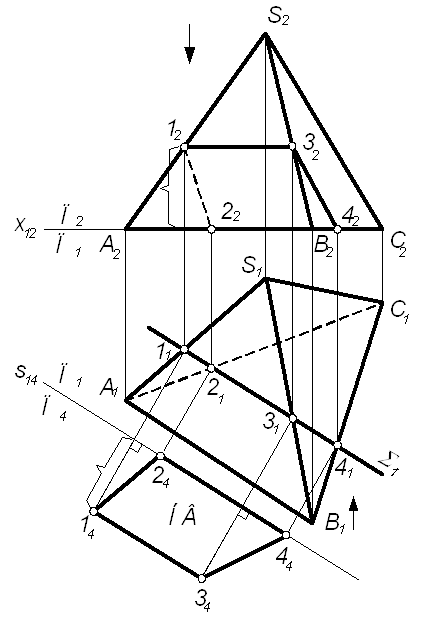
| Задача. Построить проекции и натуральную величину сечения пирамиды SАВС плоскостью S (S1) (рис. 8.5). | ||
Алгоритм решения
1. Так как S – горизонтально-проецирующая плоскость, то отрезок ее вырожденной проекции S1, что лежит внутри очерка пирамиды – горизонтальная проекция сечения. Вершины сечения сначала находим на П1, как результат пересечения S1 с проекциями ребер, а затем на других плоскостях проекций – по принадлежности ребрам.
2. Найденные вершины сечения соединяем отрезками, руководствуясь правилом: отрезками прямых можно соединять только точки, которые лежат в одной грани многогранника.
3. НВ сечения определяем способом замены плоскостей проекций: П2 →П4 || S, П1 / П2 (x12)→ П1 / П4 (s14 || S1).
4. Видимость на чертеже определяем по представлению. Из двух скрещивающихся ребер SB и АС при взгляде сверху ближе к наблюдателю SB, потому АС на П1 невидимо. На П2 невидимой является грань ASC и принадлежащая ей сторона сечения (12).
| ||
| Рис. 8.5 | ||
| 8.3. Пересечение многогранника прямой | ||
| Алгоритм решения (рис. 8.6) 1. Через прямую проводим вспомогательную секущую плоскость: l Ì S . 2. Строим сечение многогранника плоскостью: DEF = Фмн ∩ S. 3. Определяем точки пересечения прямой с построенной фигурой сечения: M, N = l ∩D DEF. | 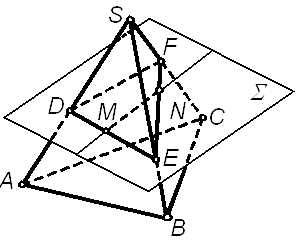
| |
| Рис. 8.6 | ||
| Задача. Найти точки пересечения прямой l с пирамидой SАВС (рис. 8.7). | ||
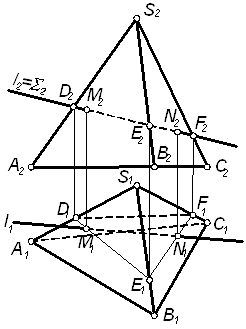
| Алгоритм решения 1. l Ì S Þ l2 = S2. 2. DEF = Фмн ∩ S ÞD2 = S2 ∩ A2S2 , D1 Î A1S1 E2 = S2 ∩ B2S2 , E1 Î B1S1 F2 = S2 ∩ С2S2 , F1 ÎC1S1. 3. M,N = l ∩Δ DEF Þ M1 = l1 ∩ D1E1, M2 Î l2 N1 = l1 ∩ F1E1, N2 Î l2. Видимость определяем по представлению. Грани АSB и BSC видимы на обеих проекциях, значит, видимы и точки M и N в них лежащие, и прилегающие к точкам участки прямой l. Невидимым является только участок прямой, лежащий внутри пирамиды. На П1 невидимым будет ребро АС пирамиды: скрещивающееся и конкурирующее с ним в видимости ребро SB расположено ближе к наблюдателю. | |
| Рис. 8.7 | ||
| 8.4. Взаимное пересечение многогранников | ||
| Линией пересечения двух многогранников является пространственная замкнутая ломаная, вершины которой – точки пересечения ребер одного многогранника с гранями второго и ребер второго с гранями первого, а сторонами – линии взаимного пересечения граней многогранников (рис. 8.8, 8.9). | ||

| 
| |
| Рис. 8.8 | Рис. 8.9 | |
| При взаимном пересечении двух многогранников могут встретиться два случая: врезки (неполного пересечения) и проницание. Врезкой называется случай, когда ни одна из поверхностей не пересекает другую полностью (рис. 8.8). Проницанием называется случай, когда одна из поверхностей полностью пересекается другой поверхностью (рис. 8.9). В случае врезки линия пересечения состоит из одной ломаной, а в случае проницания – из двух. Задача. Построить проекции линии пересечения двух многогранников (рис. 8.10). | ||

| ||
| Рис. 8.10 | ||
| Алгоритм решения | ||
1. Поскольку поверхность призматического отверстия полностью пересекает поверхность пирамиды (случай проницания), то линия пересечения (ЛП) состоит из двух пространственных замкнутых ломаных. Боковые грани призмы – фронтально-проецирующие, поэтому фронтальная проекция ЛП совпадает с фронтальной проекцией призматического отверстия, при этом проекции обоих фронтально конкурирующих контуров ЛП совпадают.
2. Находим вершины ЛП – точки пересечения ребер призмы с поверхностью пирамиды. Поскольку ребра призмы являются фронтально-проецирующими, то точки пересечения их с поверхностью пирамиды на П2 совпадают с вырожденными проекциями самих ребер: n2 =12=22, l2 = 32 = 42, l2 = 52 = 62. На П1 эти вершины находим методом вспомогательных секущих плоскостей (см. рис. 8.10):
- проводим плоскость Г (Г2 )через ребро n параллельно основанию пирамиды;
- строим пересечение k пирамиды этой плоскостью: на П2 – k2 , а на П1 проекция пересечения k1 будет квадратом, стороны которого параллельны сторонам основания, т.к. боковые грани пирамиды пересекаются параллельной плоскостью по параллельным прямым. Для построения этого сечения находим его вершину – точку 7 сначала на П2 – 72 = Г2 ∩ А2, а затем и на П1 по принадлежности ребру А пирамиды –71  А1;
- построив квадрат k1, по принадлежности ему находим проекции точек 1 и 2 на П1;
- по аналогичному алгоритму с помощью вспомогательной плоскости Г*(Г*2) находим горизонтальные проекции точек 3, 4, 5, 6. Профильные проекции найденных вершин находим по двум известным – по линиям святи через К0, или используя более простой и точный метод, употребляемый в инженерной практике. Выбирается базовая плоскость для отсчета нужных размеров вдоль оси y13. Если фигура имеет плоскость симметрии, то базовую плоскость проводят через нее. В нашем случае за такую плоскость принимаем фронтальную плоскость Ф, которая проходит через ось пирамиды, задавая ее вырожденными проекциями Ф1 и Ф3. Для построения профильной проекции какой-либо точки (например 1) замеряем расстояние от Ф1 до 11 (V) и откладываем его на П3 по горизонтальной линии связи от Ф3 вправо (для этого всегда нужно иметь в виду наличие К0, даже когда она не нанесена на чертеж) и получаем проекцию 13 . А1;
- построив квадрат k1, по принадлежности ему находим проекции точек 1 и 2 на П1;
- по аналогичному алгоритму с помощью вспомогательной плоскости Г*(Г*2) находим горизонтальные проекции точек 3, 4, 5, 6. Профильные проекции найденных вершин находим по двум известным – по линиям святи через К0, или используя более простой и точный метод, употребляемый в инженерной практике. Выбирается базовая плоскость для отсчета нужных размеров вдоль оси y13. Если фигура имеет плоскость симметрии, то базовую плоскость проводят через нее. В нашем случае за такую плоскость принимаем фронтальную плоскость Ф, которая проходит через ось пирамиды, задавая ее вырожденными проекциями Ф1 и Ф3. Для построения профильной проекции какой-либо точки (например 1) замеряем расстояние от Ф1 до 11 (V) и откладываем его на П3 по горизонтальной линии связи от Ф3 вправо (для этого всегда нужно иметь в виду наличие К0, даже когда она не нанесена на чертеж) и получаем проекцию 13 .
| ||
| 3. Находим вершины ломаной 9, 10, 11, 12, – точки пересечения ребер пирамиды B и D с поверхностью призмы. Находим сначала на П2, как результат пересечения проекций этих ребер пирамиды с вырожденными проекциями граней nm и ml призмы. Проекции этих вершин на П1 и П3 находим по принадлежности ребрам пирамиды сначала на П3, а затем и на П1 методом, описанным выше. 4. Соединяем найденные вершины отрезками прямых, руководствуясь правилом: соединять отрезками можно лишь вершины, которые лежат в одной грани призмы и одной грани пирамиды. Во избежание ошибок составляем последовательность соединения вершин: 1 – 5 – 11 – 3 – 9 – 1 и 2 – 6 – 12 – 4 – 10 – 2. 5. Определяем видимость ЛП по представлению. Видимыми будут звенья ЛП, которые являются линиями пересечения видимых на проекции граней призмы и пирамиды. На П1 видимы грани mn и nl призмы и части боковых граней пирамиды, расположенные выше призмы, потому находящиеся в них участки ЛП 3 – 1 – 5 – 2 – 7 – 4 будут видимы. Невидимыми на П1 являются звенья, расположенные в грани ml. На П3 видима грань mn призмы и лежащие в ней звенья ЛП 1–5–2. Все остальные участки ЛП или невидимы, или совпадают с вырожденной проекцией грани ml призмы. 6. Определяем видимость ЛП и ребер поверхностей по представлению. О видимости ЛП на фронтальной проекции уже говорилось выше: видимый и невидимый контуры ЛП совпадают, как и видимые и невидимые ребра пирамиды. При взгляде сверху (на П1) все звенья ЛП видимы, поскольку лежат на видимых боковых гранях пирамиды. Ребра пирамиды являются видимыми, кроме участков 91111 и 101121, вырезанных отверстием. Ребра призматического отверстия проходят внутри пирамиды и невидимы. На П3 видимыми будут звенья ЛП (9333113) и (10343123), которые лежат на видимых слева (см. П2 совместно со стрелкой – направлением взгляда на П3) гранях пирамиды AB и AD. Последние звенья ЛП лежат на невидимых слева гранях пирамиды ВС и СD и являются невидимыми, но поскольку часть пирамиды вырезана, то участки ЛП 1353 и 2363, которые не закрыты материалом пирамиды (ограниченным звеньями 9333113 и 10343123), который остался, будут видны. Видимость ребер поверхностей на П3 такая же, как на П1. | ||
Вопросы для самопроверки
- Какие элементы характеризуют многогранную поверхность?
- Каким образом многогранная поверхность задается на чертеже?
- Как можно определить, принадлежит ли точка многогранной поверхности?
- От чего зависит количество вершин плоской фигуры, которая образуется при пересечении многогранника с плоскостью?
- Сколько правильных многогранников вам известно? Какие фигуры образуют все грани правильного многогранника?
- Как называют пирамиду, основанием которой является правильный многоугольник, а вершина проецируется в центр основания?
- Как образуются вершины и стороны пространственной ломаной линии, которая является результатом пересечения двух многогранных поверхностей?
- При каком случае пересечения поверхностей (полное или частичное) пространственная замкнутая ломаная распадается на две отдельных ломаных линии?
| 9. КРИВЫЕ ЛИНИИ В начертательной геометрии кривую линию рассматривают как траекторию непрерывно движущейся точки. Кривые могут быть плоскими и пространственными. Кривые могут быть заданы алгебраической или трансцендентной функцией, или графически. Порядок кривых может быть определен степенью алгебраического уравнения; или графически по числу точек пересечения кривой с прямой линией (для плоских кривых); по числу точек пересечения кривой с плоскостью (для пространственных кривых). В начертательной геометрии кривые линии задаются на чертеже их проекциями. | ||||
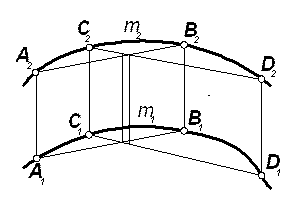 Рис. 9.1 Рис. 9.1
| Чтобы определить, какая – плоская или пространственная кривая задана на чертеже, нужно провести две секущих, одноименные проекции которых бы пересекались, и определить их взаимное положение: если они пересекаются, то кривая плоская, если скрещиваются – пространственная. На рис. 9.1 изображена пространственная кривая, так как секущие АВ и CD скрещивающиеся: точки пересечения одноименных проекций не лежат на одной линии связи. | |||
| 9.1. Плоские кривые. Касательные и нормали Направление движения точки в каждом её положении определяется касательной прямой t в данной точке А кривой линии (рис. 9.2). | ||||

| Касательной прямой t в точке A кривой называется предельное положение секущей AA*, когда A* оставаясь на кривой m, стремится к точке A. Нормалью n к кривой в точке A называется прямая, лежащая в плоскости кривой m и перпендикулярная к касательной t в этой точке. Кривая называется гладкой, если она во всех своих точках имеет непрерывно изменяющуюся касательную, которая в каждой точке кривой единственная. На кривых различают особые точки (рис. 9.3): | |||
| Рис. 9.2 | ||||

| ||||
| Рис. 9.3 | ||||
| А – точка возврата 1-го рода, В – точка возврата 2-города, С – точка перегиба, D – кратная точка, Е – точка излома. 9.2. Основные свойства проекций плоских кривых линий 1. Порядок плоской алгебраической кривой при параллельном проецировании не изменяется. 2. Бесконечно удаленные точки кривой проецируются в бесконечно удаленные точки её проекций. 3. Касательная к кривой проецируется в касательную к её проекции. 4. Точки пересечения плоских кривых проецируются в точки пересечения их проекций | ||||
9.3 Кривые второго порядка
Наиболее распространенные в разных областях техники кривые второго порядка: эллипс, гипербола, парабола, окружность.
Эллипсом називается множество точек плоскости, сумма расстояний от каждой из которых к двум данным точкам (фокусов) является величиной постоянной, большей чем расстояние между фокусами и равняется 2а. Расстояние между фокусами 2с называется фокусным (рис. 9.4а).
Уравнение эллипса:
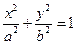 , где , где 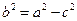 Гиперболой называются плоскости, разность расстояний которых к двум данным точкам (фокусам) – величина постоянная, равная 2а. Гипербола имеет две оси (х – действительная, у – воображаемая) и две асимптоты m, n – прямые, на которых лежат несобственные точки гиперболы (рис. 9.4б). Уравнение гиперболы:
Гиперболой называются плоскости, разность расстояний которых к двум данным точкам (фокусам) – величина постоянная, равная 2а. Гипербола имеет две оси (х – действительная, у – воображаемая) и две асимптоты m, n – прямые, на которых лежат несобственные точки гиперболы (рис. 9.4б). Уравнение гиперболы:
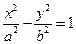 , где , где 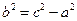 Парабола – это множество точек на плоскости, равноудаленных от заданой точки (фокуса) и данной прямой (директрисы). На рис. 9.4в показано построение параболы.
Уравнение параболы в прямоугольных декартовых координатах:
Парабола – это множество точек на плоскости, равноудаленных от заданой точки (фокуса) и данной прямой (директрисы). На рис. 9.4в показано построение параболы.
Уравнение параболы в прямоугольных декартовых координатах: 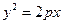 . .
| ||||
| ||||
| Рис. 9.4 | ||||
| 9.3.1 Проецирование окружности В зависимости от положения плоскости окружности относительно плоскостей проекций она может проецироваться в виде окружности, эллипса или прямолинейного отрезка. Если плоскость окружности параллельна какой-либо плоскости проекций, то она проецируется в неё в натуральную величину. | ||||
| Если плоскость окружности занимает проецирующее положение (рис. 9.5), то на плоскость проекций, перпендикулярную плоскости Σ, окружность проецируется в виде отрезка А1В1, величина которого равна диаметру окружности АВ. | ||||
| В плоскости проекций, к которым плоскость S наклонена, окружность проецируется в виде эллипса. При этом: - центром эллипса О2 является проекция центра О окружности; - большой осью эллипса будет проекция диаметра окружности параллельного плоскости проекций и равняется диаметру окружности (С2D2 = CD); - малой осью эллипса будет проекция того диаметра окружности, который проецируется с наибольшим искажением в рассматриваемую плоскость проекций. На рис. 9.4 это диаметр АВ, который лежит на линии наибольшего наклона плоскости S к П2. | ||||
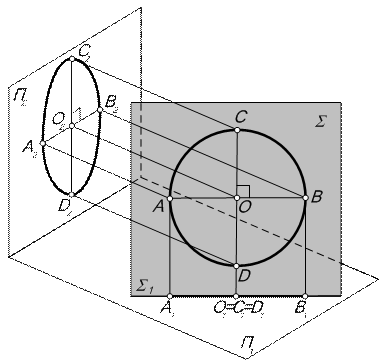 Рис. 9.5
Рис. 9.5
| ||||
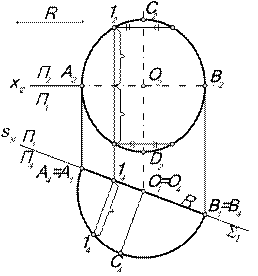 Рис. 9.6
Рис. 9.6
| Задача. Построить проекции окружности радиуса R, расположенной в горизонтально проецирующей плоскости S (рис. 9.6). Алгоритм решения 1. Так как плоскость S окружности горизонтально проецирующая, то в П1 окружность проецируется в виде отрезка на проекции S1 плоскости, длина которого равна 2R, а на П2 – в эллипс (см. выше рис. 9.4), оси которого – проекции двух взаимно перпендикулярных диаметров окружности: большая ось – проекция диаметра CD параллельного плоскости проекций П2 и проецируется на П2 в натуральную величину 2R, малая ось – проекция диаметра АВ, расположенного на линии наибольшего наклона к П2, в этом случае это горизонталь, фронтальная проекция которой параллельна оси x12). | |||
| 2. Для построения промежуточных точек эллипса П2 заменяем на П4, располагая последнюю параллельно плоскости S окружности: П2 → П4 || S, П1 / П2 (x12)→П1 / П4 (s14 || S1). В системе П1 / П4 нам известны обе проекции окружности и можно взять любую точку на окружности, например 14, а затем построить её проекции в П1 и П2 по алгоритму построения проекций точек при замене плоскостей проекций. Построив 12, можно воспользоваться свойством симметрии эллипса и построить ещё три точки, симметричные 12 относительно осей А2В2 и C2D2. Соединив лекалом построенные на П2 точки, получим эллипс – фронтальную проекцию окружности. | ||||
| 9.4 Пространственные кривые линии Пространственные кривые линии – это линии, точки которых не принадлежат одной плоскости.В инженерной практике чаще всего встречаются две пространственные кривые: цилиндрическая винтовая линия, или гелиса, и коническая винтовая линия.В отличие от плоских кривых, пространственные задаются двумя проекциями | ||||
| 9.4.1 Цилиндрическая винтовая линия | ||||
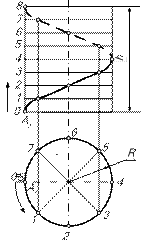 Рис. 9.7
Рис. 9.7
| Цилиндрическая винтовая линия или гелиса образуется при равномерном движении точки по образующей, которая в свою очередь, равномерно вращается вокруг оси. Винтовая линия задаётся радиусом основания R цилиндра и шагом h – величиной перемещения точки по образующей при повороте её вокруг оси на 3600 (рис. 9.7). Чтобы построить проекции винтовой линии, окружность и шаг разбиваются на n равных частей (например, на 8, как на рис. 9.7). | |||
Величину 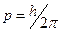 называют параметром винтовой линии . Поворот точки на 1/n части окружности соответствует её перемещению вдоль оси цилиндра на 1/n части шага: если точка А переместится из исходного положения (0) в положение 1, то проекция А1 окажется в точке 1 окружности, а её фронтальная проекция А2 – на горизонтали под тем же номером. называют параметром винтовой линии . Поворот точки на 1/n части окружности соответствует её перемещению вдоль оси цилиндра на 1/n части шага: если точка А переместится из исходного положения (0) в положение 1, то проекция А1 окажется в точке 1 окружности, а её фронтальная проекция А2 – на горизонтали под тем же номером.
| ||||
| Последовательно перемещая горизонтальную проекцию точки А1 в следующие положения, строим соответствующие фронтальные её проекции, соединив которые плавной кривой получаем фронтальную проекцию винтовой линии – синусоиду. На прямоугольнике развертки цилиндра гелиса изображается его диагональю. Гелиса является кратчайшей линией на цилиндре между двумя его точками. Рассматривают правую и левую винтовые линии. Если при вращении точки вокруг оси цилиндра по часовой стрелке эта точка удаляется от наблюдателя, то такая винтовая линия называется правой. | ||||
Вопросы для самопроверки
- Как определить порядок алгебраической кривой линии?
- Назовите особые точки кривой.
- Какие свойства плоских кривых не изменяются при параллельном проецировании?
- На какие линии может ортогонально проецироваться окружность?
- Как образуется цилиндрическая винтовая линия?
- Какие параметры надо задать для определения формы и положения винтовой линии?
| 10. КРИВЫЕ ПОВЕРХНОСТИ Для задания и образования поверхностей используются следующие способы: - аналитический - каркасный - кинематический. В начертательной геометрии пользуются кинематическим способом задания поверхностей и рассматривают поверхность как образованную непрерывным перемещением некоей линии в пространстве по определенному закону. Линия, которая формирует поверхность при перемещении в пространстве, называется образующей. Закон движения образующей определяется направляющими элементами и положением образующей относительно этих элементов в любой момент движения. Образующая может сохранять свою форму при изменении положения, или непрерывно изменять и форму, и положение в пространстве. Определитель поверхности – совокупность всех условий, определяющих поверхность. Определитель поверхности состоит из двух частей – геометрической и алгоритмической (или кинематического закона): - геометрическая часть определителя – совокупность геометрических элементов (образующая, направляющие элементы), которые определяют поверхность; - алгоритмическая часть – закон, который позволяет в любой момент движения образующей задавать ее положение и форму. | |||||||
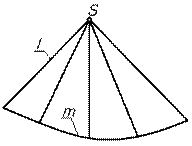 Рис. 10.1
Рис. 10.1
| Например, геометрической частью определителя конической поверхности, изображенной на рис. 10.1, является совокупность образующей l, и направляющих элементов m и вершины S. Алгоритмическая часть определителя устанавливает взаимное положение этих геометрических элементов в процессе формирования поверхности: l ∩ m, S Î l. | ||||||
| 10.1. Очерк поверхности | |||||||
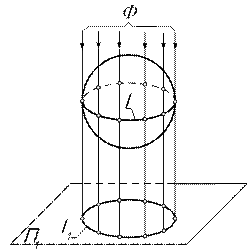 Рис. 10.2
Рис. 10.2
| Графическое задание поверхности проекциями элементов ее определителя обеспечивает обратимость чертежа, но не обеспечивает его наглядности. Для придания наглядности изображению поверхности строят очерки поверхности на плоскостях проекций. Для этого проводят проецирующие лучи, касающиеся поверхности, например, сферы (рис. 10.2). Проецирующие лучи образуют некоторую поверхность Ф, касающуюся заданной поверхности по линии l, которая называется контурной. Очерком поверхности является линия пересечения проецирующей поверхности Ф с плоскостью проекций, то есть очерк поверхности является проекцией l1 контурной линии l на данную плоскость проекций. | ||||||
| Очерк поверхности является границей видимости частей поверхности на данной плоскости проекций: точки, расположенные на сфере выше линии l, будут видимы при взгляде сверху, а точки ниже линии l – не видимы. | |||||||
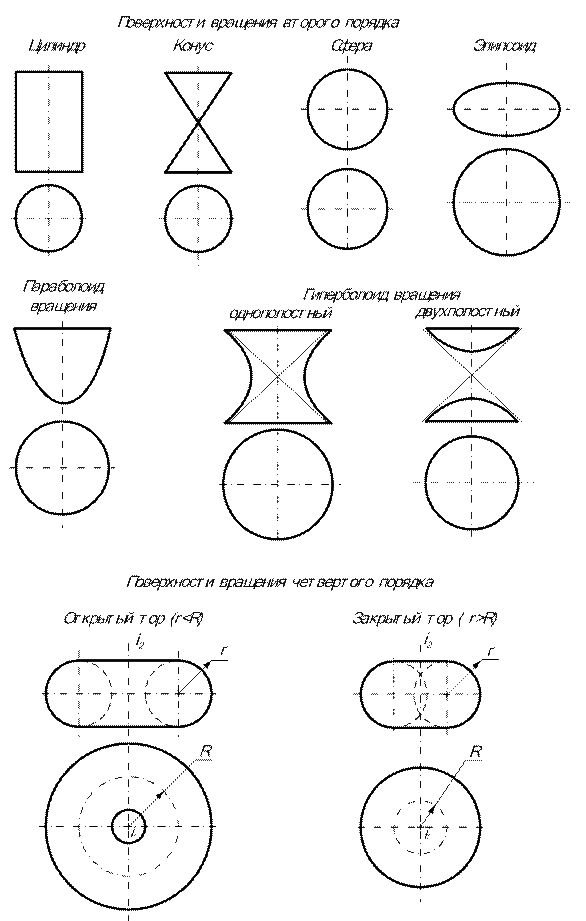
| 10.2. Поверхности вращения Поверхностью вращения называется поверхность, образованная при вращении линии (образующей) вокруг неподвижной оси. В инженерной практике поверхности вра-щения задаются, как правило, своими очерками (рис. 10.3, 10.4). На рис. 10.4 показаны поверхности вращения, наиболее часто встречающиеся в инженерной практике. 10.2.1. Основные линии поверхности вращения Параллель – сечение поверхности вращения плоскостью, перпендикулярной оси вращения. Представляет собой окружность, которая на плоскость проекций, перпендикулярную оси, проецируется в натуральную величину, а в плоскость, параллельную оси, – в виде отрезка, перпендикулярного проекции оси и равного диаметру параллели. Наибольшая из близлежащих параллелей называться экватором, наименьшая – горлом. Меридиан – пересечение поверхности вращения плоскостью, проходящей через ось вращения. Меридиан, расположенный в плоскости, параллельной плоскости проекций, называется главным меридианом и определяет очерк поверхности в этой плоскости. С помощью этих линий строятся точки, принадлежащие поверхности. При этом используется признак принадлежности точки поверхности: Точка принадлежит поверхности, если она лежит на линии этой поверхности. | |||||||
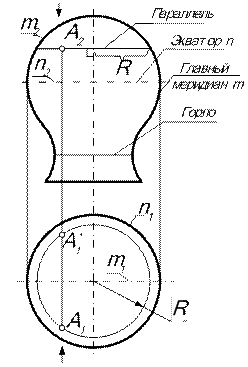 Рис. 10.3
Рис. 10.3
| |||||||
| Например, с помощью параллели радиуса R на поверхности построены проекции точки А: через заданную фронтальную проекцию А2 проведена проекция параллели и построена ее горизонтальная проекция, по принадлежности которой найдена горизонтальная проекция А1. При этом заданному положению А2 отвечают два положения горизонтальной проекции точки: А1, если точка А видима на П2, и А1*, если она на П2 невидима. | |||||||
| |||||||
| Рис 10.4 | |||||||
| 10.3. Пересечение криволинейной поверхности плоскостью Поверхности вращения второго порядка пересекаются плоскостью по кривым второго порядка. 10.3.1. Сферические сечения При пересечении сферы плоскостью всегда получается окружность. Если секущая плоскость расположена под углом к плоскости проекций, то проекцией окружности является эллипс. При пересечении сферы плоскостью S в сечении получается окружность, центр которой расположен на прямой n, проходящей через центр сферы и перпендикуляр- | |||||||
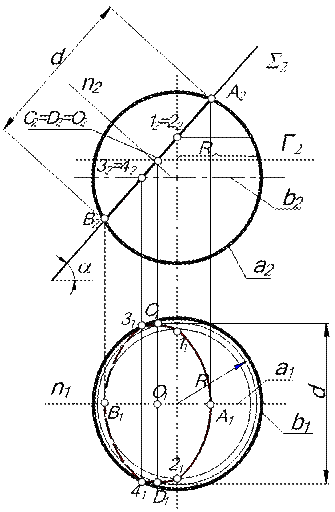 Рис. 10.5 Рис. 10.5
| ной плоскости окружности (сечению) О = S ∩ n (О2 = n ^ S); О1 Î n1 (смотри рис. 10.5). Окружность сечения на П2 проецируется в отрезок. На П1 – в эллипс. Диаметры, которые лежит на прямых уровня плоскости S, проецируется в большую и малую оси эллипса. Т.к. [СD] ^ П2 Þ [СD] || П1. [С1D1] = d сферы. [С1D1] – большая ось эллипса. Малая ось перпендикулярна большой и является проекцией диаметра [АВ], расположенного параллельно П2. |А1В1| = |АВ|cosa. Горизонтальные проекции С1 и D1 точек С и D можно также построить по принадлежности их сфере (с помощью вспомогательной секущей плоскости Г). При пересечении сферы плоскостью Г в сечении получается окружность радиусом R. Поскольку Г || П1, то окружность в горизонтальную плоскость проекций проецируется в натуральную величину и С1, D1 находим по принадлежности этой окружности. | ||||||
10.3.2. Цилиндрические сечения
Вид цилиндрического сечения (рис. 10.6) зависит от положения секущей плоскости относительно оси цилиндра:
1. Плоскость перпендикулярна оси цилиндра: в сечении – окружность с центром О на оси и радиусом, равным радиусу цилиндра Г ^ i, Г ∩ Фцил = окружность n (О, R);
| |||||||
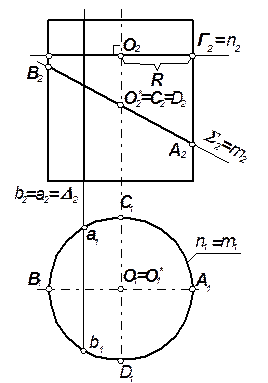 Рис. 10.6
Рис. 10.6
| Цилиндрическая поверхность является проецирующей к плоскости проекций, перпендикулярной к оси цилиндра, потому в эту плоскость (на рис. 10.4 в П1) сечения цилиндра проецируются на окружность – вырожденную проекцию (очерк) поверхности. | ||||||
| 10.3.3. Конические сечения Вид конического сечения зависит от следующих факторов (рис. 10.7): | |||||||
1. Положение секущей плоскости относительно вершины конуса:
- если плоскость проходит через вершину конуса (D  S)– в сечении две пересекающиеся прямые (образующие конуса);
- если плоскость не проходит через вершину – в сечении кривые другого порядка.
2. Угол b между секущей плоскостью и осью конуса:
- если угол – 90° ( Г ^ i), то в сечении окружность (О, r) (параллель конуса);
- если угол не равняется 90° – в сечении эллипс, парабола или гипербола.
3. Соотношение между углом b наклона секущей плоскости к оси конуса и углом a между осью конуса и его образующей:
а) b > a, S ∩ Фкон = эллипс; большая ось эллипса – АВ, малая – CD; S)– в сечении две пересекающиеся прямые (образующие конуса);
- если плоскость не проходит через вершину – в сечении кривые другого порядка.
2. Угол b между секущей плоскостью и осью конуса:
- если угол – 90° ( Г ^ i), то в сечении окружность (О, r) (параллель конуса);
- если угол не равняется 90° – в сечении эллипс, парабола или гипербола.
3. Соотношение между углом b наклона секущей плоскости к оси конуса и углом a между осью конуса и его образующей:
а) b > a, S ∩ Фкон = эллипс; большая ось эллипса – АВ, малая – CD;
| 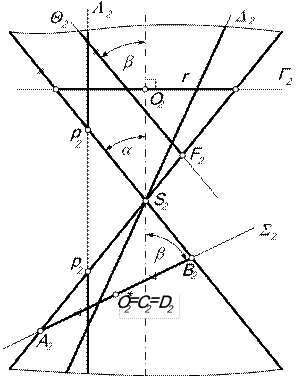 Рис. 10.7
Рис. 10.7
| ||||||
| центр эллипса О* не лежит на оси конуса, а находится делением отрезка АВ пополам (А2О*2 = В2О*2). б) b = a, Q ∩ Фкон = парабола з вершиной F; в) b < a, L ∩ Фкон = гипербола з вершинами в точках Р. | |||||||
| 10.4. Построение сечения поверхности вращения плоскостью Чтобы построить сечение, необходимо найти достаточное количество точек, ему принадлежащих, и в первую очередь должны быть найдены особые точки сечения, к которым относятся: 1. Геометрически особые точки сечения (вершины, центры, точки на концах осей эллипса и тому подобное) 2. Граничные точки видимости (опорные точки) – точки пересечения очерковых линий поверхности с секущей плоскостью. Задача. Построить проекции и натуральную величину пересечения конуса плоскостью ( (рис. 10.8). Алгоритм решения 1. Определяем вид сечения и его проекций. Поскольку S не проходит через вершину конуса S и угол b наклона ее к оси конуса больше угла a между осью и образующей, то в сечении – эллипс + отрезок, результат пересечения секущей плоскости с плоскостью основания. Т.к. секущая плоскость – фронтально проецирующая, то на П2 сечение проецируется в виде отрезка, который лежит на вырожденной проекции S2 секущей плоскости внутри очерка конуса. | |||||||
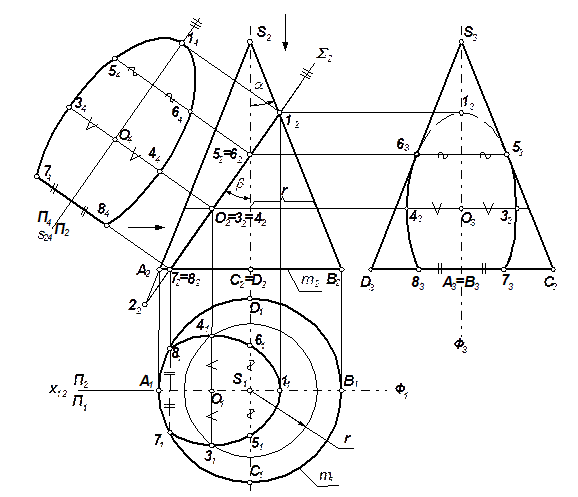 Рис. 10.8
Рис. 10.8
| |||||||
| Находим особые точки сечения: центр эллипса, точки на концах его осей, граничные точки видимости. Чтобы построить эти точки, необходимо обозначить очерковые образующие конуса: A2S2, B2S2 на П2, C3S3, D3S3 на П3 и найти их проекции на остальных плоскостях. Сначала находим проекции особых точек сечения на его известной фронтальной проекции. Продлив вырожденную проекцию S2 секущей плоскости до пересечения с продолжением очерковой A2S2, находим точку 22 – фронтальную проекцию точки, которая | |||||||
12
Дата добавления: 2016-04-11; просмотров: 2331;

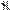 i, S ∩ Фцил = эллипс (О*, AB, CD = R).
i, S ∩ Фцил = эллипс (О*, AB, CD = R).