1 страница. Вопросы для самопроверки Какая проекция фронтали на двухкартинном чертеже параллельна оси проекций?

Вопросы для самопроверки

1. Какая проекция фронтали на двухкартинном чертеже параллельна оси проекций?
2. В какую плоскость проекций отрезок горизонтальной прямой проецируется на конгруэнтный отрезок?
3. Какую плоскость проекций пересекает фронтальная прямая?
4. С какой плоскости проекций необходимо начинать построение произвольной горизонтальной прямой уровня?
5. Какой плоскости проекций параллельна горизонтально-проецирующая прямая?

4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Прямые в пространстве могут располагаться параллельно друг другу, пересекаться или скрещиваться. Прямые параллельны, если они принадлежат одной плоскости и не имеют общей точки. Прямые пересекаются, если они принадлежат одной плоскости и имеют одну общую точку. Прямые скрещиваются, если они не параллельны и не пересекаются.
Если прямые параллельны, то их одноименные проекции параллельны между собой или совпадают (рис.4.1).
Рис. 4.1	Рис. 4.2
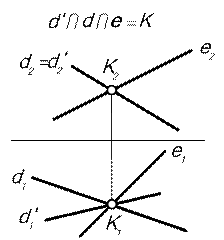
Если прямые пересекаются, то их одноименные проекции пересекаются (или совпадают), при этом точки пересечения проекций всегда лежат на одной линии проекционной связи (рис. 4.2).
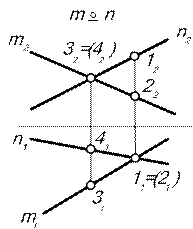
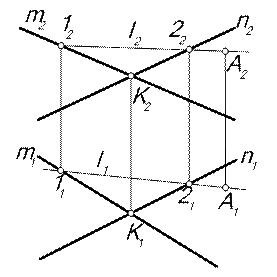
	Если прямые скрещивающиеся, то точки пересечения одноименных проекций не лежат на одной линии связи. Точки пересечения проекций – совпадающие проекции конкурирующих точек, которые принадлежат скрещивающимся прямым (рис. 4.3).
Рис. 4.3

Вопросы для самопроверки

1. Достаточно ли двух проекций прямых для определения их параллельности?
2. Какое условие необходимо для определения параллельности профильных прямых в пространстве?
3. При каком взаимном положении прямые лежат в одной плоскости?
4. Могут ли взаимно перпендикулярные прямые быть скрещивающимися?
5. Сколько общих точек могут иметь пересекающиеся прямые?

	5. КОМПЛЕКСНЫЙ ЧЕРТЕЖ ПЛОСКОСТИ
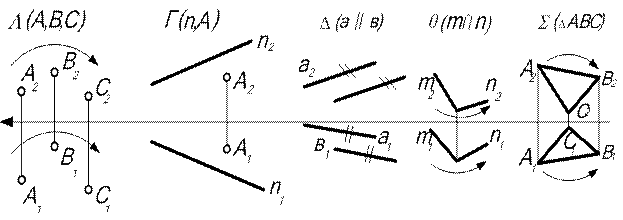
	Плоскость считается заданной на чертеже, если: - возможно построить проекции любой точки, принадлежащей плоскости; - возможно определить, принадлежит ли данной плоскости заданная на чертеже точка. В общем случае плоскость задается на чертеже проекциями своего определителя, под которым понимается совокупность элементов, которые однозначно задают плоскость в пространстве (рис. 5.1): три точки, не лежащие на одной прямой; прямая и точка вне прямой; две пересекающиеся прямые; две параллельные прямые; плоская фигура.
	Рис. 5.1
	5.1. Положение плоскости относительно плоскостей проекций
	5.1.1. Плоскость общего положения Определение: плоскость, наклоненная ко всем плоскостям проекций (рис. 5.2). Признак: ни на одну из плоскостей проекций определитель плоскости не проецируются на прямую (см. рис. 5.1).
	Свойства чертежа: фигура в плоскости общего положения, углы наклона ее к плоскости проекций ни на одну плоскостям проекций не проецируются в натуральную величину. Восходящей называется плоскость, высота точек которой возрастает по мере удаления от наблюдателя, а нисходящей – плоскость, высота точек которой уменьшается по мере удаления от наблюдателя. Признак: у восходящей плоскости обход проекций точек на обеих плоскостях проекций одинаковый (плоскость L и q на рис. 5.1), у нисходящей – противоположный (плоскость S на рис. 5.1). У восходящей плоскости, видна на П1 и П2 одна и та же сторона, у нисходящей – разные стороны.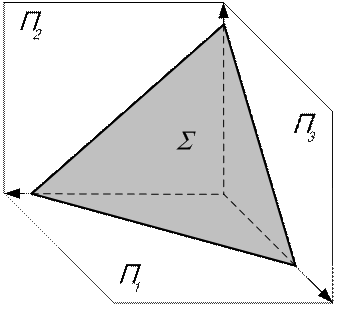
	Рис. 5.2
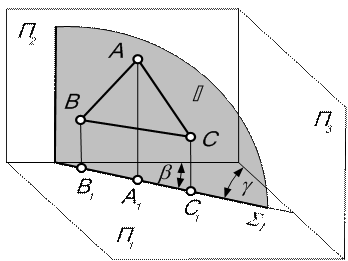
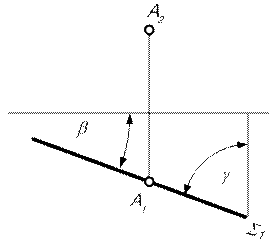
5.1.2. Проецирующая плоскость
Определение: плоскость, перпендикулярная какой-либо плоскости проекций (рис. 5.3). Признак: проекция плоскости на перпендикулярную плоскость проекций – прямая (вырожденная проекция плоскости), наклоненная к осям проекций (S на рис. 5.3, 5.4). На комплексном чертеже проецирующие плоскости задаются, как правило, своими вырожденными проекциями (см. рис. 5.4). Свойства чертежа:вырожденная проекция обладает собирательным свойством: проекция фигуры, расположенной в плоскости, в перпендикулярную плоскость проекций располагается на вырожденной проекции проецирующей плоскости. Углы наклона вырожденной проекции к осям проекций равны углам наклона плоскости к соответствующим плоскостям проекций.
Рис. 5.3	Рис. 5.4
В зависимости от плоскости проекций, к которой перпендикулярна плоскость, проецирующие плоскости называются горизонтально, фронтально или профильно-проецирующими.
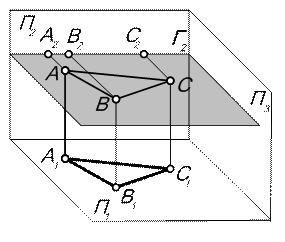
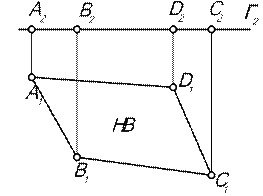
5.1.3. Плоскость уровня
Определение: плоскость, параллельная какой-либо плоскости проекций (рис. 5.5). Признак: проекция плоскости на перпендикулярные плоскости проекций – прямая (вырожденная проекция) Г2, параллельны соответствующим осям проекций (рис. 5.6). Свойства чертежа: фигура в плоскости уровня в параллельную плоскость проекций проецируется в натуральную величину.
Рис. 5.5	Рис. 5.6
5.2. Принадлежность прямой и точки плоскости
Прямая принадлежит плоскости: а) если прямая проходит через две точки, принадлежащие плоскости; б) если прямая проходит через точку плоскости и параллельна прямой, лежащей в плоскости. Точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости.
Задача. Построить недостающую проекцию точки А, принадлежащей плоскости S (m ∩ n), (рис.5.7).
	Алгоритм решения 1. Через известную горизонтальную проекцию точки А (А1) проводим проекцию произвольной прямой l так, чтобы она пересекала прямые m и n, задающие плоскость S: А1 Î l1 2. Находим проекции точек 1 и 2 пересечения прямой l с прямыми m и n: 11 = l1 ∩ m1, 21 = l1 ∩ n1, 12 Î m2 , 22 Î n2 3. Соединив 12 и 22, получаем фронтальную проекцию прямой l, по принадлежности которой и находим фронтальную проекцию точки А: А2 Î l2.
Рис. 5.7
5.3. Прямые особого положения в плоскости
5.3.1. Прямая уровня плоскости
Определение: прямая, принадлежащая плоскости и параллельная какой-либо плоскости проекций.
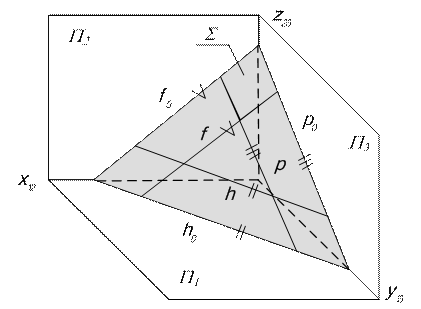Рис 5.8
Линии уровня плоскости по направлению параллельны соответствующим линиям пересечения данной плоскости S с плоскостями проекций (рис. 5.8): линия h0 –горизонталь, расположенная в горизонтальной плоскости проекций, линия f0 – фронталь, расположенная во фронтальной плоскости проекций, линия p0 –профильная прямая, расположенная в профильной плоскости проекций.
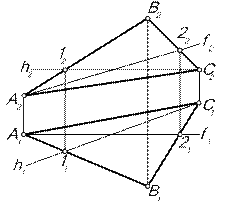
Задача. В плоскости q (D АВС) провести произвольные горизонталь и фронталь (рис. 5.9).
Рис. 5.9
Алгоритм решения 1. Т.к. требуется построить произвольные горизонталь и фронталь, то для удобства построений проведем их соответственно через вершины С и А треугольника. 2. Сначала проводим те проекции прямых, направление которых известны – фронтальную проекцию горизонтали h2 и горизонтальную фронтали f1: C2 Î h2 || X12 , А1 Î f1 || X12 . 3. Недостающие проекции прямых, находим по принадлежности их плоскости треугольника АВС, а именно по двум точкам, ей принадлежащим. Для этого находим точки 1 и 2 пересечения горизонтали и фронтали со сторонами АВ и ВС соответственно и соединяем их с одноименными проекциями А и С.
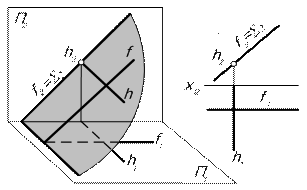
Рис. 5.10
В проецирующей плоскости прямая уровня, параллельная неперпендикулярной плоскости проекций – проецирующая прямая (рис. 5.10).

Вопросы для самопроверки

1. Какие вы знаете способы задания плоскости на комплексном чертеже?
2. Какие плоскости называются плоскостями уровня? Свойства этих плоскостей?
3. Какие плоскости называются проецирующими? Какие свойства этих плоскостей?
4. Сформулируйте условия принадлежности прямой плоскости.
5. Какие прямые называются горизонталями плоскости?
6. Какие прямые называются фронталями плоскости?

6. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ 6.1. Параллельность прямой и плоскости Определение: прямая и плоскость называются параллельными, если они не имеют общей точки. Признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой, которая лежит в плоскости.
Задача. Через точку М провести прямую l, параллельную плоскости D (a || b) и П1 (рис. 6.1).
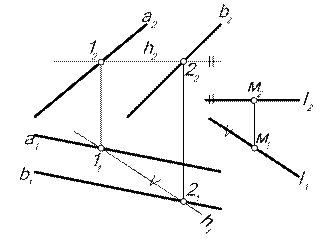Рис. 6.1	Алгоритм решения 1. Т.к. искомая прямая l должна быть параллельна П1, в плоскости D (a || b) проводим произвольную горизонталь h: сначала h2 || x12, а затем h1 по точкам 1 и 2: 1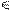1 h1 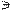21 2. Через проекции точки М проводим l2 || h2 и l1 || h1. Задача решена: прямая l || D (a || b), т.к. она параллельна h, лежащей в плоскости, и l || П1, т.к. l2 || x12.
6.2. Параллельность плоскостей Определение: плоскости называются параллельными, если не имеют общей точки. Признак: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
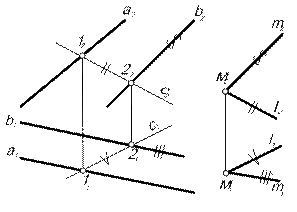Рис 6.2	Задача. Через точку М провести плоскость S, параллельную плоскости D (a || b) (рис. 6.2). Алгоритм решения 1. В заданной плоскости нет пересекающихся прямых, поэтому проводим в ней дополнительную прямую с , пересекающую прямые, задающие плоскость D (a || b). 2. Искомую плоскость S задаём двумя пересекающимися прямыми m || a и l || c, проведенными через точку М.
6.3. Пересечение прямой с плоскостью
Задача. Построить точку пересечения K прямой l с проецирующей плоскостью S.
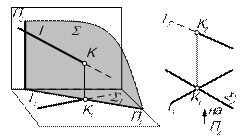Рис. 6.3
Алгоритм решения 1. Точка K общая для прямой и плоскости. Из условия принадлежности её плоскости S горизонтальная проекция К1 должна располагаться на вырожденной проекции плоскости S1. Из условия принадлежности её прямой l проекции точки должны лежать на проекциях прямой. Следовательно, К1 лежит в точке пересечения S1 и l1: l1 Î К1 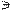S1 .Фронтальная проекция К2 находится по принадлежности прямой l: К2 Î l2. 2. Видимость прямой на П2 определяем «по представлению»: рассматриваем горизонтальную проекцию совместно с направлением взгляда наблюдателя на П2 и видим, что при взгляде на П2 часть прямой правее точки К располагается за плоскостью S и поэтому является невидимой   Задача. Построить линию пересечения двух плоскостей, одна из которых проецирующая (рис. 6.4).
Алгоритм решения 1. Линия пересечения m принадлежит фронтально-проецирующей плоскости, следовательно, фронтальная проекция линии совпадает с вырожденной проекцией плоскости: m2 = S2 .
Рис. 6.4	2. Линия пересечения m принадлежит плоскости треугольника АВС, следовательно, она пересекает стороны треугольника АВ и АС в точках 1 и 2. Построив горизонтальные проекции этих точек по принадлежности сторонам треугольника и соединив их, получаем горизонтальную проекцию искомой линии пересечения m1 . 3. Видимость треугольника на П1 определяем так же , как и в предыдущей задаче, «по представлению»: рассматриваем фронтальную проекцию совместно с направлением взгляда наблюдателя на П1 и видим, что при взгляде сверху часть треугольника (А12) располагается ниже плоскости S и является невидимой

Вопросы для самопроверки

1. Фронтальная плоскость пересекает горизонтально-проецирующую плоскость. Какая прямая является результатом пересечения?

2. Как определить взаимное положение прямой и плоскости заданных на чертеже?

3. Что является результатом пересечения двух плоскостей, прямой и плоскости?

4. Горизонтальная проекция прямой параллельна вырожденной проекции горизонтально - проецирующей плоскости. Какое положение занимает прямая?

5. Результатом пересечения двух горизонтально-проецирующих плоскостей является прямая. Какое положение занимает прямая согласно плоскостей проекций

7. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА Цель преобразования – упростить чертеж, расположив заданные геометрические фигуры в более удобное для решения задачи частное положение. Методы преобразования чертежа используют для решения метрических и позиционных задач. Все они основаны на двух принципах: изменение взаимного положения объекта и плоскостей проекций; изменение направления проецирования. Основными задачами преобразований являются: 1. Прямую общего положения сделать прямой уровня. 2. Прямую общего положения сделать проецирующей прямой. 3. Плоскость общего положения сделать проецирующей. 4. Плоскость общего положения сделать плоскостью уровня. Одним из таких преобразований является способ замены плоскости проекций или построение проекции фигуры в дополнительную плоскость проекций. 7.1. Замена плоскостей проекций При этом способе преобразования чертежа положение фигуры в пространстве не изменяется, а заменяют одну из основных плоскостей проекций, проводя новую – дополнительную – плоскость проекций так, как это удобно для решения задачи. При этом новая плоскость должна быть перпендикулярной незаменяемой плоскости проекций. Рассмотрим этот способ на простом примере, когда фигурой в пространстве является точка. Допустим, в системе плоскостей проекций П1 / П2, где расположена точка А (рис. 7.1), решение задачи затруднено или вообще невозможно. Поэтому плоскость П2 заменяется на новую плоскость П4, которую располагают так, чтобы решение было облегчено. В новой системе плоскостей П1 / П4 с новой осью проекций s14 необходимо построить проекцию точки А4. По методу ортогонального проецирования из точки А опускается перпендикуляр на П4, а для нахождения точки его пересечения с П4 (проекции А4) через А1 проводится ломаная А1А14А4, оба звена которой перпендикулярны оси системы s14.
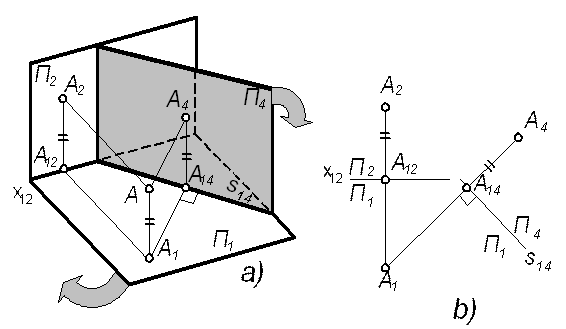Рис. 7.1
При переходе к новой системе плоскостей проекций остаются неизменными: - одна из плоскостей проекций и проекция фигуры в ней (в нашем случае П1 и А1), расстояние от фигуры до незаменяемой плоскости проекций (АА1), которое проецируется в натуральную величину как в замененную, так и новую плоскости проекций (АА1 = А2А12 = А4А14).
Для превращения пространственной конструкции (рис. 7.1а) в плоское изображение (чертеж) плоскость П1 вращением вокруг оси x12 совмещается с П2, а новая плоскость П4 вращается вокруг оси s14 до совмещения с П1. При этом ломаная А1А14А4 превращается в линию связи, перпендикулярную оси s14 (рис. 7.1б).
Таким образом построение проекции точки в дополнительную плоскость формализируется следующим алгоритмом: 1. В избранной системе двух плоскостей проекций одну из плоскостей оставляют неизменной. Выбор такой плоскости зависит от положения объекта и условия задачи: в рассмотренном примере (рис. 7.1) П1 – const, проекция А1 – const, удаление точки А от горизонтальной плоскости (высота) hA – const. 2. Вместо второй плоскости проекций применяют дополнительную плоскость проекций, которую располагают так, как нужно для решения задачи ( в рассмотренном примере П2 → П4 ^ П1). Таким образом, старая система плоскостей преобразована в новую систему, при чем как линией пересечения старых плоскостей была ось х12, так линией пересечения плоскостей в новой системе является ось s14: П1 / П2 (х12)→ П1 / П4 (s14). На чертеже новая система плоскостей моделируется изображениям новой оси, которую проводят рядом с имеющимся изображением. Таким образом заменяемыми являются плоскость П2 → П4, проекция А2 → А4, ось х12 → ось s14. 3. Строим проекцию точки в дополнительную плоскость: - Через незаменяемую проекцию точки (в данном случае А1) проводят линию связи, пер­пендикулярную новой оси проекций. - На новой линии связи от точки пересечения ее с новой осью откладывают отрезок, равный расстоянию между замененной проекцией точки и замененной осью (в рассмотренном примере расстояние между А2 и х12: |А2А12| = |А14А4| = hA ).
Задача. Прямую общего положения, заданную отрезком АВ, сделать прямой уровня (рис. 7.2). Чтобы прямую общего положения сделать прямой уровня, достаточно заменить одну из основных плоскостей проекций, проведя новую плоскость параллельно заданной прямой и перпендикулярно второй плоскости проекций.
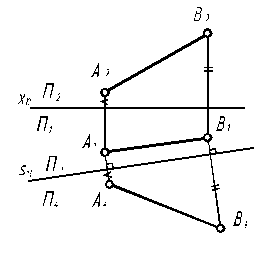
	В данном случае заменить можно любую плоскость, потому что это не отразится на результате. Если бы в условии задачи необходимо было определить угол наклона к одной из плоскостей проекций, выбор незаменяемой плоскости был бы однозначным. Алгоритм решения 1. П1 – const П2 → П4 || [AB] П1 / П2 (х12)→ П1 / П4 (s14 || [A1B1]) 2. Строим проекции точек А и В на новую плоскость согласно алгоритма. |А4В4| = |АВ|.
Рис. 7.2
Задача. Прямую общего положения, заданную отрезком АВ, сделать проецирующей прямой (рис. 7.3).
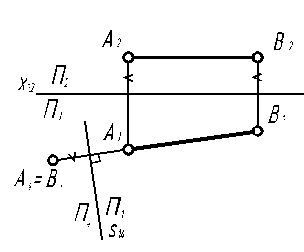Рис. 7.3	Выбор незаменяемой плоскости про­екций в данном случае обусловлен расположением отрезка [АВ], который уже является гори­зонталью. Поэтому незаменяемой оставляем именно горизонтальную плоскость проекций. Алгоритм решения 1. [АВ] || П1 следовательно П1 – const. П2 → П4 ^[АВ] П1 / П2 (x12) → П4 / П1 (s14 ^ [А1В1]). 2. Строим проекции точек A и B на П4 по алгоритму построения точек в дополнительную плоскость. 3. Поскольку П4 ^[АВ], отрезок проецируется в точку.
Если условием задачи предусмотрено превращение прямой общего положения в проецирующую прямую, то сделать это заменой только одной из основных плоскостей проекций нельзя, потому что плоскость, перпендикулярная прямой общего положения, в системе основных плоскостей проекций займет также общее положение и ни с одной из плоскостей не образует новую ортогональную систему плоскостей проекций. Поэтому, чтобы прямую общего положения сделать проецирующей, нужны две последовательных замены обеих основных плоскостей проекций. Сначала заменой одной из плоскостей прямую общего положения делают прямой уровня, а затем заменяют вторую основную плоскость на новую, выставляя ее перпендикулярно прямой.
Задача. Прямую общего положения сделать проецирующей прямой (рис. 7.4).
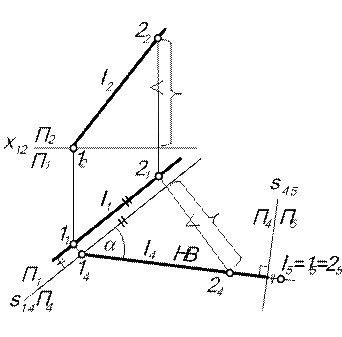
	Алгоритм решения 1. Первая замена: П2 → П4 || l : П1 / П2 (х12)→ П1 / П4 (s14 || l1). Взяв на прямой l две произвольных точки 1 и 2, строим их проекции на П4 по алгоритму построения точек в дополнительную плоскость проекций и соединяем прямой. Поскольку l || П4, отрезок [12] проецируется в П4 в натуральную величину, как и угол a наклона прямой l к П1. 2. Вторая замена: П1 → П5 ^ l: П1 / П4 (s14) → П4 / П5 (s45 ^ l4). Строим проекции точек 1 и 2 на П5 по алгоритму построения точек в дополнительную плоскость проекций, откладывая от оси s45 расстояние от точек до плоскости П4. Поскольку П5 ^ l, то прямая проецируется в точку.
Рис. 7.4
Чертеж, на котором изображены проекции фигур, может быть безосным (не изображена координатная ось х). В этом случае при построениях нужно провести ось для правильного измерения расстояний от точки до плоскостей проекций (ось проекций на чертеже разделяет линию связи, соединяющую две проекции точки, на два отрезка, которые являются соответственно расстояниями от точки до двух плоскостей проекций). Относительно превращения плоскостей: чтобы плоскость общего положения сделать проецирующей, достаточно замены одной из основных плоскостей проекций. Проецирующая плоскость должна проходить через проецирующую прямую. Чтобы новая плоскость проекций была перпен­дикулярна одновременно заданной плоскости общего положения и незаменяемой основной плоскости проекций, в заданной плоскости проводят прямую уровня (смотри рис. 7.3), параллельную незаменяемой плоскости проекций, и новую плоскость проводят перпендикулярно этой прямой. Чтобы плоскость общего положения сделать плоскостью уровня необходимы последовательные замены обеих основных плоскостей проекций: первой заменой плоскость общего положения делают проецирующей, а затем заменяют вторую основную плоскость проекций, выставляя новую плоскость проекций параллельно заданной плоскости.
Задача. Проецирующую плоскость сделать плоскостью уровня (рис. 7.5). Определитель плоскости, которой принадлежит треугольник АВС, в горизонтальной плоскости проекций вырождается в отрезок, расположенный не параллельно оси проекций, потому заданная плоскость является горизонтально-проецирующей. Исходя из этого необходимо из двух плоскостей проекций оставить неизменной именно П1, поскольку заданная плоскость ей уже перпендикулярна. Тогда новая плоскость проекций, которая выставляется параллельно треугольнику, будет тоже перпен­дикулярна П1.
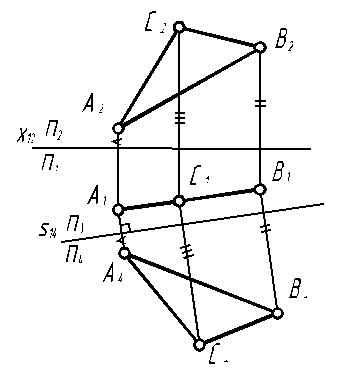
	Алгоритм решения 1. Σ (Δ АВС)^ П1 Þ П1 – const П2 → П4 || D ABC: П1 / П2 (x12)→ П4 / П1 (s14 || [А1 В1]). 2. Строим по алгоритму построения точек в дополнительную плоскость П4 проекции вершин D ABC. Поскольку плоскость D ABC параллельна новой плоскости проекций, то треугольник отображается в П4 в натуральную величину.
Рис. 7.5
Рассмотренные задачи применяют для определения НВ отрезков и углов наклона прямой относительно плоскости проекций, НВ расстояния между точкой и прямой, двумя параллельными прямыми, точкой и плоскостью, углов наклона плоскости к плоскостям проекций, НВ плоской фигуры и тому подобное.