НА ГЛАВНЫХ ПЛОЩАДКАХ.
ПРОВЕРКА ПРОЧНОСТИ (ЗАДАЧА № 8)
Условие задачи
На гранях элементарного параллелепипеда заданы главные напряжения (рис. 2.14). Материал элемента – чугун c характеристиками 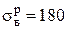 МПа,
МПа, 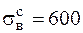 МПа,
МПа, 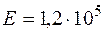 МПа,
МПа, 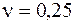 . Нормативный коэффициент запаса прочности
. Нормативный коэффициент запаса прочности 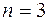 .
.
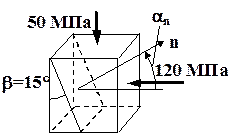 Рис. 2.14.
Условие задачи № 8
Рис. 2.14.
Условие задачи № 8
|
Требуется:
1) найти нормальное 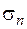 , касательное
, касательное 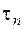 и полное
и полное 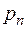 напряжения на наклонной площадке, заданной углом
напряжения на наклонной площадке, заданной углом 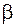 и изображенной на рис. 2.14;
и изображенной на рис. 2.14;
2) найти величины наибольшего касательного напряжения и соответствующего ему нормального напряжения, показать положение площадки, на которой эти напряжения действуют;
3) проверить прочность материала; найти действительный коэффициент запаса прочности.
Решение
Заданный элемент ограничен главными площадками, поэтому сразу пронумеруем главные напряжения по убыванию ( 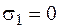 ,
, 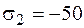 МПа,
МПа,  МПа) и изобразим на рисунке главные оси (рис. 2.15).
МПа) и изобразим на рисунке главные оси (рис. 2.15).
 Рис. 2.15. Уточнение
условия задачи
Рис. 2.15. Уточнение
условия задачи
|
Определение напряжений.Напряжения на наклонной площадке вычисляются так же, как в задаче № 7. Единственное отличие состоит в том, что можно использовать частный случай (2.4) общих формул (2.2а) и (2.2б). Положение наклонной площадки будем задавать углом  , отсчитываемым от оси 3 к нормали n. Значение
, отсчитываемым от оси 3 к нормали n. Значение 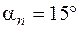 положительно, так как угол отсчитывается против часовой стрелки.
положительно, так как угол отсчитывается против часовой стрелки.
Согласно (2.4)
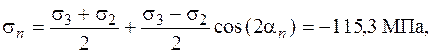
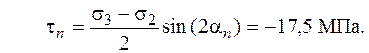
Модуль полного напряжения
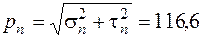 МПа.
МПа.
Примененная формула для касательного напряжения 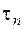 справедлива для площадок, перпендикулярных плоскости чертежа. Максимальное для таких площадок касательное напряжение
справедлива для площадок, перпендикулярных плоскости чертежа. Максимальное для таких площадок касательное напряжение
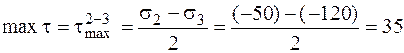 МПа.
МПа.
Соответствующее нормальное напряжение
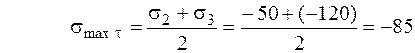 МПа.
МПа.
Подсчитанное выше значение касательного напряжения 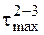 не самое большое из всех возможных значений. Это значение является максимумом для касательных напряжений по площадкам, перпендикулярным плоскости чертежа. Площадка, на которой действует
не самое большое из всех возможных значений. Это значение является максимумом для касательных напряжений по площадкам, перпендикулярным плоскости чертежа. Площадка, на которой действует 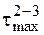 , расположена под углом 45° к главным площадкам 2, 3 (рис. 2.16).
, расположена под углом 45° к главным площадкам 2, 3 (рис. 2.16).
 Рис. 2.16. Площадка
с максимальным касательным напряжением
Рис. 2.16. Площадка
с максимальным касательным напряжением 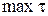
|
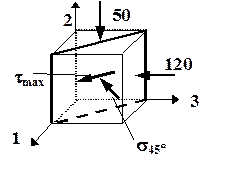 Рис. 2.17. Площадка
с максимальным касательным напряжением
Рис. 2.17. Площадка
с максимальным касательным напряжением 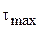
|
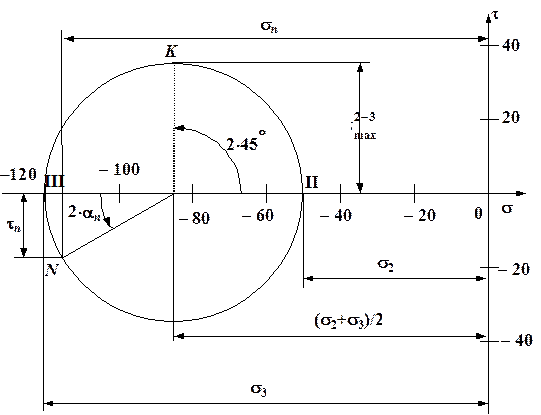 Рис. 2.18. Круг Мора, изображающий заданное плоское
напряженное состояние
Рис. 2.18. Круг Мора, изображающий заданное плоское
напряженное состояние
|
Максимальное касательное напряжение (максимум вычисляется для всех возможных площадок, проведенных через точку) и соответствующее ему нормальное напряжение имеют величины
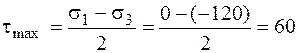 МПа,
МПа,
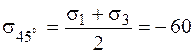 МПа
МПа
и действуют на площадке, перпендикулярной второй главной площадке и повернутой на угол в 45° к первой и третьей главным площадкам (рис. 2.17). Заметим особо, что теперь, в отличие от результата в задаче № 7, 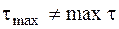 .
.
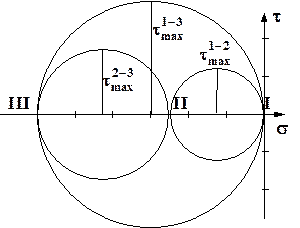 Рис. 2.19. Круги Мора,
изображающие заданное объемное напряженное состояние
Рис. 2.19. Круги Мора,
изображающие заданное объемное напряженное состояние
|
Круг напряжений для заданного плоского напряженного состояния показан на рис. 2.18. Координаты точки 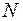 дают значение напряжений на площадке с нормалью n. Площадке с
дают значение напряжений на площадке с нормалью n. Площадке с 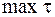 соответствует точка
соответствует точка 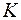 круга.
круга.
На рис. 2.19 показаны все три круга напряжений. Видно, что площадке с наибольшим по модулю касательным напряжением 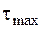 соответствует точка, лежащая на бóльшем круге напряжений.
соответствует точка, лежащая на бóльшем круге напряжений.
Проверка прочности. По условию задачи материал элемента хрупкий. При проверке прочности используем теории прочности, относящиеся к хрупким материалам.
Расчетное напряжение, соответствующее первой теории прочности
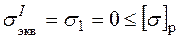 .
.
Видим, что первая теория прочности не годится для оценки прочности, так как она выдает в рассматриваемой ситуации неправдоподобный результат: при любом уровне напряжений прочность обеспечена.
Расчетное напряжение, соответствующее второй теории прочности,
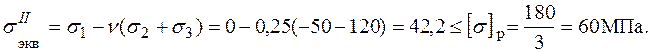 Прочность обеспечена с фактическим коэффициентом запаса
Прочность обеспечена с фактическим коэффициентом запаса
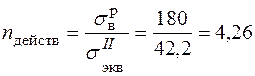 ,
,
большем нормативного ( 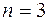 ).
).
Расчетное напряжение, соответствующее теории прочности
Мора,
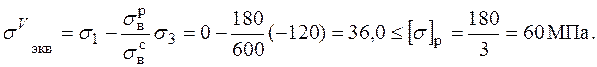
Прочность обеспечена. Фактический коэффициент запаса
 Рис. 2.20. Опасная площадка
по первой и второй теориям
прочности
Рис. 2.20. Опасная площадка
по первой и второй теориям
прочности
|
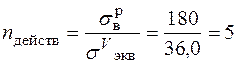 .
.
Опасная плоскость показана на рис. 2.20 жирной линией. Она перпендикулярна первому главному направлению. Если напряженное состояние достигнет критического уровня (для этого все напряжения надо увеличить в 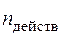 раз), то по указанной плоскости произойдет разрушение.
раз), то по указанной плоскости произойдет разрушение.
Дата добавления: 2016-04-11; просмотров: 903;
