Интерпретация главных компонент

5.13 Свойства главных компонент таковы, что каждая из них описывает некоторую закономерность изменчивости и коррелированности исходных признаков. Выяснение смысла любой такой закономерности возможно при рассмотрении соответствующего

- 78 -

собственного вектора, величины и знаков его элементов у разных исходных показателей.

Рассмотрим простейший случай двух признаков: X₁ – длины тела и X₂ – акромиаль-ного диаметра. Пусть они выражены в нормированном виде z₁ и z₂. Коэффициент корреляции между ними равен 0.56. Значения двух главных компонент для этого простейшего случая можно получить по формулам (5.20). Для интерпретации величин главных компонент будет удобнее, если они будут получаться не только в центрированном, но и в нормированном виде с единичной дисперсией. Этого можно добиться, если использовать формулы

(z₁ + z₂)

y₁ =

[2 (1 + r)]^1/2 (5.32)

(z₁ - z₂)

y₂ =

[2 (1 - r)]^1/2

Будем придавать исходным значениям признаков некоторые фиксированные значения, так чтобы морфологический смыл полученных сочетаний был бы ясен. Одновременно будем рассматривать получающиеся значения главных компонент.

1. Пусть z₁ = 2 и z₂ = 2. Это означает, что по каждому признаку наблюдение отклоняется от средней в сторону больших значений на два средних квадратических отклонения. Для нормального распределения лишь 2.28% всех возможных индивидуальных случаев может отклониться еще дальше от средней в сторону больших значений признаков. Таким образом, принятые значения z₁ и z₂ соматически соответствуют весьма высокорослому и широкоплечему (макроскелетному) индивиду. Величина первой главной компоненты при этом равна

(2 + 2)

y₁ = = 2.26

[2 (1 + 0.56)]^1/2

Таким образом, по первой главной компоненте индивид отклонится от средней в сторону больших значений на 2.26 величин среднего квадратического отклонения. Еще дальше него от центральной точки удалится всего лишь 1.19% всех индивидов. Таким образом, по значениям y₁ этот индивид отклонится от средней еще дальше чем по каждому из исходных признаков.

2. Пусть z₁ = -2 и z₂ = -2.. Это означает, что по каждому признаку наблюдение удаляется от средней величины в сторону малых величин на два средних квадратических отклонения. По каждому признаку лишь 2.28% всех возможных наблюдений отклонится еще дальше в сторону их малых величин. Соматически этот вариант соответствует крайне низкорослому и узкоплечему (микроскелетному) индивиду. Величина первой главной компоненты для этого варианта равна y₁ = -2.26 и это значение удаляется в сторону малых значений гораздо сильнее, чем по каждому из исходных признаков.

Из простого сопоставления хорошо видно, что первая главная компонента принимает большие значения при явной макроскелетности и малые - при микроскелетности. Очевидно, что ее можно интерпретировать как показатель общей величины скелета, развитие которого оценивается по двум его размерам. Следует заметить, что различия поляр-

- 79 -

ных вариантов по первой главной компоненте (4.52 величины среднего квадратического отклонения) оказываются значительно выше, чем по любому признаку (4.00 внутригрупповой "сигмы"). К аналогичному выводу можно придти, если анализировать нагрузки на эту главную компоненту - коэффициенты корреляции с ней у исходных признаков. Вектор нагрузок равен a₁ = (l₁)^1/2b₁

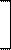
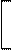1/(2)^1/2 0.88

a₁= (1 + 0.56)^1/2 =

1/(2)^1/2 0.88

Оба признака сильно и положительно скоррелированы с первой главной компонентой и ясно, что она примет максимальное значение, если оба признака одновременно достигнут своих максимумов. Аналогично, минимум первой главной компоненты будет соответствовать индивиду с самыми малыми значениями признаков.

3. Пусть теперь z₁ = 2 и z₂ = -1, что соответствует весьма высокорослому и довольно узкоплечему индивиду, соматически расцениваемому как обладающему долихоморфией своих продольно-поперечных пропорций тела. Значение второй главной компоненты равно

(2 - (-1))

y₂ = = 3.20

[2 (1 - 0.56)]^1/2

По этому значению данный вариант уклоняется в сторону больших величин y₂ так далеко, что еще дальше него оказываются только 0.07% всех возможных наблюдений.

4. Пусть z₁ = -1 и z₂ = 2, что соответствует довольно невысокому и весьма широкоплечему индивиду, которого по пропорциям тела можно считать брахиморфным. Значение второй главной компоненты равно -3.20.

Таким образом, долихоморфные и брахиморфные индивиды характеризуются по значениям второй главной компоненты крайне значительными отклонениями от центра в противоположных направлениях. Следовательно, вторая главная компонента выделяет на полюсах своих значений долихо- и брахиморфные варианты и может считаться показателем продольно-поперечных пропорций тела. Аналогичный вывод мы получим при рассмотрении корреляций y₂ с признаками. Набор нагрузок на вторую главную компоненту равен

0.47

a₂=

-0.47

Нетрудно видеть, что большие положительные значения вторая главная компонента примет при сочетании больших величин длины тела с малыми - акромиального диаметра. При обратном сочетании значений признаков y₂ достигнет больших отрицательных величин.

5.14 Выясним место главных компонент среди других методов, описывающих различия соотношений признаков. Пусть имеется два размера тела, один из которых характеризует его продольное развитие, другой - поперечное. Тогда любой индивид может быть представлен по этим признакам как прямоугольник. Два прямоугольника будут геометрически подобными, если для их сторон справедливо постоянство соотношения

- 80 -

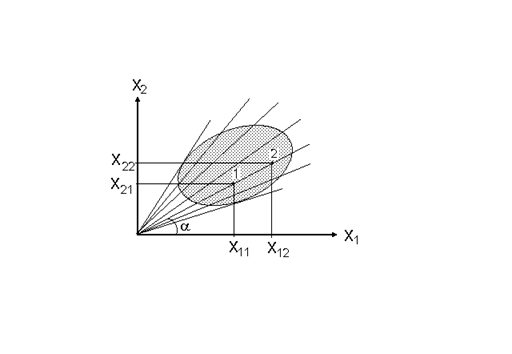
Рисунок 5.5.Описание соотношения двух признаков X₁ и X₂ по методу индексов

X₂₁ X₂₂

= = k , (5.33)

X₁₁ X₁₂

где X₁₁ и X₁₂ - значения первого признака у двух индивидов, X₂₁ и X₂₂ - аналогичные значения второго признака, k - коэффициент геометрического подобия, фактически являющийся простейшим индексом k = I = X₂/X₁. Два индивида считаются имеющими сходное сочетание двух признаков или одинаковую форму тела, если у них одинакова величина этого индекса. Совокупность всех вариантов с одинаковой величиной индекса лежит на некоторой линии с величиной I = tg a (рис.5.5). Такая линия может быть названа линией изоморфии, так как она включает взаимно изоморфные (имеющие одинаковую форму) варианты.

Метод индексов по существу дает описание всех индивидуальных наблюдений с применением системы линий изоморфии, различающихся значением индекса I и соответствующего ему угла наклона a. Изменчивость этого угла измеряет, таким образом, вариацию формы тела. По существу, здесь мы используем так называемую полярную систему координат, когда расположение некоторой точки задается значением некоторой переменной (X₁) и углом a, который составляет вторая ось, соединяющая эту точку с нулем (X₁ = = 0).

Выясним условия постоянства величины индекса - изоморфии. Пусть X₁₂ = X₁₁ + DX₁ и X₂₂ = X₂₁ + DX₂ и пусть различия двух наблюдений DX₁ и DX₂ соотносятся как DX₂ = = а DX₁, где a - некоторая величина. Тогда для того, чтобы два варианта имели одинаковые значения индекса требуется соблюдение

- 81 -

X₂₁ X₂₁ + DX₂ kX₁₁ + a DX₁

k = = = ,

X₁₁ X₁₁ + DX₁ X₁₁ + DX₁

откуда следует выполнение равенства k = a. Таким образом, индекс у двух наблюдений окажется одинаковым, если отношение различий этих вариантов по двум признакам a = DX₂ / DX₁ окакзывается равным значению этого индекса I = k.

Индексы могут использоваться для определения соотношений двух размеров не только у людей, животных, или растений, но также и объектов неживой природы, абстрактных геометрических фигур и т.д. Однако, применительно к объектам живой природы метод индексов имеет целый ряд определенных недостатков. Так, он не учитывает специфических закономерностей варьирования и корреляции признаков. При условии , что k = = DX₂ / DX₁ изменения отдельных признаков DX₂ и DX₁ могут составлять различную долю от величины своей вариации (от величины среднего квадратического отклонения) и в силу этого они могут иметь разный морфологический смысл.

Другим отрицательным свойством индексов является наличие корреляции между величиной индекса и значением признака, стоящего в знаменателе. По смыслу конструкции индекса деление одного признака X₂ на другой - X₁ должно устранить влияние X₁ на X₂ таким образом, чтобы относительная величина I = X₂ / X₁ была бы не связанной с X₁ . Однако, для большинства индексов, применяемых в практике антропологических исследований, этого обычно не достигается.

Например, для индекса акромиального диаметра к длине тела, измеряющего одно из важных свойств пропорций тела - относительную ширину плеч, для выборки взрослых мужчин можно найти отрицательную прямолинейную связь с длиной тела со стандартизованным коэффициентом регрессии -0.14. Это означает, что при увеличении длины тела на одно среднее квадратическое отклонение величина индекса автоматически уменьшается в среднем на 0.14 своей "сигмы". При изменении длины тела от очень малых до очень больших значений (на 4 - 6 "сигм") это уменьшение относительной широкоплечести составит уже весьма заметную величину 0.6 - 0.8 его среднего квадратического отклонения.

Для индекса длины корпуса к длине ноги, измеряющего относительную длину нижней конечности, обнаруживается отрицательная связь с длиной ноги, имеющая стандартизованный коэффициент регрессии -0.73. При изменении длины ноги на 4 – 6 "сигм" автоматическое уменьшение индекса составит 2.9 - 4.4 его среднего квадратического отклонения.

Третий недостаток индексов заключается в обычно проявляющейся его гетероскедастичности в зависимости от значений признака, стоящего в знаменателе (X₁ ). Обычно вариация индекса в области малых значений признака X₁ оказывается большей чем для больших величин X₁ . Этот эффект связан со способом описания точек корреляционного поля, соответствующих наблюдениям, при помощи совокупности линий изоморфии. Нетрудно видеть (рис.5.5), что разнообразие этих линий в области малых значений X₁ оказывается гораздо большим, чем в зоне больших величин X₁ . Наконец, индекс I = X₂ / X₁ включает только два признака. При необходимости увеличения числа одновременно рассматриваемых показателей число их попарных сочетаний очень быстро возрастает, и многомерное обобщение оказывается крайне затруднительным.

- 82 -

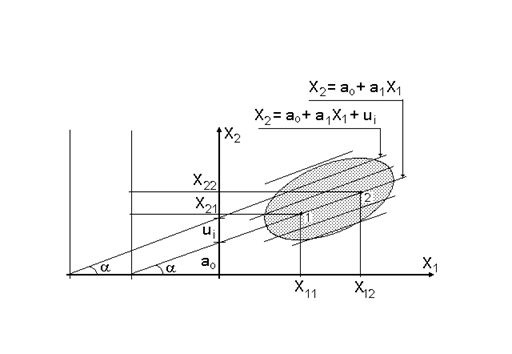
Рисунок 5.6.Описание соотношения двух признаков X₁ и X₂ по методу регрессии

5.15 Отсутствие у метода индексов учета реально существующих закономерностей изменчивости и коррелированности входящих в него признаков потребовало альтернативных подходов, одним из которых стал метод регрессии. Для антропологических показателей часто наблюдается приблизительная прямолинейность связей и для регрессионного ее описания наиболее часто применялась прямолинейная модель X₂ = a_o + a₁ X₁ . Характеристика соотношения двух признаков, построенная по методу регрессии, основана по существу на использовании индекса более сложного вида

I = (X₂ – c) / X₁ , (5.34)

где c - некоторая величина. Пусть I = a₁ - коэффициенту прямолинейной регрессии, c = a_o - свободному члену регрессионного уравнения. Тогда индекс (5.34), превратившийся в уравнение регрессии, опишет некоторую линии изоморфии, совпадающую с линией регрессии (рис.5.6). Для всех вариантов, находящихся на этой линии, можно констатировать средний вариант соотношений двух признаков, соответствующий реальной форме связи между ними. Как видно из рисунка 5.6, геометрическое подобие вариантов 1 и 2 равносильно подобию двух прямоугольников со сторонами X₂₁, X₁₁ + b_o (1-е наблюдение) и X₂₂, X₁₂ + b_o (2-е наблюдение). Величина b_o может быть получена как

a_o

b_o = a_o ctg a = ,

a₁

так как коэффициент регрессии a₁ = tg a.

Пусть теперь в выражении (5.34) I = a₁ и c = a_o + u_i. Тогда мы получим новую линию изоморфии, описываемую уравнением X₂ = a_o + a₁X₁ + u_i . Любые две точки на этой линии будут соответствовать двум прямоугольникам со сторонами X₂₁, X₁₁ + b и X₂₂, X₁₂ +

- 83 -

+ b, где b = (a_o+ u_i )ctg a = (a_o+ u_i )/a₁. В зависимости от величины u_i можно получить различные линии изоморфии, которые будут параллельными линии регрессии. По своему смыслу значения u_i точно соответствуют остаткам в регрессионной модели. Иными словами, любая линия изоморфии, характеризующаяся определенной величиной u_i включает все варианты, которые отклоняются от линии регрессии на u_i . Различные значения u_i будут характеризовать в одних случаях брахиморфию, в других - долихоморфию, в зависимости от того, какой знак примет регрессионный остаток u_i . Таким образом, изменчивость формы при описании ее по методу регрессии - это частная изменчивость зависимого признака X₂.

Использование метода регрессии позволяет добиться независимости показателя формы и признака, влияние которого исключается. Кроме того, здесь изоморфные варианты различаются по значениям признаков морфологически соразмерно. Действительно, условие подобия двух вариантов можно записать как

X₂₁ - (a_o + a₁X₁₁) = X₂₂ - (a_o + a₁X₁₂) = u_i .

Так как a₁ = r s₂ / s₁, это равносильно

X₂₁ - X₂₂ X₁₁ - X₁₂

= r . (5.35)

s₂ s₁

Иными словами, различия значений двух признаков относительно их средних квадратических отклонений у изоморфных вариантов, определяемых по методу регрессии, пропорциональны коэффициенту корреляции этих признаков.

Методу регрессии свойственен один недостаток, заключающийся в логической неадекватности реальным ситуациям, встречающимся на практике. По смыслу этого метода один признак считается независимым, другой - зависящим от него. Такая ситуация действительно встречается, когда один признак является`фактором, значения которого контролируются исследователем, или если вариация какого-то показателя есть причина изменчивости другого признака. В большинстве случаев оба признака не связаны прямыми причинностными связями и выбор независимого признака оказывается логически неопределенным, что допускает субъективизм решения.

5.16 Попытаемся найти подход к оценке различий формы, свободный от недостатков метода регрессии, но обладающий его достоинствами. Будем считать морфологически соразмерными такие изменения двух признаков, когда они составляют одинаковую долю своих средних квадратических отклонений. Тогда условием изоморфии двух вариантов, описываемых двумя признаками, будет морфологическая соразмерность у них различий этих признаков, выражаемая простым равенством

X₂₁ - X₂₂ X₁₁ - X₁₂

= . (5.36)

s₂ s₁

Это условие похоже на равенство (5.35), следующее из регрессионного подхода. Фор-мула (5.36) может быть преобразована к виду

(X₂₁ - M₂) - (X₂₂ - M₂) (X₁₁ - M₁) - (X₁₂ - M₁)

= ,

s₂ s₁

- 84 -

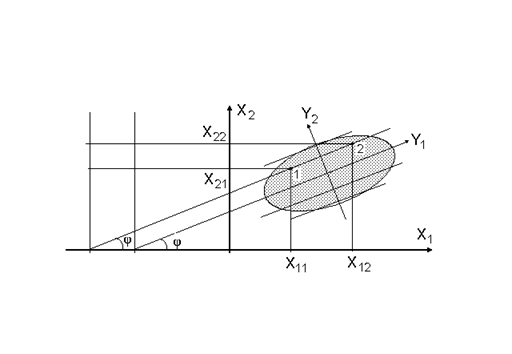
Рисунок 5.7.Описание соотношения двух признаков X₁ и X₂ по методу главных компонент

где M₁ и M₂ - средние значения признаков. Тогда можно записать равенство

z₁₁ - z₁₂ = z₂₁ - z₂₂ ,

где z_ij - нормированные значения признаков. Это также означает справедливость

z₁₁ - z₂₁ = z₁₂ - z₂₂ ,

которое не измениться при домножении обеих его частей на константу 1 / ( 2)^1/2 из формулы (5.20). Тогда с учетом этой последней формулы, можно записать выражения

Y₂₁ = (z₁₁ - z₂₁) ,

( 2)^1/2

Y₂₂ = (z₁₂ – z₂₂)

(2)^1/2

и их равенство

Y₂₁ = Y₂₂.

Таким образом, простейшее условие изоморфии двух вариантов (5.36) означает равенство для этих вариантов значений второй главной компоненты, найденной для нормированных значений признаков. (рис.5.7), но ориентированные вдоль первой оси корреляционного эллипса. Они различаются по значениям второй главной компоненты - показателю соотношений двух признаков. Характеристика формы, построенная по методу главных компонент, свободна от необходимости выделения независимых и зависящих от них признаков. Многомерное обобщение рассмотренной простейшей ситуации возможно на случай практически любого количества показателей.

- 85 -

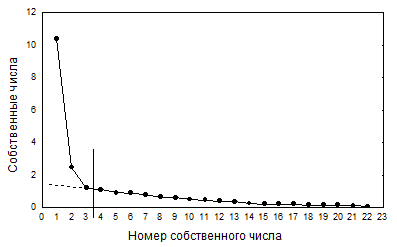
Рисунок 5.8. График значений 22 собственных чисел, найденных при компонентном анализе размеров тела в выборке 242 женщин

Аналогично тому, как это было при использовании метода регрессии, в применении главных компонент для описания формы используются параллельные линии изоморфии.

Кроме условия постоянства формы, оцениваемой по сочетанию двух признаков, можно также рассмотреть понятие постоянства общей величины системы этих признаков - изометрии. Два варианта будем считать изометричными, если увеличение одного признака компенсируется морфологически соразмерным уменьшением - другого. Это можно выразить равенством

X₂₁ - X₂₂ X₁₁ - X₁₂

= - , (5.37)

s₂ s₁

откуда следует z₁₁ - z₁₂ = -(z₂₁ - z₂₂) или z₁₁ + z₂₁ = z₁₂ + z₂₂ .