Условие незаклинивания заготовок при их движении по наклонному лотку

Рис. 16.3. Расчетная схема для определения ширины лотка (гладкая деталь катится по дну лотка)
Пусть по наклоненному лотку перемещается цилиндрическая заготовка диаметром d. Зазор между боковыми стенками лотка и заготовкой
S = B – l
Заготовка может касаться стенок лотка в двух точках: 1 и 2. Зазор S следует выбирать таким, чтобы не было заклинивания.
Если угол перекоса заготовки γ окажется меньше или равным углу трения 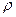 , то заготовка заклинится в лотке.
, то заготовка заклинится в лотке.
tgγ ≤ tg 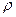 = μ .
= μ .
Если больше – то будет перемещаться по лотку без заклинивания, т.е.
tgγ > tg 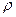 = μ .
= μ .
Условия начала заклинивания
tgγ = tg 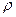 = μ,
= μ,
μ – коэффициент трения.
Из рисунка можно получить: 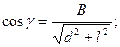
Из тригонометрии известно, что 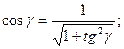
при заклинивании, т.е. при tg γ = μ, получим 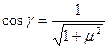 ,
,
Тогда 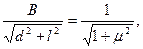
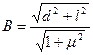 .
.
Чтобы заготовка не заклинивалась, следует уменьшить зазор между нею и боковыми сторонами лотка. Это получится, если выбранная ширина лотка B будет меньше ее значения, соответствующего заклиниванию, и в тоже время больше
l + Smin
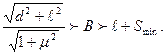
Обычно в левую часть неравенства вставляют наименьшие предельные значения (d и 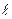 , а Smin берут из
, а Smin берут из 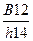 ). Расчет правой и левой части дает пределы, в которых должна находиться ширина лотка B.
). Расчет правой и левой части дает пределы, в которых должна находиться ширина лотка B.
В случае перемещения ступенчатой заготовки по лотку (рис. 16.4) в формулу для определения B входит диаметр Dф.

Рис.16.4. Расчетная схема для определения ширины лотка в случае перемещения ступенчатой заготовки
Случай, когда по лотку перемещается заготовка с цапфами (рис. 16.5).
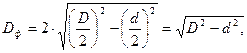
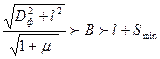

Рис.16.5. Перемещение ступенчатой заготовки, опирающейся цапфами о бортик лотка
Дата добавления: 2016-04-11; просмотров: 1536;
