Лекция 8. Дискретно – стохастические модели
(Р-схемы)
К дискретно – стохастической модели относится вероятностный автомат. В общем, виде вероятностный автомат является дискретным потактным преобразователем информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Поведение автомата зависит от случайного выбора.
Применение схем вероятностных автоматов имеет важное значение для проектирования дискретных систем, в которых проявляется статистически закономерное случайное поведение.
Для Р-автомата вводится аналогичное математическое понятие, как и для F-автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (xi ,zs ), где xi и zs элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции 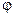 и
и 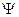 , что с их помощью осуществляется отображение
, что с их помощью осуществляется отображение  и
и 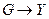 , то говорят, что
, то говорят, что 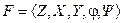 определяет автомат детерминированного типа.
определяет автомат детерминированного типа.
Функция переходов вероятностного автомата определяет не одно конкретное состояние, а распределение вероятностей на множестве состояний (автомат со случайными переходами). Функция выходов также есть распределение вероятностей на множестве выходных сигналов (автомат со случайными выходами).
Для описания вероятностного автомата введем в рассмотрение более общую математическую схему. Пусть Ф – множество всевозможных пар вида (zk ,yj), где yj – элемент выходного подмножества Y. Далее потребуем чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:
элементы из Ф ... 
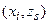 ...
... 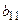
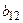 ...
... 
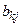 ,
,
где 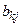 – вероятности перехода автомата в состояние zk и появления на выходе сигнала yj , если он был в состоянии zs и на его вход в этот момент времени поступал сигнал xi.
– вероятности перехода автомата в состояние zk и появления на выходе сигнала yj , если он был в состоянии zs и на его вход в этот момент времени поступал сигнал xi.
Число таких распределений , представленных в виде таблиц равно числу элементов множества G. Если обозначить это множество таблиц через В, то тогда четверку элементов 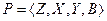 называют вероятностным автоматом (Р-автоматом). При этом
называют вероятностным автоматом (Р-автоматом). При этом
 .
.
Частным случаем Р-автомата, задаваемого как 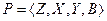 являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминировано (Z-детерминированный вероятностный автомат, Y-детерминированный вероятностный автомат соответственно).
являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминировано (Z-детерминированный вероятностный автомат, Y-детерминированный вероятностный автомат соответственно).
Очевидно, что с точки зрения математического аппарата задание Y-детерминированного Р-автомата эквивалентно заданию некоторой марковской цепи с конечным множеством состояний. В связи с этим аппарат марковских цепей является основным при использовании Р-схем для аналитических расчетов. Подобные Р-автоматы используют генераторы марковских последовательностей при построении процессов функционирования систем или воздействий внешней среды.
Марковские последовательности, согласно теореме Маркова, – это последовательность случайных величин, для которой справедливо выражение
 ,
,
где N – количество независимых испытаний; D – дисперсия.
Такие Р-автоматы (Р-схемы) могут быть использованы для оценки различных характеристик исследуемых систем как для аналитических моделей, так и для имитационных моделей с использованием методов статистического моделирования.
Y-детерминированный Р-автомат можно задать двумя таблицами: переходов (табл. 1) и выходов (табл.2).
Таблица 1
| zk | zk | ||||
| z1 | z2 | ... | zk-1 | zk | |
| z1 | P11 | P12 | ... | P1(k-1) | P1k |
| z2 | P21 | P22 | ... | P2(k-1) | P2k |
| ... | ... | ... | ... | ... | ... |
| zk | Pk1 | Pk2 | ... | Pk(k-1) | Pkk |
Таблица 2
| Z... | z1 | z2 | ... | zk-1 | zk |
| Y... | yi1 | yi2 | ... | yi(k-1) | yik |
где Pij – вероятность перехода Р-автомата из состояния zi в состояние zj, при этом
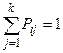 .
.
Таблицу 1 можно представить в виде квадратной матрицы размерности 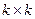 . Такую таблицу будем называть матрицей переходных вероятностей или просто матрицей переходов Р-автомата, которую можно представить в компактной форме:
. Такую таблицу будем называть матрицей переходных вероятностей или просто матрицей переходов Р-автомата, которую можно представить в компактной форме:
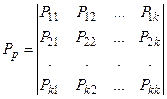 .
.
Для описания Y-детерминированного Р-автомата необходимо задать начальное распределение вероятностей вида:
| Z... | z1 | z2 | ... | zk-1 | zk |
| D... | d1 | d2 | ... | dk-1 | dk |
где dk – вероятность того, что в начале работы Р-автомат находится в состоянии zk, при этом
 .
.
Итак, до начала работы Р-автомат находится в состоянии z0 и в начальный (нулевой) такт времени меняет состояние в соответствии с распределением D. После этого смена состояний автомата определяется матрицей переходов Р. С учетом z0 размерность матрицы Рр следует увеличить до  , при этом первая строка матрицы будет (d0,d1,d2,...,dk), а первый столбец будет нулевым.
, при этом первая строка матрицы будет (d0,d1,d2,...,dk), а первый столбец будет нулевым.
Пример.Y-детерминированный Р-автомат задан таблицей переходов:
Таблица 3
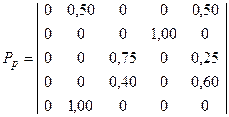
и таблицей выходов
Таблица 4
| Z | 
| 
| 
| 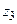
| 
|
| Y |
С учетом таблицы 4 граф переходов вероятностного автомата представлен на рис. 1.

Рис. 1. Граф переходов
Требуется оценить суммарные финальные вероятности пребывания этого автомата в состоянии z2 и z3, т.е. когда на выходе автомата появляются единицы.
При аналитическом подходе можно использовать известные соотношения из теории марковских цепей и получить систему уравнений для определения финальных вероятностей. Причем начальное состояние можно не учитывать в виду того, что начальное распределение не оказывает влияние на значения финальных вероятностей. Тогда таблица 1.3 примет вид:

где 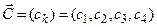 – финальная вероятность пребывания Y-детерминированного Р- автомата в состоянии zk.
– финальная вероятность пребывания Y-детерминированного Р- автомата в состоянии zk.
В результате получаем систему уравнений:
 (3.7)
(3.7)
К данной системе следует добавить условие нормировки:
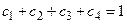 (3.8)
(3.8)
Теперь решая систему уравнений (3.7) совместно с (3.8), получаем:
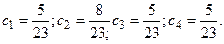
Таким образом, при бесконечной работе заданного автомата на его выходе будет формироваться двоичная последовательность с вероятностью появления единицы, равной:
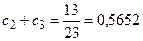 .
.
Для оценки характеристик систем, представленных в виде Р-схем, кроме аналитических моделей можно применять и имитационные модели, реализуемые, например, методом статистического моделирования.
| <== предыдущая лекция | | | следующая лекция ==> |
| Роторно-поступательные насосы | | | Лекция №3. ИЗМЕРИТЕЛЬНЫЕ ГЕНЕРАТОРЫ СИГНАЛОВ НИЗКОЙ ЧАСТОТЫ |
Дата добавления: 2016-04-06; просмотров: 2525;
