Сложение и вычитание. При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков. В процессе выравнивания порядков мантисса

При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.

В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.

В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.

Пример 1. Сложить двоичные нормализованные числа 0.10111^.2^-1 и 0.11011^.2¹⁰. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:

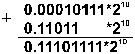
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101^.2¹⁰ и 0.11101^.2¹. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:

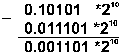
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0.1101^.2⁰.

Умножение

При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.

Пример 3. Выполнить умножение двоичных нормализованных чисел:

(0.11101^.2¹⁰¹)^.(0.1001^.2¹¹) = (0.11101^.0.1001)^.2^(101+11) = 0.100000101^.2¹⁰⁰⁰.

Деление

При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется.

Пример 4. Выполнить деление двоичных нормализованных чисел:

0.1111^.2¹⁰⁰ : 0.101^.2¹¹ = (0.1111 : 0.101) ^.2^(100-11) = 1.1^.2¹ = 0.11^.2¹⁰.

Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.

Упражнения

4.1. Используя Правило Счета, запишите первые 20 целых чисел в десятичной, двоичной, троичной, пятеричной и восьмеричной системах счисления.
[ Ответ ]

4.2. Какие целые числа следуют за числами:

а) 1₂;	е) 1₈;	п) F₁₆;
б) 101₂;	ж) 7₈;	м) 1F₁₆;
в) 111₂;	з) 37₈;	н) FF₁₆;
г) 1111₂;	и) 177₈;	о) 9AF9₁₆;
д) 101011₂;	к) 7777₈;	п) CDEF₁₆ ?

[ Ответ ]

4.3. Какие целые числа предшествуют числам:

а) 10₂;	е) 10₈;	л) 10₁₆;
б) 1010₂;	ж) 20₈;	м)20₁₆;
в) 1000₂;	з) 100₈;	н) 100₁₆;
г) 10000₂;	и) 110₈;	о) A10₁₆;
д) 10100₂;	к) 1000₈;	п) 1000₁₆ ?

[ Ответ ]

4.4. Какой цифрой заканчивается четное двоичное число? Какой цифрой заканчивается нечетное двоичное число? Какими цифрами может заканчиваться четное троичное число?
[ Ответ ]

4.5. Какое наибольшее десятичное число можно записать тремя цифрами:

o а) в двоичной системе;

o б) в восьмеричной системе;

o в) в шестнадцатеричной системе?

[ Ответ ]

4.6. В какой системе счисления 21 + 24 = 100?
Решение. Пусть x — искомое основание системы счисления. Тогда 100_x = 1 · x² + 0 · x¹ + 0 · x⁰, 21_x = 2 · x¹ + 1 · x⁰, 24_x = 2 · x¹ + 4 · x⁰. Таким образом, x² = 2x + 2x + 5 или x² - 4x - 5 = 0. Положительным корнем этого квадратного уравнения является x = 5.
Ответ. Числа записаны в пятеричной системе счисления.

4.7. В какой системе счисления справедливо следующее:

o а) 20 + 25 = 100;

o б) 22 + 44 = 110?

[ Ответ ]

4.8. Десятичное число 59 эквивалентно числу 214 в некоторой другой системе счисления. Найдите основание этой системы.

[ Ответ ]

4.9. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

а) 1011011₂;	е) 517₈;	л) 1F₁₆;
б) 10110111₂;	ж) 1010₈;	м) ABC₁₆;
в) 011100001₂;	з) 1234₈;	н) 1010₁₆;
г) 0,1000110₂;	и) 0,34₈;	о) 0,А4₁₆;
д) 110100,11₂;	к) 123,41₈;	п) 1DE,C8₁₆.

[ Ответ ]

4.10. Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 125₁₀; б) 229₁₀; в) 88₁₀; г) 37,25₁₀; д) 206,125₁₀.

[ Ответ ]

4.11. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 1001111110111,0111₂;	г) 1011110011100,11₂;
б) 1110101011,1011101₂;	д) 10111,1111101111₂;
в) 10111001,101100111₂;	е) 1100010101,11001₂.

[ Ответ ]

4.12. Переведите в двоичную и восьмеричную системы шестнадцатеричные числа:

а) 2СE₁₆; б) 9F40₁₆; в) ABCDE₁₆; г) 1010,101₁₆; д) 1ABC,9D₁₆.
[ Ответ ]

4.13. Выпишите целые числа:

o а) от 101101₂ до 110000₂ в двоичной системе;

o б) от 202₃ до 1000₃ в троичной системе;

o в) от 14₈ до 20₈ в восьмеричной системе;

o г) от 28₁₆ до 30₁₆ в шестнадцатеричной системе.

[ Ответ ]

4.14. Для десятичных чисел 47 и 79 выполните цепочку переводов из одной системы счисления в другую:

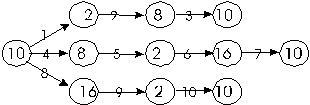
[ Ответ ]

4.15. Составьте таблицы сложения однозначных чисел в троичной и пятеричной системах счисления.
[ Ответ ]

4.16. Составьте таблицы умножения однозначных чисел в троичной и пятеричной системах счисления.
[ Ответ ]

4.17. Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а) 1011101₂ и 1110111₂;	д) 37₈ и 75₈;	и) A₁₆ и F₁₆;
б) 1011,101₂ и 101,011₂;	е) 165₈ и 37₈;	к) 19₁₆ и C₁₆;
в) 1011₂, 11₂ и 111,1₂;	ж) 7,5₈ и 14,6₈;	л) A,B₁₆ и E,F₁₆;
г) 1011₂ , 11,1₂ и 111₂;	з) 6₈, 17₈ и 7₈;	м) E₁₆, 9₁₆ и F₁₆.

[ Ответ ]

4.18. В каких системах счисления выполнены следующие сложения? Найдите основания каждой системы:

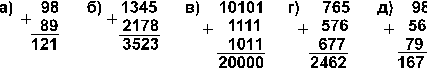
[ Ответ ]

4.19. Найдите те подстановки десятичных цифр вместо букв, которые делают правильными выписанные результаты (разные цифры замещаются разными буквами):

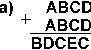
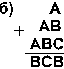
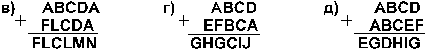
[ Ответ ]

4.20. Вычтите:

а) 111₂ из 10100₂;	д) 15₈ из 20₈;	и) 1А₁₆ из 31₁₆;
б) 10,11₂ из 100,1₂;	е) 47₈ из 102₈;	к) F9E₁₆ из 2А30₁₆;
в) 111,1₂ из 10010₂;	ж) 56,7₈ из 101₈;	л) D,1₁₆ из B,92₁₆;
г) 10001₂ из 1110,11₂;	з) 16,54₈ из 30,01₈;	м) ABC₁₆ из 5678₁₆.

[ Ответ ]

4.21. Перемножьте числа, а затем проверьте результаты, выполнив соответствующие десятичные умножения:

а) 101101₂ и 101₂;	д) 37₈ и 4₈;
б) 111101₂ и 11,01₂;	е) 16₈ и 7₈;
в) 1011,11₂ и 101,1₂;	ж) 7,5₈ и 1,6₈;
г) 101₂ и 1111,001₂;	з) 6,25₈ и 7,12₈.

[ Ответ ]

4.22. Разделите 10010110₂ на 1010₂ и проверьте результат, умножая делитель на частное.
[ Ответ ]

4.23. Разделите 10011010100₂ на 1100₂ и затем выполните соответствующее десятичное и восьмеричное деление.
[ Ответ ]

4.24. Вычислите значения выражений:

o а) 256₈ + 10110,1₂ ^.(60₈ + 12₁₀) - 1F₁₆;

o б) 1AD₁₆ - 100101100₂ : 1010₂ + 217₈;

o в) 1010₁₀ + (106₁₆ - 11011101₂) 12₈;

o г) 1011₂ ^.1100₂ : 14₈ + (100000₂ - 40₈).

[ Ответ ]

4.25. Расположите следующие числа в порядке возрастания:

o а) 74₈, 110010₂, 70₁₀, 38₁₆;

o б) 6E₁₆, 142₈, 1101001₂, 100₁₀;

o в) 777₈, 101111111₂, 2FF₁₆, 500₁₀;

o г) 100₁₀, 1100000₂, 60₁₆, 141₈.

[ Ответ ]

4.26. Запишите уменьшающийся ряд чисел +3, +2, ..., -3 в однобайтовом формате:

o а) в прямом коде;

o б) в обратном коде;

o в) в дополнительном коде.

[ Ответ ]

4.27. Запишите числа в прямом коде (формат 1 байт):

а) 31; б) -63; в) 65; г) -128.
[ Ответ ]

4.28. Запишите числа в обратном и дополнительном кодах (формат 1 байт):

а) -9; б) -15; в) -127; г) -128.
[ Ответ ]

4.29. Найдите десятичные представления чисел, записанных в дополнительном коде:

а) 1 1111000; б) 1 0011011; в) 1 1101001; г) 1 0000000.
[ Ответ ]

4.30. Найдите десятичные представления чисел, записанных в обратном коде:

а) 1 1101000; б) 1 0011111; в) 1 0101011; г) 1 0000000.
[ Ответ ]

4.31. Выполните вычитания чисел путем сложения их обратных (дополнительных) кодов в формате 1 байт. Укажите, в каких случаях имеет место переполнение разрядной сетки:

а) 9 - 2;	г) -20 - 10;	ж) -120 - 15;
б) 2 - 9;	д) 50 - 25;	з) -126 - 1;
в) -5 - 7;	е) 127 - 1;	и) -127 - 1.

[ Ответ ]

<15 16 171819 20 21 >

Дата добавления: 2016-04-06; просмотров: 1032;