Интегральные характеристики пограничного слоя

Возмущения, вносимые в поток обтекаемым телом или стенками каналов, при числах Re 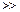1 локализуются в относительно тонких пристенных слоях рабочей среды, что позволяет использовать модель пограничного слоя конечной толщины , за пределами которого течение считается невозмущенным (рис.10.3). Если число Re велико, то на некотором удалении от поверхности рабочую среду можно рассматривать как идеальную, влиянием вязкости которой допускается пренебречь.

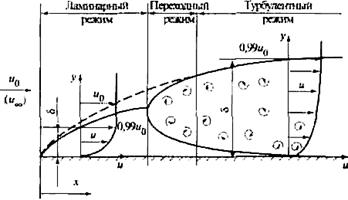
Рис. 10.3. Схема развития пограничного слоя

Основное влияние вязкости сосредоточено в пределах пограничного слоя, где скорость потока по нормали к стенке монотонно изменяется от нуля на стенке (гипотеза прилипания частиц к поверхности) до скорости невозмущенного течения. По аналогии с полем скоростей в динамическом пограничном слое используются модели теплового (поле температур) и диффузионного (поле концентрации вещества при наличии диффузии) пограничных слоев. Так как скорости, температуры и концентрации в пограничном слое стремятся к их значениям во внешнем потоке асимптотически, то точно определить физические толщины соответствующих слоев в опытах крайне сложно. Поэтому за толщины слоев принимают значения координат по нормали к стенке, при которых скорость, температура или концентрация в них отличаются от соответствующих значений этих величин во внешнем потоке на 1 %, т.е. . 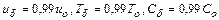Неточности в определении физических толщин пограничных слоев снимаются при использовании их интегральных характеристик, введенных Т.Карманом. Для динамического пограничного слоя интегральные характеристики имеют следующие выражения:

толщина вытеснения

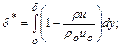(10.9)

толщина потери импульса

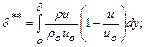(10.10)

толщина потери энергии

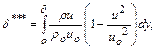(10.11)

где индекс «0» присвоен величинам, характеризующим невозмущенный поток.

При умножении данных толщин на поперечные размеры (периметр) обтекаемого тела получаются интегральные площади, определяющие соответственно расходную, силовую и энергетическую характеристики пограничного слоя. В тепловом и диффузионном пограничных слоях используются аналогичные интегральные толщины. В пределах пограничного слоя возможны как ламинарный, так и турбулентный режимы течения рабочей среды. Что касается напряжения, возникающего вследствие трения, то внутри пограничного слоя оно велико даже при малой вязкости, так как градиент скорости в направлении, перпендикулярном к плоскости стенок, весьма большой.

Методика расчета обтекания тел и течений внутри каналов с учетом интегральных толщин пограничного слоя заключается в следующей последовательности операций:

1) на основе модели идеального газа (жидкости) вычисляется распределение скорости рабочей среды 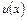и ее термодинамических параметров 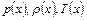по длине тела (канала);

2) полученное распределение 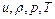используется как первое приближение характеристик внешнего потока на границе пограничного слоя для расчета его интегральных характеристик ;

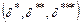3) значения толщины вытеснения 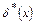позволяют изменить границу твердых стенок в каждом расчетном сечении в сторону движущейся среды по нормали к стенке, т.е. вводится фиктивная поверхность;

4) вновь осуществляется расчет распределений 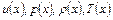для полученных фиктивных поверхностей обтекаемого тела (канала);

5) по распределениям 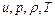второго приближения рассчитываются характеристики пограничного слоя. Обычно второго приближения в расчетах бывает достаточно.

Вычисление интегральных характеристик 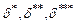осуществляется с учетом таких главных факторов влияния, как режим течения в пограничном слое, градиентность внешнего потока по его длине ( 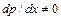), а также многих других особенностей как рабочей среды, так и обтекаемых тел.

Расчет ламинарного и турбулентного пограничных слоев при безградиентном течении рабочей среды (обтекание пластины, течение по плоской поверхности стенки канала, когда 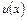=const) осуществляется по выражениям, приведенным в табл.10.1. Здесь используются приближения профиля скорости в пограничном слое на основе степенной зависимости при турбулентном режиме и полинома третьей степени при ламинарном режиме течения. Число 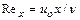вычисляется по линейной координате 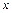в том сечении пластины, где определяются интегральные толщины пограничного слоя. В практических задачах требуется знание коэффициента сопротивления трения 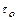(местного коэффициента трения в сечении с координатой 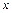пластины). Он позволяет вычислить напряжение трения на стенке в заданном сечении. Для расчета силы трения на участке стенки используется полный (интегральный) коэффициент сопротивления трения .

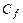Таблица 10.1.

Характеристики пограничного слоя при течении несжимаемой среды

вдоль гладкой плоской стенки

Характеристика	Обозначение	Ламинарный режим	Турбулентный режим
Профиль скорости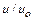
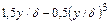
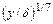
Толщина физическая
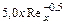
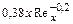
Толщина вытеснения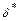
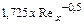
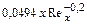
Толщина потери импульса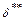
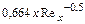
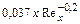
Напряжение трения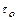
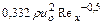
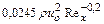
Местный коэффициент трения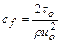
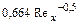
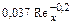
Полный коэффициент трения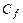

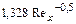
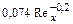
Примечания: 1. Коэффициент сопротивления для шероховатых поверхностей может определяться по формуле .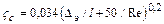

2. Сила трения, действующая на одну сторону пластины длиной 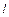и шириной , .

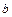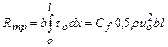Критическое число Рейнольдса для гладкой пластины, определяющее переход к турбулентному режиму течения, можно принимать равным 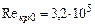. Оценка влияния шероховатости на значение 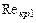осуществляется по зависимости, представленной на рис.10.4, где 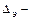эквивалентная шероховатость поверхности.

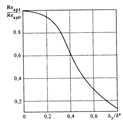
Рис.10.4. Влияние шероховатости на значение при продольном обтекании пластины