кількісні характеристики Надійності

Надійність, як поєднання властивостей безвідмовності, ремонтоспособности, довговічності і сохраняемости, і самі ці якості кількісно характеризуються різними функціями і числовими параметрами. Правильний вибір кількісних показників надійності РЕА дозволяє об'єктивно порівнювати технічні характеристики різних виробів як на етапі проектування, так і на етапі експлуатації (правильний вибір системи елементів, технічні обгрунтування роботи по експлуатації і ремонту РЕА, об'єм необхідного запасного майна і ін.).

Виникнення відмов носить випадковий характер. Процес виникнення відмов в РЕА описується складними імовірнісними законами. У інженерній практиці для оцінки надійності РЕА вводять кількісні характеристики, засновані на обробці експериментальних даних.

Безвідмовність виробів характеризується вірогідністю безвідмовної роботи P(t) (характеризує швидкість зниження надійності в часі), частотою відмов F(t), інтенсивністю відмов l(t), середнім напрацюванням на відмову Тср. Можна також надійність РЕА оцінювати вірогідністю відмови q(t)= 1 - P(t).

Розглянемо оцінку надійності систем, що не ремонтуються. Приведені характеристики вірні і для ремонтованих систем, якщо їх розглядати для випадку до першої відмови.

Хай на випробування поставлена партія, N виробів, що містить. В процесі випробувань до моменту часу t вишли з ладу n виробів. Залишилося справним:

N(t) = N – n.

Відношення Q(t) = n/N є оцінкою вірогідності виходу з ладу виробу за час t. Чим більше число виробів, тим точніше оцінка надійності результатів, строгий вираз для якої виглядає таким чином:

Q(t)= .

Величина P(t), рівна

P(t) = 1 – Q(t)

називається теоретичною вірогідністю безвідмовної роботи і характеризує вірогідність того, що до моменту t не відбудеться відмови.

Вірогідність безвідмовної роботи виробу може бути визначена і для довільного інтервалу часу (t1; t2) з моменту початку експлуатації. В цьому випадку говорять про умовну вірогідність P(t1_; t2₎ в період (t1_; t2₎ при робочому стані у момент часу t1_. Умовна вірогідність P(t1_; t2₎ визначається відношенням:

P(t1; t2)= P(t2)/ P(t1)

де P(t1) і P(t2) - відповідно значення вірогідності на початку (t1) і кінці (t2) напрацювання.

Значення частоти відмов за час t в даному досвіді визначається відношенням F(t) = n/Nt = Q(t) /t. Як показник надійності систем, що не ремонтуються, частіше використовують похідну за часом від функції відмови Q(t), яка характеризує щільність розподілу напрацювання виробу повністю f(t):

F(t)= dQ(t) /dt = - dP(t) /dt.

Величина f(t)dt характеризує вірогідність того, що система відмовить в інтервалі часу (t; t+dt) за умови, що у момент часу t вона знаходилася в робочому стані.

Інтенсивність відмов. Критерієм, що більш повно визначає надійність РЕА, що не ремонтується, і її модулів, є інтенсивність відмов l(t). Інтенсивність відмов (t) lпредставляє умовну вірогідність виникнення відмови в системі в деякий момент часу напрацювання за умови, що до цього моменту відмов в системі не було. Величина (t) lвизначається відношенням

l(t)= f(t) /P(t)= (1/P(t) dQ/dt.

Звідси витікає, що величина (t) dt характеризує умовну вірогідність того, що система відмовить в інтервалі часу (t; t+dt) за умови, що у момент часу t вона знаходилася в працездатному стані. Цей показник характеризує надійність РЕА у будь-який момент часу і для інтервалу Dti може бути обчислений за формулою:

l = Dni /(NсрDti),

де Dni = Ni - Ni+1 - число відмов; Ncp = (Ni + Ni+1)/2 - середнє число працездатних виробів; Ni, і Ni+1 - кількість працездатних виробів на початку і кінці проміжку часу Dti.

Вірогідність безвідмовної роботи пов'язана з величинами (t) і f(t) наступними виразами:

P(t)= exp(-l(t) 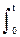dt), P(t)= exp(-f(t) 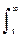dt)

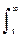
Знаючи одну з характеристик надійності P(t), (t) або f(t), можна знайти дві інші.

Якщо необхідно оцінити умовну вірогідність, можна скористатися наступним виразом:

P(t1; t2)= exp(-l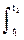(t) dt).

Якщо РЕА містить N послідовно сполучених однотипних елементів, то

lN(t)= Nl(t).

Середнє напрацювання на відмову Тср і вірогідність безвідмовної роботи P(t) зв'язані залежністю

Тср = P(t) dt.

За статистичними даними

Тср = 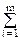Dn_i tсрi, tсрi = (ti+ti+1)/2, m = t/Dt

де Dni - кількість виробів, що відмовили, за інтервал часу Dtсрi = (ti+1-ti); ti, ti+1 - відповідно час на початку і кінці інтервалу випробувань (t1=0); t - інтервал часу, за який відмовили всі вироби; m - число тимчасових інтервалів випробувань.

Приклад. З 20 виробів, що не ремонтуються, в перший рік експлуатації відмовило 10, в другій – 5, в третій - 5. Визначити вірогідність безвідмовної роботи, частоту відмов, інтенсивність відмов в перший рік експлуатації, а також середнє напрацювання до першої відмови.

P=(20-10) /20 = 0.5, f=10/(20·1)= 0.5 г-1

l=10/[(20-10)/2]= 2 г-1, Тср= (10·0.5+5·1.5+5·2.5) /20 = 1.25 р.

Правильно розуміти фізичну природу і суть відмов дуже важливо для обгрунтованої оцінки надійності технічних пристроїв. У практиці експлуатації розрізняють три характерні типи відмов: приработочные, раптові і відмови із-за зносу. Вони розрізняються фізичною природою, способами попередження і усунення і виявляються в різні періоди експлуатації технічних пристроїв.

Відмови зручно характеризувати «кривому життю» виробу, яке ілюструє залежність інтенсивності відмов (t), що відбуваються в нім, від часу t. Така крива, що ідеалізується, для РЕА приведена на малюнку 7.2.1.

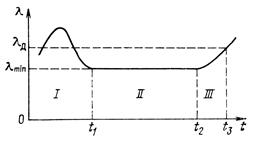Мал. 7.2.1.

Вона має три явно виражених періоду: прироблення I, нормальній експлуатації II, і зносу III.

Приработочна відмова спостерігаються в перший період (0 - t1) експлуатації РЕА і виникають, коли частина елементів, що входять до складу РЕА, є бракованими або мають приховані дефекти. Фізичний сенс приработочных відмов може бути пояснений тим, що електричні і механічні навантаження, що доводяться на компоненти РЕА в приработочный період, перевершують їх електричну і механічну міцність. Оскільки тривалість періоду прироблення РЕА визначається в основному інтенсивністю відмов вхідних в її склад неякісних елементів, то тривалість безвідмовної роботи таких елементів зазвичай порівняно низка, тому виявити і замінити їх вдається за порівняно короткий час.

Залежно від призначення РЕА період прироблення може продовжуватися від декількох до сотень годинників. Чим відповідальніший виріб, тим більше тривалість цього періоду. Період прироблення складає зазвичай долі і одиниці відсотка від часу нормальної експлуатації РЕА в другому періоді.

Як видно з малюнка, ділянка «кривого життя» РЕА, відповідна періоду прироблення I, є монотонно убуваючою функцією (t), крутизна якої і протяжність в часі тим менше, чим досконало конструкція, вище якість її виготовлення і ретельніше дотримані режими прироблення. Період прироблення вважають завершеним, коли інтенсивність відмов РЕА наближається до мінімально досяжної (для даної конструкції) величини min в точці t1_.

Пріработочниє відмови можуть бути наслідком конструкторських (наприклад, невдала компоновка), технологічних (неякісне виконання збірки) і експлуатаційних (порушення режимів прироблення) помилок.

З урахуванням цього, при виготовленні виробів підприємствам рекомендується проводити прогін виробів протягом декількох десятків годин роботи (до 2-5 діб) по спеціально розроблених методиках, в яких передбачається робота при впливі різних дестабілізуючих чинників (цикли безперервної роботи, цикли включень-виключень, зміни температури, напруга живлення і ін.).

Період нормальної експлуатації. Раптові відмови спостерігаються в другий період (t1—t2₎ експлуатації РЕА. Вони виникають несподівано унаслідок дії ряду випадкових чинників, і попередити їх наближення практично не представляється можливим, тим більше що до цього часу в РЕА залишаються тільки повноцінні компоненти. Проте і такі відмови все ж таки підкоряються певним закономірностям. Зокрема, частота їх появи протягом достатнього великого проміжку часу однакова в однотипних класах РЕА.

Фізичний сенс раптових відмов може бути пояснений тим, що при швидкій кількісній зміні (зазвичай - різкому збільшенні) якого-небудь параметра в компонентах РЕА відбуваються якісні зміни, в результаті яких вони втрачають повністю або частково свої властивості, необхідні для нормального функціонування. До раптових відмов РЕА відносять, наприклад, пробій діелектриків, короткі замикання провідників, несподівані механічні руйнування елементів конструкції і тому подібне

Період нормальної експлуатації РЕА характеризується тим, що інтенсивність її відмов в інтервалі часу (t1—t2) мінімальна і має майже постійне значення _lmin » const. Величина _min тим менше, а інтервал (t1 – t2) тим більше, чим досконало конструкція РЕА, вище якість її виготовлення і ретельніше дотримані режими експлуатації. Період нормальної експлуатації РЕА загальнотехнічного призначення може продовжуватися десятки тисяч годинників. Він може навіть перевищувати час морального старіння апаратури.

Період зносу. В кінці рядок служби апаратури кількість відмов знову починає наростати. Вони в більшості випадків є закономірним наслідком поступового зносу і природного старіння використовуваних в апаратурі матеріалів і елементів. Залежать вони головним чином від тривалості експлуатації і «віку» РЕА.

Середній термін служби компоненту до зносу - величина визначеніша, ніж час виникнення приработочных і раптових відмов. Їх появу можна передбачати на підставі досвідчених даних, отриманих в результаті випробувань конкретної апаратури.

Фізичний сенс відмов із-за зносу може бути пояснений тим, що в результаті поступової і порівняно повільної кількісної зміни деякого параметра компоненту РЕА цей параметр виходить за межі встановленого допуску, повністю або частково втрачає свої властивості, необхідні для нормального функціонування. При зносі відбувається часткове руйнування матеріалів, при старінні - зміна їх внутрішніх физико-хімічних властивостей.

До відмов в результаті зносу відносять втрату чутливості, точність, механічний знос деталей і ін. Ділянка (t2—t3) «кривого життя» РЕА, відповідна періоду зносу, є монотонно зростаючою функцією, крутизна якої тим менше (а протяжність в часі тим більше), чим якісніші матеріали і комплектуючі вироби використані в апаратурі. Експлуатація апаратури припиняється, коли інтенсивність відмов РЕА наблизиться до максимально допустимою для даної конструкції.

Вірогідність безвідмовної роботи РЕА. Виникнення відмов в РЕА носить випадковий характер. Отже, час безвідмовної роботи є випадкова величина, для опису якої використовують різні розподіли: Вейбулла, експоненціальний, Пуассона.

Відмови в РЕА, що містить велике число однотипних елементів, що не ремонтуються, досить добре підкоряються розподілу Вейбулла. Експоненціальний розподіл заснований на припущенні постійної в часі інтенсивності відмов і успішно може бути використано при розрахунках надійності апаратури одноразового застосування, що містить велике число компонентів, що не ремонтуються. При тривалій роботі РЕА для планування її ремонту важливо знати не вірогідність виникнення відмов, а їх число за певний період експлуатації. В цьому випадку застосовують розподіл Пуассона, що дозволяє підрахувати вірогідність появи будь-якого числа випадкових подій за деякий період часу. Розподіл Пуассона застосовний для оцінки надійності ремонтованої РЕА з простим потоком відмов.

Вірогідність відсутності відмови за час t складає Р0 = ехр(-lt), а вірогідність появи i відмов за той же час Pi = li ti exp(-lt) /i!, де i = 0, 1, 2 ..., n - число відмов.