Математический эксперимент

Для игрального кубика идеальной формы выпадение чисел от 1 до б будет равновероятным при числе опытов, стремящемся к бесконечности. То же справедливо для идеальной монеты, после подбрасывания она с одинаковой вероятностью Р = 1/2 будет падать на обе стороны (орел или решка). Чтобы убедиться в этом, можно провести эксперимент с большим числом опытов. Результаты такого эксперимента приведены в следующей таблице. Ниже приведен фрагмент таблицы одного из опытов. Всего было выполнено 14 серий опытов (с использованием случайной функции MS Excel).

№ опыта	Орел — 1 Решка — 0	№ опыта	Орел — 1 Решка — 0	№ опыта	Орел — 1 Решка — 0

В следующей таблице приведены результаты обработки результатов 14 серий опытов по 200 бросков в каждой серии. В последнем столбце вычислены среднее количество выпадений орла и решки и их средние вероятности. Действительно, вероятности событий близки — орел выпадал с вероятность 0,51, а решка — 0,49, что согласуется с теоретическими данными.

Орел— 1 Решка —0
№ серии опытов по 200 бросков	Кол-во	Вероятность	Кол-во	Вероятность
		0,44		0,57
		0,59		0,42
		0,53		0,48
		0,55		0,45
		0,56		0,45
		0,47		0,54
		0,49		0,51
		0,48		0,52
		0,55		0,45
		0,51		0,49
		0,54		0,47
		0,48		0,52
		0,51		0,50
		0,53		0,48
Среднее		0,51		0,49

Естественно-научный эксперимент [28]

Пусть проводится эксперимент: последовательно бросают тяжелый шарик с 1, 2, 3, ..., 10 этажа, замеряют высоту начального положения шарика и фиксируют время падения. По результатам эксперимента составляют таблицу. В нее добавляют расчетные значения времени, вычисленные по известной формуле:

Я(м)	из опыта	*(с) расчетное	Среднее абсолютных значений отклонений точек данных от среднего — по функции СРОТКЛ
	0,8	0,78	0,01
	1.1	1,11	0,005
	1,3	1,35	0,025
	1,5	1,56	0,03
	1.7	1,75	0,025
	1.9	1,92	0,01
	2,0	2,07	0,035
	2,2	2,21	0,005
	2,3	2,35	0,025
	2,4	2,47	0,035

где t_{расчетное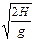} = - зависимость времени падения тела на землю от первоначальной высоты Н без учета сопротивления воздуха, g - ускорение свободного падения.

Для вычисления t_{расчетно}_t в MS Excel была использована функция извлечения квадратного корня из числа — КОРЕНЬ(Х):

=КОРЕНЬ((2*А2/9,81)),где А2 — адрес ячейки, содержащей значение высоты.

Сравнение опытных и расчетных данных таблицы позволяет сделать вывод об адекватности использованной модели зависимости времени падения тела на землю от первоначальной высоты Н без учета сопротивления воздуха. Этот вывод можно сделать, проанализировав отклонение опытных данных от расчетных значений, полученных с помощью встроенной функции «Среднее отклонение» СРОТКЛ, которая возвращает среднее абсолютных значений отклонений точек данных от среднего. СРОТКЛ является мерой разброса множества данных.

<9 10 11 12 131415 >

Дата добавления: 2016-02-16; просмотров: 1561;