В) Специфические нормы.

Специфические нормы. Один из подходов к решению проблемы сопоставимости тестов (согласованию норм) заключается в составлении таблиц эквивалентно­сти показателей разных тестов. Такие таблицы могут быть составлены эквипроцентильным методом, и тогда показатели считаются эквива­лентными, если они имеют равные процентили в данной группе. Другим возможным решением этой проблемы является стандартизация тестов для более узкой популяции, релевантной специфическим целям каждого теста. В таких случаях границы нормативной популяции должны быть четко определены и приведены вместе с нормами. Например, можно указать, что данные нормы относятся к управленческому персоналу крупных производственных фирм или к первокурсникам технических институтов.

Достаточно специализированные нормы желательно иметь для многих целей тестирования. Даже когда имеются репрезентативные нормы для широкой популяции, часто оказываются полезными так называемые подгрупповые нормы. Потребность в них возникает, когда показатели теста заметно меняются от одной подгруппы к другой. Сами подгруппы могут формироваться по признаку возраста, года обучения, типа школьной программы, пола, географического региона, проживания в городе или в сельской местности, социоэкономического уровня и т.д. Именно характер использования теста определяет и наиболее существенный признак формирования подгрупп, и предпочтительность общих или специфических норм.

Следует также упомянуть о локальных нормах, которые нередко раз­рабатываются пользователями тестов для конкретных социальных единиц. Группы, к которым относятся такие нормы, еще более специфичны, чем даже обсуждавшиеся выше подгруппы. Например, предприниматель может выработать нормы, лучше отвечающие специфике предлагаемой работы; администрация университета - нормы, рассчитанные на обучение в данном университете; школа может оценивать выполнение тестов своими учениками в соответствии с собственным распределением показателей. Локальные нормы такого типа в большей степени, чем какие-либо другие, отвечают таким задачам тестирования, как предсказание достижений в труде или учебе, сравнение относительного уровня знаний детей по различным предметам, исследование динамики их развития [1].

Относительность норм.Относительность норм становится очевидна при попытках осуществить сравнения между тестами. Хорошо известно, что независимо от вида показателей тестов, их всегда следует приводить вместе с названием теста, в котором они получены, поскольку тестовые показатели нельзя интерпретировать в отрыве от конкретного теста. Например, если в результате тестирования Иванов получил IQ = 90, а Сидоров - IQ =110, то без последующих разъяснений эти данные ни о чем не говорят. Взаимное положение результатов этих испытуемых может оказаться обратным, если им придется "поменяться" тестами, которые они проходили.

Точно так же относительная позиция индивида по различным психическим функциям может быть неверно истолкована из-за несопоставимости те­стовых норм. Допустим, учащемуся для определения уровня развития некоторых его навыков были даны тесты на понимание слов и пространственное восприятие. Если первый из этих двух тестов стандартизован на случайной выборке учеников старших классов, а второй на группе мальчиков из ремесленного училища, то можно ошибочно заключить, что индивид гораздо более развит в вербальном, чем пространственном отношении, тогда как на самом деле может иметь место обратное.

Существуют три основные причины систематических изменений результатов, полученных одним и тем же индивидом в различных тестах.

Во-первых, тесты, даже если они одинаково называются, могут различаться по содержанию. Примеры тому - тесты интеллекта, обычно фигурирующих под одним и тем же именем. И это, несмотря на то, что одни из них включают в себя только вербальные задания, другие связаны с пространственными навыками, а третьи могут содержать вер­бальные, пространственные и числовые задания.

Во-вторых, могут ока­заться несравнимыми единицы измерения. Например, если IQ одного теста построен при σ =12, а другого, при σ =18, то испы­туемый, который в первом тесте получит IQ= 112, во втором, скорее все­го, будет иметь IQ=118.

В-третьих, характер выборок стандартизации, ис­пользованных при определении норм для разных тестов, может оказаться различным. Очевидно, один и тот же индивид будет выглядеть лучше на фоне более слабой, чем более сильной группы.

Несопоставимость содержания тестов или единиц измерения обычно выявляется при рассмотрении самого теста или руководства по его ис­пользованию. Однако несоответствие нормативных выборок заметить гораздо труд­нее, по всей вероятности, оно и является причиной многих, не поддающихся ино­му объяснению, расхождений в результатах теста.

Обычно показатели конкретного испытуемого сравниваются с нормативными показателями посредством какого-либо преобразования, позволяющего определить место положения этого испытуемого в группе. Рассмотрим некоторые из них.

Процентиль.Прежде, чем рассматривать понятие "процентиля", напомним кратко некоторые свойства нормального распределения. Например, известно [1], что, используя показатель σ(стандартное отклонение)применительно к нормальной кривой распределения, можно представить прямое соответствие между σи относительным количеством случаев (допустим правильных ответов на тест):

Например, для Х = 40 и σ= 4,9 имеем интервал равный + 1σ= 44,9; +2 σ= 49,8. Процент случаев, приходящихся на интервал между Х и +1 σ,для нормального распределения равен 34,13. Так как кривая симметрична, 34,13% случаев приходится также и на интервал от Х до -1σ,таким образом, в диапазоне от -1σ до +1σ приходится 68,26% случаев. Почти все (99,72%) случаи лежат в пределах + 3σ относительно среднего значения.

Различают первичные или "сырые" показатели, которые получаются непосредственно после того, как проведен тест и подсчитаны суммарные баллы, и "производные" показатели – полученные из первичных, "сырых" показателей путем применения к ним каких-либо математических процедур.

В качестве универсальных производных показателей, пригодных для разных (по своей качественной направленности и количеству пунктов) тестов, используется "процентильная мера".

Процентиль - процент испытуемых из выборки стандартизации, которые получили равный или более низкий балл, чем балл данного испытуемого.

Например, если 30% людей правильно решают 5 задач в тесте на пространственное воображение, то первичному показателю 5 соответствует 30-й процентиль (Р30).

Процентили указывают на относительное положение индивида в выборке стандартизации. (Их еще можно рассматривать как ранговые градации, общее число которых равно 100, однако, при ранжировании принято начинать отсчет сверху, т.е. с лучшего члена группы, получающего ранг 1; в то время как, в случае процентилей отсчет ведется снизу, так что чем ниже процентиль, тем хуже позиция индивида).

50-й процентиль (Р50) соответствует медиане. Процентили свыше 50 представляют показатели выше среднего, а те, которые лежат ниже 50, - сравнительно низкие показатели.

25-й и 75-й процентилиизвестны также под названием1-го и 3-го квартилей (Q1 и Q3), поскольку они выделяют нижнюю и верхнюю четверти распределения. Как и медиана, они удобны для описания распределения показателей и сравнения с другими распределениями.

Процентили не следует смешивать с обычными процентными показателями,которые являются первичными показателями и представляют собой процент правильно выполненных заданий, тогда как процентиль - это производный показатель, указывающий на долю от общего числа членов группы.

Процентильные показатели обладают рядом достоинств. Их легко рассчитать и понять даже сравнительно неподготовленному человеку. Их применение достаточно универсально, они одинаково применимы как к детям, так и взрослым и подходят к любому типу теста, измеряет ли он способности или свойства личности.

Процентильные показатели имеют существенные недостатки.Первый - связан с неравенством их как единиц измерения, особенно на краях распределения. Если распределение первичных показателей приближается к нормальной кривой, (что справедливо для большинства тестовых показателей) то различия между первичными показателями вблизи медианы (или центра) распределения в процентильном выражении преувеличены, тогда как аналогичные различия вблизи краев распределения сильно занижены.

Напомним, что в нормальной кривой случаи тесно сгруппированы в центре и по мере приближения к краям рассеиваются. Следовательно, каждый данный процент случаев вблизи центра соответствует более короткому расстоянию по оси абсцисс, чем тот же процент ближе к краям распределения.

На графике 7 это расхождение в промежутках между рангами процентилей хорошо заметно, если, например, сравнить расстояние между Р40 и Р50 с расстоянием между Р10 и P20.

Еще более явно расхождение между этими расстояниями при Р10 и Р1. (В теоретической нормальной кривой нулевой процентиль достигается лишь в бесконечности и поэтому не может быть показан на графике).

То же соотношение получится, если процентили отмечать интервалами одинаковой длины σ, откладывая их влево и вправо от пика нормальной кривой. Такие процентили обозначены в нижней части графика 7. Видно, что разность процентилей между пиком и + 1σ равна 34 (84-50), а между + 1σ и + 2σ - всего 14 (98 - 84).

Второй недостаток: как показатели, процентили нельзя использовать для последующего статистического анализа, поскольку они являются значениями порядковой шкалы.

Итак, процентили показывают относительное положение каждого индивида в нормативной выборке, а не величину различия между результатами.

Стандартные показатели.Преимущественное использование в тестах стандартных показателей объясняется их пригодностью во многих отношениях. Такие показатели выражают отклонение индивидуального результата от средней нормы в единицах, пропорциональных стандартному отклонению распределения [1].

Стандартные показатели могут быть получены как линейным, так и нелинейным преобразованием первичных показателей. Если используется линейное преобразование, то при этом сохраняются соотношения между первичными показателями, поскольку они вычисляются вычитанием из каждого первичного показателя одной и той же величины с последующим делением результата на другую постоянную величину.

Относительная величина разницы между стандартными показателями, полученными при таком линейном преобразовании, в точности соответствует относительной величине различия первичных показателей.

Все свойства первоначального распределения показателей полностью воспроизводятся в распределении стандартных линейных показателей. По этой причине любые вычисления, которые можно производить с исходными данными, могут также выполняться и с линейными стандартными показателями без какого-либо искажения конечных результатов.

Линейно преобразованные стандартные показатели часто именуются просто как стандартный показатель или z - показатель. Чтобы вычислить z, находят разность между индивидуальным первичным результатом и средним значением для нормативной группы и затем делят эту разность на σ нормативной группы.

Очевидно, что получающиеся при таком вычислении отрицательные показатели означают, что выполнение тестов индивидом было ниже среднего. Более того, поскольку для большинства групп область значений умещается в пределах от 3σ ниже и выше среднего значения, удовлетворительное различение индивидуальных показателей возможно, только если zвычисляется с точностью хотя бы до одной десятой. Все это делает показатель z неудобным для вычислений и сообщений результатов.

Поэтому обычно применяется еще одно линейное преобразование, единственная цель которого придать показателям более удобную форму. Стандартное преобразование Z-показателей можно представить в виде формулы:

Z_t = 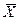+ σZ (**)

где Z_t - преобразованный Z-показатель, 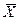– среднее значение преобразованного распределения, σ – стандартное отклонение преобразованного распределения.

Таким образом, чтобы перевести z-показатель в новую шкалу, необходимо просто умножить его на выбранную величину σ, и полученное произведение прибавить (с учетом знака при z) к выбранному среднему значению .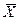

При желании в качестве 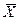и σ можно выбрать любые удобные значения; например, показатели отдельных субтестов в шкалах интеллекта Векслера преобразуются так, что 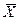=10, а σ=3. Считается (16), что для тестов с распределением баллов, если не полностью нормальным, то более или менее симметричным, преобразованные Z_t -показатели со средним значением 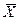= 50 и с σ = 10являются точной значимой нормой.

Все эти меры служат образцами линейного преобразования стандартных показателей.

Напомним, что одной из причин введения производной шкалы вместо первичных показателей является стремление к сопоставимости показателей различных тестов. Значения только что рассмотренных линейно преобразованных стандартных показателей сопоставимы только, если их исходные распределения имеют приблизительно одну и ту же форму.

В этих условиях результат, соответствующий, скажем, +1σ над средним в каких-либо двух тестах, означает, что индивид занимает по отношению к обеим нормативным группам одно и то же положение. Его показатель превышает данные для одного и того же процента членов каждой из групп, и этот процент можно найти из статистических таблиц, если известна форма распределения.

Чтобы добиться сопоставимости результатов, принадлежащих к распределениям различной формы, можно применить нелинейное преобразование, позволяющее придать распределению форму заданной кривой. В качестве эталона обычно используется нормальное распределение, хотя при определенных обстоятельствах другой тип распределения может оказаться более пригодным.

Одним из главных доводов в пользу такого выбора является то, что большинство распределений первичных показателей ближе к нормальному, чем к какому-либо иному. Более того, физические характеристики организма, такие, как рост и вес, измеряющиеся в шкалах с равными единицами, определенными на основе некоторых физических операций, обычно имеют нормальное распределение.

Нормализованные стандартные показатели - это стандартные показатели, соответствующие распределению, преобразованному так, что оно принимает вид нормальной кривой.

Их значения могут быть найдены с помощью таблиц, в которых приводится процент случаев различных отклонений в единицах σ от среднего значения для нормальной кривой. При этом сначала определяется процент лиц в нормативной выборке с тем же или более высоким первичным результатом. Затем этот процент отыскивают в таблице нормального распределения частот и по нему находят соответствующее значение нормализованного стандартного показателя.

Нормализованные стандартные показатели имеют ту же форму, что и линейно преобразованные стандартные показатели, т.е. при среднем значении они равны 0, а при стандартном отклонении равны 1.

Таким образом, значение 0 нормализованный показатель принимает в случае, если индивидуальный результат приходится на самую середину нормальной кривой, т.е. превосходит 50% результатов группы. Результат «-1» означает, что он превосходит приблизительно 16% результатов группы, а «+1» - 84%. Эти проценты соответствуют точкам, лежащим на 1σ ниже и выше среднего значения нормальной кривой (см. график 6).

Как и при линейном преобразовании, нормализованным стандартным показателям можно придать любую удобную форму (используя приведенную выше формулу **).

Например, в руководстве по конструированию психологических тестов (США) считается [8], что типичным преобразованием ненормализованных стандартных показателей должно быть приведение их к распределению со средним значением 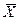= 50 и стандартным отклонением σ = 10. В результате получается T-показатель, предложенный впервые Мак-Коллом: на шкале Т число 50 соответствует среднему значению; 60 показатель в 1σ над средним и т.д.

Таким образом, Т-показатели это нормально распределенные стандартные показатели со стандартным отклонением 10.

Еще одним достаточно известным преобразованием является шкала станайн, разработанная во время второй мировой войны для использования военно-воздушными силами США.

В этой шкале используются только однозначные числа. Среднее значение показателя равно 5, а σ - примерно 2. Название станайн (сокращение от standart nine, т. е. стандартная девятка) связано с тем, что этот показатель принимает значения от 1 до 9. Использование однозначных чисел удобно для машинной обработки, поскольку каждый показатель занимает на перфокарте всего один столбец.

Первичные показатели легко преобразуются в станайны упорядочиванием их числовых значений и приписыванием им новых значений в соответствии с нормальной кривой процентов, приведенной в таблице 3.

Например, если в группе ровно 100 человек, то 4 из них имеющие низшие показатели, получают станайн 1, следующие 7 - станайн 2, следующие 12 - станайн 3 и т. д. Если группа состоит из большего или меньшего числа случаев, то предварительно выясняется, скольким из них соответствует каждый из выписанных в табл. 4 процентов. Так, при 200 случаях станайн 1 будет приписан 8 случаям (4%, 200), а при 150 случаях -6 (4% от 150).

Таблица 3. Проценты нормального распределения для перевода первичных результатов теста в станайны.

Эта таблица была составлена для перевода рядов случаев непосредственно в станайны для любой группы от 10 до 100 случаев. Станайны, ввиду их практических и теоретических достоинств, находят достаточно широкое применение, особенно в тестах способностей и достижений.

Хотя нормализованные стандартные показатели отвечают основным целям тестирования, тем не менее, имеются определенные технические возражения против нормализации всех распределений подряд. Такое преобразование следует проводить при наличии большой и репрезентативной выборки, когда есть основания считать, что отклонение распределения от нормального произошло в силу определенных дефектов теста, а не особенностей выборки или действия других факторов, влияющих на исследуемую функцию. Следует также отметить, что, когда исходное распределение первичных показателей приближается к нормальному, линейные и нормализованные стандартные показатели мало будут отличаться друг от друга. Хотя методы получения этих двух типов показателей совершенно различны, сами показатели в таких условиях будут почти тождественны [1, 15].

В целом, если это возможно, следует предпочесть такую нормализацию распределения, которая достигается надлежащей коррекцией уровней трудности тестовых заданий, а не путем последующего преобразования явно ненормального распределения. При наличии приблизительно нормального распределения первичных показателей линейные стандартные показатели будут служить тем же целям, что и нормализованные стандартные показатели.

Итак,в качестве источника конкретной меры выступает нормативная выборка (выборка стандартизации), на которой построено нормативное распределение тестовых баллов. Как базовые, процентильные шкалы лежат в основе всех традиционных шкал, применяемых в тестологии (T-очки MMPI, баллы IQ, стены 16 PF и др.).

Приведем примеры параметров для наиболее популярных стандартных шкал:

1) Т-шкалаМак-Колла(тест-опросник ММРI и др. тесты, где среднее равно Х = 50, а σ = 10)

2) Шкала IQ: Х=100 и σ =15,

3) Шкала "стэнайнов" (целочисленные значения от 1 до 9 - стандартная девятка): Х=5,0 и σ=2,

4) Шкала "стенов" (стандартная десятка, 16PF Кеттелла) предложена Р.Б. Кеттеллом. Этот способ представляет собой перевод исходных тестовых оценок в 10-балльную шкалу, путем разбиения оси значений тестовых оценок на 10 интервалов, соответствующих долям стандартного отклонения.

Для этого среднее арифметическое по группе принимается за среднюю точку и ей приписывается значение, равное 5,5 балла по стандартной десятибалльной системе. Всякая оценка в интервале ( 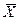+0,25σ)переводится в 6 стенов, а оценка ( 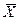-0,25σ)дает стен равный 5.Любое дальнейшее увеличение или уменьшение тестовой оценки на 0,5σувеличивает или уменьшает стандартную оценку на 1 стен.

При такой системе стандартизации к среднему диапазону (или к норме) принято относить стандартные оценки от 4 до 7 стенов. Только при получении стандартных оценок до 3 стенов и выше 8 стенов следует говорить о значимых отклонениях, выходящих за границы средней нормы [13].

Для наглядности приведем образец такой таблицы для фактора "А" - опросника 16PF:

Сырые баллы: 0-4 5-6 7 8-9 10-12 13 14-15 16 17-18 19-20

Стены: 1 2 3 4 5 6 7 8 9 10

Применение стандартных шкал позволяет прибегать на практике к более грубым, приближенным способам проверки типа распределения тестовых баллов. Если, например, процентильная нормализация с переводом в стены и линейная нормализация с переводом в стены по формуле («z») дают совпадающие целые значения стенов для каждого «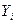 », то это означает, что распределение обладает нормальностью с точностью до «стандартной десятки».

Применение стандартных шкал необходимо для соотнесения результатов по разным тестам, для построения "диагностических профилей" по батарее тестов и тому подобных целей.

Подчеркнем еще раз, что с точки зрения теории измерений процентильные шкалы относятся к порядковым шкалам: они дают информацию, у кого из испытуемых сильнее выражено измеряемое свойство, но ничего не позволяют говорить о том, насколько или во сколько раз сильнее.

Для того, чтобы строить на базе таких шкал количественный прогноз, нужно повысить уровень измерения. Переход к шкалам интервалов производится или на базе эмпирического распределения, или на базе произвольной модели теоретического распределения. В большинстве случаев в роли такой теоретической модели оказывается модель нормального распределения, хотя в общем случае может быть использована любая модель [1, 15].

В дифференциальной психометрике нередко используются еще 2 вида шкал (и соответственно 2 вида тестовых норм):

во-первых, это то, что можно условно назвать "абсолютными тестовыми нормами" - при этом, в роли шкалы выступает сама шкала "сырых" очков;

во-вторых, "критериальные" тестовые нормы, причем, применение таких норм можно считать оправданным в двух случаях:

1) когда сама тестовая "сырая" шкала имеет практический смысл (например, студент, изучающий иностранный язык, должен знать как можно больше слов этого языка, и сырой показатель лексического теста имеет практический смысл);

2) когда применяются "критериальные" тестовые нормы: сырой балл по тесту в результате эмпирических исследований связывается с заданной вероятностью успешности какой-то практической деятельности (например, вероятность успеха "критериальной" деятельности, таковой для упомянутого выше примера может быть синхронный перевод монолога и течение 30 минут).

Контрольные вопросы для самопроверки: §3. Понятие нормы. Проблемы стандартизации показателей.

1. Для чего необходимо рассчитывать тестовые нормы, и какие виды норм существуют?

2. Какие стандартные показатели вы знаете? Перечислите их и дайте краткую характеристику.

3. Чем отличаются линейные стандартные показатели от нелинейных?

4. Что понимается под "нормализованными" стандартными показателями?

5. Какие наиболее распространенные стандартные шкалы Вы знаете? Дайте им краткую содержательную характеристику.

Литература к теме.

1. Анастази А. Психологическое тестирование. В 2-х кн. М., 1982.

2. Бурлачук Л.Ф., Морозов С.М. Словарь-справочник по психодиагностике. - СПб.: Изд-во "Питер", 1999. - 528 с.

3. Общая психодиагностика / Под ред. А. А. Бодалева, В. В. Столина.- М., 1987.

4. Основы психодиагностики / Под ред. А. Г. Шмелева. Ростов-на-Дону., 1996.