Репрезентативность критериальных тестов.

В тестах по критерию в качестве реального эталона применяется критерий (как правило, это какой-то социальный норматив), ради которого создается тест - целевой критерий.

Такая ситуация имеет место в обучении: тестирование, направленное на получение информации об уровне усвоения определенных знаний, умений и навыков (при профессиональном обучении), должно точно отражать уровень освоения этих навыков и тем самым давать надежный прогноз эффективности конкретной профессиональной деятельности.

Рассмотрим операциональную схему шкалирования, применяемую при создании критериального теста [15]. Пусть имеется некоторый критерий С,ради прогнозирования которого психодиагност создает какой-то тест Х.

Для простоты представим С как дихотомическую переменную с двумя значениями - «1» и «0» (например, поступит выпускник школы в вуз или нет). С=1 означает, что i-тый субъект достиг критерия (попал в "высокую" группу по критерию, т.е. поступил в вуз), С =0 означает, что i-тый субъект не достиг критерия (попал в "низкую" группу, т.е. не поступил).

Затем психолог проводит тест Х на интересующей его выборке, и в результате каждый индивид (школьник) получает определенный тестовый балл 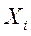. После того как для каждого индивида из выборки становится известным значение С (например, по ступил или нет в вуз), психодиагност располагает всех индивидов по порядку возрастания балла 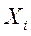и для каждого деления исходной шкалы сырых тестовых баллов подсчитывает с какой вероятностью (Р) каждый индивид (школьник) может попасть в "высокую" группу по критерию.

На графике 8 проиллюстрированы распределения вероятности P(C =1) в зависимости от 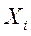. Очевидно, что кривая, представленная на графике 8, является эмпирической линией регрессии С по .

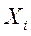Теперь можно сформулировать основное требование к критериальному тесту: линия регрессии должна быть монотонной функцией С от Х. Иными словами, ни для одного более высокого значения 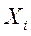вероятность Р не должна быть меньшей, чем для какого-либо менее высокого значения .

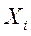Если это условие выполняется, то открывается возможность для критериального шкалирования сырых баллов Х. При критериальном шкалировании к делениям сырой шкалы Х применяется поточечный перевод прямо в шкалу Р на основании эмпирической линии регрессии.

Например, если испытуемый А получил по тесту Х 18 "сырых" очков и этому результату соответствует Р=0,6, то испытуемому А ставится в соответствие показатель 60%.

Конечно, любая эмпирическая кривая является лишь приближенной моделью той зависимости, которая могла бы быть воспроизведена на генеральной совокупности.

Поэтому обычно предпринимаются попытки аппроксимировать эмпирическую линию регрессии какой-либо функциональной зависимостью, что позволяет затем производить прогноз с применением формулы (а не таблицы или графика).

Например, если линия регрессии имеет вид приблизительно такой, какой изображен на рис.6, то применение процентильной нормализации позволяет получить простую линейную регрессию С по нормализованной шкале Z.

Это как раз тот случай, когда имеет место эквивалентность стратегии, использующей выборочно-статистические тестовые нормы, и стратегии, использующей критериальные нормы.

В завершении данного материала, рассмотрим операции по анализу распределения тестовых баллов, построению тестовых норм и проверке их репрезентативности.

Согласно Столину В. В. [15], действия, которые последовательно должен произвести психолог при построении тестовых норм сводятся к такому алгоритму:

1. Сформировать выборку стандартизации (случайную или стратифицированную по какому-либо параметру) из популяции, на которой предполагается применять тест. Провести на каждом испытуемом из выборки тест в сжатые сроки (чтобы устранить иррелевантный разброс, вызванный внешними событиями, происшедшими за время обследования).

2. Произвести группировку "сырых" баллов с учетом выбранного интервала квантования (интервала равнозначности). Интервал определяется величиной W/m, где 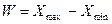- размах; m - количество интервалов шкалы. Необходимо иметь в виду, что группировка индивидуальных баллов, набранных испытуемыми по тесту, сказывается не только на распределении баллов по классам (интервалам квантования), но и на средних показателях, характеризующих то или иное измеряемое свойство. Экспериментальные данные показывают [11], что совершенно не безразлично, не только то, на какое число классов разбивается вся совокупность полученных тестовых баллов, но и как определяются границы первого класса.

Чтобы получились более адекватные результаты обработки статистических данных, рекомендуется:

- во-первых, не брать слишком большой интервал шкалы - он не должен превышать 1/3-1/4 величины среднего квадратичного отклонения;

- во-вторых, определять границы первого класса следует так, чтобы минимальный показатель набранных по тесту баллов, попадал примерно в середину этого класса.

3. Построить распределение частот тестовых баллов в виде таблицы и в виде соответствующих графиков гистограммы и кумуляты.

4. Произвести расчет среднего и стандартного отклонения, а также асимметрии и эксцесса с помощью компьютера. Проверить гипотезы о значимости асимметрии и эксцесса. Сравнить результаты проверки с визуальным анализом кривых распределения.

5. Произвести проверку нормальности одного из распределений (можно с помощью критерия Колмогорова или с одним из указанных способов) или произвести процентильную нормализацию с переводом в стандартную шкалу, а также линейную стандартизацию и сравнить их результаты (с точностью до целых значений стандартных очков).

6. Если совпадения не будет - нормальность отвергается, тогда произвести проверку устойчивости распределения расщеплением выборки на две случайные половины. При совпадении нормализованных баллов для половины и для целой выборки считать нормализованную шкалу устойчивой.

7. Проверить однородность распределения по отношению к варьированию заданного популяционного признака (пол, профессия и т.п.) с помощью критерия Колмогорова. Построить графики гистограммы и кумуляты для полной и частной выборок. При значимых различиях разбить выборку на разнородные подвыборки.

8. Построить таблицы процентильных и нормализованных тестовых норм (для каждого интервала шкалы "сырого" балла). При наличии разнородных подвыборок для каждой подвыборки должна быть своя таблица.

9. Обсудить конфигурацию полученных распределений.

10. В случае негативных результатов - отсутствия устойчивых норм для шкалы с заданным числом интервалов - осуществить обследование более широкой выборки или отказаться от плана использования данного теста.

Контрольные вопросы для самопроверки: §4, 5. Подсчет параметров и оценка типа распределения.

1.Что понимается под понятием "репрезентативности"?

2. Для чего необходима проверка устойчивости распределения?

3. На чем основана общая логика проверки устойчивости распределения тестовых баллов?

4. Как проверяется репрезентативность критериальных тестов?

5. Какие действия последовательно должен произвести психолог при построении тестовых норм?

Литература к теме.

1. Анастази А. Психологическое тестирование. В 2-х кн. М., 1982.

2. Бурлачук Л.Ф., Морозов С.М. Словарь-справочник по психодиагностике. - СПб.: Изд-во "Питер", 1999. - 528 с.

3. Гусев А. Н., Измайлов Ч. А., Михалевская М. Б. Измерение в психологии: общий психологический практикум. М.: Смысл, 1997. -287 с.

4. Дружинин В.Н. Экспериментальная психология: Учебное пособие - М.: ИНФРА-М, 1997. - 256 с.

5. Общая психодиагностика / Под ред. А. А. Бодалева, В. В. Столина.- М., 1987.

6. Основы психодиагностики / Под ред. А. Г. Шмелева. Ростов-на-Дону., 1996.