Методы приведения к четкости.

1. Дефаззификация – приведение к четкости (defuzzification). Преобразование нечеткого набора выводов в число.

Алгоритмы нечеткого вывода Мамдани (Mamdani).

Пусть заданы два нечетких правила:

П₁: если х есть А₁ и y есть В₁, тогдаzесть С₁, П₂: если х есть А₂ и y есть В₂, тогдаz есть С₂.

1) Нечеткость. Находят степени принадлежности для предпосылок каждого правила: А₁(х₀), А₂(х₀), B₁(y₀), B₂(y₀).

2) Нечеткий вывод. Определяют уровни «отсечения» для предпосылок каждого правила (операция min):

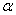₁= А₁(х₀) 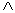B₁(y₀), 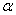₂= А₂(х₀) 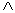B₂(y₀).

определяют усеченные функции принадлежности

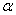С'₁=( ₁ 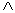С₁(z)), С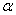'₂=( ₂ 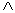С₂(z)).

3) Композиция. Производится объединение найденных усеченных функций (операция max), получают нечеткое подмножество для переменной выхода с функцией принадлежности:

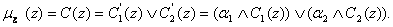
(5.16)

4) Дефаззификация. Приведение к четкости (определение z₀), например, центроидным методом (как центр тяжести для кривой ):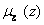

.

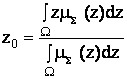(5.17)

Алгоритм иллюстрируется на рисунке 5.2.

Алгоритмы нечеткого вывода Сугено (Sugeno) и Такаги (Takagi).

Сугено (Sugeno) и Такаги (Takagi) использовали набор правил в следующей форме:

П₁: если х есть А₁ и y есть В₁, тогда z=a₁x+b₁y, П₂: если х есть А₂ и y есть В₂, тогдаz =a₂x+b₂y.

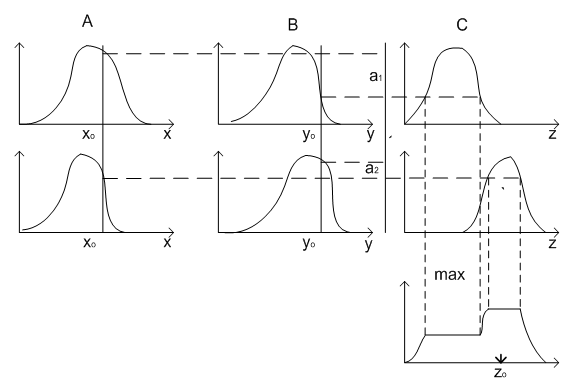
Рисунок 5.2 – Графическая интерпретация алгоритма Мамдани