Общая структура нечеткого микроконтроллера

Структура блока нечеткой логики.

Наиболее важным применением теории нечетких множеств являются контроллеры нечеткой логики. Их функционирование несколько отличается от работы обычных контроллеров; для описания системы вместо дифференционных уравнений используются знания экспертов. Эти знания могут быть выражены с помощью лингвистических переменных, которые описаны нечеткими множествами.

Общая структура нечеткого микроконтроллера

Общая структура микроконтроллера, использующего нечеткую логику, показана на рис.1. Она содержит:

• блок фаззификации;
• базу знаний;
• блок решений;
• блок дефаззификации.

Блок фаззификации преобразует четкие величины, измеренные на выходе объекта управления, в нечеткие величины, которые описаны лингвистическими переменными в базе знаний.

Блок решений использует нечеткие условные ( if - then ) правила, заложенные в базу знаний, для преобразования нечетких входных данных в необходимые управляющие влияния, которые также носят нечеткий характер.

Блок дефаззификации превращает нечеткие данные с выхода блока решений в четкую величину, которая используется для управления объектом.

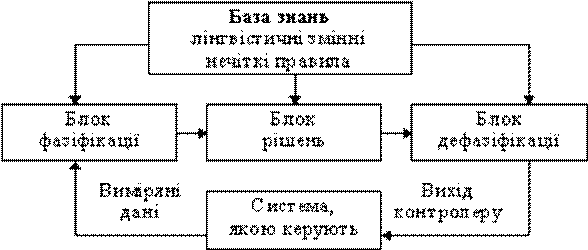
Рис. 1. Общая структура нечеткого микроконтроллера

В качестве примера известных микроконтроллеров, использующих нечеткую логику можно назвать 68HC11, 68HC12 фирмы Motorola, MCS-96 фирмы Intel, а также некоторые другие.

Все системы с нечеткой логикой функционируют по одному принципу: показания измерительных приборов: фаззифицируются (превращаются в нечеткий формат), обрабатываются, дефаззифицируются и в виде обычных сигналов подаются на исполнительные устройства.

Рассмотрим случай управления мобильным роботом, задачей которого является объезд препятствий. Введем две лингвистические переменные: ДИСТАНЦИЯ (расстояние от робота до препятствия) и НАПРАВЛЕНИЕ (угол между продольной осью робота и направлением к препятствию).

Рассмотрим лингвистическую переменную ДИСТАНЦИЯ. Ее значения можно определить термами ДАЛЕКО, СРЕДНЕ, БЛИЗКО и ОЧЕНЬ БЛИЗКО. Для физической реализации лингвистической переменной необходимо определить точные физические значения термов этой переменной. Пусть переменная ДИСТАНЦИЯ может принимать любые значения из диапазона от нуля до бесконечности. Согласно теории нечетких множеств, в таком случае каждому значению расстояния из указанного диапазона может быть поставлено в соответствие некоторое число от нуля до единицы, которая определяет степень принадлежности данного физического расстояния (допустим 40 см) до того или другого терма лингвистической переменной ДИСТАНЦИЯ. Степень принадлежности определяем функцией принадлежности М(d), где d - расстояние до препятствия. В нашем случае расстояние 40 см. Можно задать степень принадлежности до терма ОЧЕНЬ БЛИЗКО равное 0,7 , а до терма БЛИЗКО - 0,3 (рис. 2.). Конкретное определение степени принадлежности проходит только при работе с экспертами.

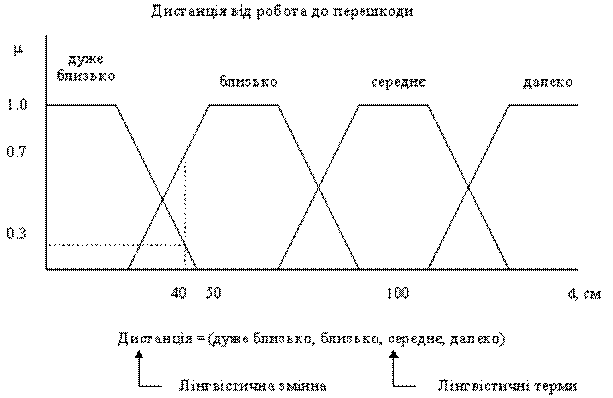
Рис. 2. Лингвистическая переменная и функция принадлежности

Переменной НАПРАВЛЕНИЕ, которая принимает значения в диапазоне от 0 до 360 градусов, зададим термы ЛЕВЫЙ, ПРЯМОЙ и ПРАВЫЙ.

Теперь необходимо задать исходные переменные. В данном примере достаточно одной, которую назовем РУЛЕВОЙ УГОЛ. Она может содержать термы: РЕЗКО ВЛЕВО, ВЛЕВО, ПРЯМО, ВПРАВО, РЕЗКО ВПРАВО. Связь между входом и выходом запоминается в таблице нечетких правил.

Каждая запись в данной таблице соответствует своему нечеткому правилу, например "Если дистанция близко и направление правое , тогда рулевой угол резко влево".

Таким образом, мобильный робот с нечеткой логикой будет работать по следующему принципу: данные от сенсоров про расстояние до препятствия и направление к нему будут фаззифицированы, обработаны согласно табличным правилам, дефаззифицированы, и полученные данные, в виде управляющих сигналов поступают на приводы робота.