Связь скорости течения в реках и каналах с характеристиками русла

Выделим в потоке столб воды высотой Н, равной глубине потока, и сечением 1 м². От угла наклона дна реки (канала) зависит величина составляющей силы тяжести, направленной параллельно водной поверхности. Пусть a – угол наклона дна по отношению к горизонтальной плоскости, а G – сила тяжести столба воды высотой Н и сечением 1 м² (рис.3.25).

Тогда искомая составляющая силы тяжести G_x(«движущая» сила) равна G_x= G×sina, где sina= i – уклон дна. Из рис. 3.25 следует, что sina= G_x/G. Следовательно, движущая сила пропорциональна уклону G_x= G×i . Объем рассматриваемого столба воды равен произведению высоты (Н) на площадь сечения (1 м²), тогда его вес равен G=r×g×Н (g – ускорение силы тяжести, r– плотность жидкости). Таким образом, G_x= G×i =r×g×Н×i, т.е. движущая сила пропорциональна глубине потока и уклону. На рис. 3.25 сила G_x уравновешивается силой сопротивления Т. В курсах гидравлики показано, что сила сопротивления при турбулентном движении жидкости пропорциональна квадрату скорости течения, откуда следует широко известная в инженерной практике формула Шези для расчета скорости течения v:

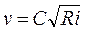
(3.34)

где С – скоростной коэффициент, который определяется по формуле Маннинга

С =(Н^1/6)/n, (3.35)

n – коэффициент шероховатости, определяемый по таблицам в зависимости от состояния дна и стенок потока (ручей, река, канал, труба и др.).

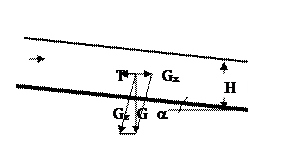
Рис. 3.25. Силы, действующие при движении столба воды высотой Н (обозначения в тексте).

Коэффициент шероховатости речного русла n находят по спе­циальным таблицам. Например, для ровных незаросших русел с песчаным дном n = 0,020 – 0,023; для извилистых русел с неров­ным дном n = 0,023-0,033; для пойм, заросших кустарником, n = 0,043-0,55 и т.д.

Согласно формуле Шези, скорость течения в речном потоке тем больше, чем больше глубина русла и уклон водной поверхности и меньше шероховатость русла. При заданном расходе воды, увеличение шероховатости русла в результате образования ледяного покрова или зарастания дна и берегов водной рас­тительностью, приводит к увеличению глубины (и повыше­нию уровня воды). Следовательно, зимой на реках, покрытых льдом, уро­вень воды обычно выше, чем летом при тех же расходах воды. В условиях теплого климата в период бурного развития растительности в руслах рек уровень воды также повышается.

Движение паводка

Паводки (паводочные вол­ны) при движении вдоль речного русла трансформируются. Это проявляется в их распластывании, т.е. в уменьшении высоты и возрастании продолжительности паводка, в изменении фор­мы паводочной волны (рис. 3.26). Паводки перемещаются подобно распространению волн на воде – гребень волны перемещается быстрее ее подошвы. Уклоны, и, следовательно, скорости течения, в лобовой части паводочной волны больше, чем в тыловой, что приводит к растягиванию (распластыванию) волны паводка. Этому способствует и выход воды на пойму, где, из-за большей шероховатости движение воды замедляется, и значительные массы воды заполняют емкость поймы. Скорость перемещения гребня паводочной волны при отсутствии поймы обычно больше средней скорости течения воды в 1,2–1,5 раза.

При перемещении в реках волн половодья или паводка изменение глубины или уровня воды (Н), расхода воды (Q), средней скорости те­чения (v), уклона водной поверхности (i) происходит несинхронно. Выполненный М.А. Великановым [7] математический анализ движения паводка показал, что в любом створе реки должна наблюдаться следующая последовательность наступле­ния максимальных значений перечисленных характеристик: снача­ла своего максимума достигает уклон, затем скорость течения, потом наступает максимальное значение расхода воды и лишь после всего максимальной величины достигает уровень воды (пик паводка). Как известно из курса гидрометрии, не одновременное наступление максимальных значений расхода и уровня воды во время паводка или половодья предопределяет неоднозначность «кривой расходов»; на графике Q=f(H) появляет­ся поводочная петля (см. рис. 3.27).

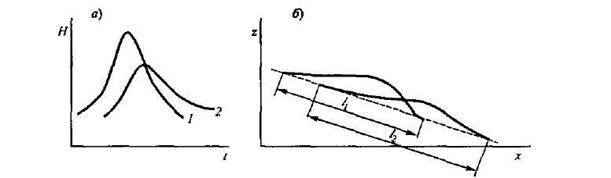
Рис 3.26. Схема трансформации паводочной волны (по М. А Великанову): а–графики изменения уровня воды в двух пунктах, расположенных последовательно вдоль русла (1 и 2), б–продольные профили паводочной волны и се длины в два последовательных момента времени.