Тема 5 Средние величины и показатели вариации

5.1 Понятие о средних величинах, условия их применения

5.2 Виды средних и способы их вычисления

5.2.1 Степенные средние

5.2.2 Структурные средние

5.3 Показатели вариации

5.4 Использование показателей вариации в анализе взаимосвязей

1. Понятие о средних величинах, условия их применения

Среди обобщающих показателей, которыми статистика характеризует изучаемые явления, одно из центральных мест занимают средние величины. Это объясняется тем, что статистика изучает совокупности по варьирующим (изменяющимся, колеблющимся) признакам, причем вариация проявляется в изменении количественных значений признака у отдельных единиц совокупности. Например, отличаются по отдельным работникам предприятия такие признаки как заработная плата, стаж работы, возраст, производительность труда и т.д. В этих условиях для получения обобщающей характеристики совокупности рабочих по названным признакам рассчитывают среднюю их величину.

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.

Вычисление среднего – один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. Средняя величина всегда обобщает количественную вариацию признака, т. е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами.

Средняя – это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает. Для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц - это является основным условием научно обоснованного использования средних.

Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления, фальсифицировать его, или будут бессмысленными. Так, если рассчитать средний уровень доходов взрослого населения какого-либо региона, то получится фиктивный средний показатель, поскольку для его исчисления использована неоднородная совокупность, включающая в себя пенсионеров, работников предприятий различных отраслей и сфер экономики, в которых уровень оплаты труда имеет существенные различия (промышленности, сельского хозяйства, строительства, образования, культуры, здравоохранения и др.). В таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и исчисляются типические групповые средние.

Вместе с тем при проведении макроэкономического анализа (на уровне государства или единой экономической системы) нельзя ограничиваться применением средних только для характеристики значений признаков в однородных по данному признаку совокупностях. В этом случае статистика использует так называемые системные средние, обобщающие неоднородные явления, например, средний валовой внутренний продукт государства на душу населения, средняя заработная плата занятых в экономике, средний реальный доход на душу населения, производительность общественного труда и т.п.

Каждая средняя характеризует изучаемую совокупность по какому-либо одному признаку, но для полной характеристики любой совокупности, описания ее типических черт и качественных особенностей нужна система средних показателей. Поэтому в практике отечественной статистики для изучения социально-экономических явлений и их полной характеристики, как правило, исчисляется система средних показателей. Так, например, показатели средней заработной платы оцениваются совместно с показателями средней выработки, фондовооруженности и энерговооруженности труда, степенью механизации и автоматизации работ и др.

Средняя должна вычисляться с учетом экономического содержания исследуемого показателя. Поэтому для конкретного показателя, используемого в социально-экономическом анализе, можно исчислить только одно истинное значение средней на базе научного способа расчета.

5.2 Виды средних и способы их вычисления

Выбор вида средней величины определяется экономическим содержанием определенного показателя и исходных данных. В статистическом анализе используются два класса средних величин: степенные средние и структурные средние.

5.2.1 Степенные средние

К классу степенных средних величин относятся: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя кубическая.

Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной. Простая средняя считается по несгруппированным данным и имеет следующий общий вид:

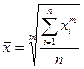(5.1)

где x_i – варианта (значение) осредняемого признака; m - показатель степени средней; n – число вариант.

Взвешенная средняя считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения:

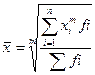(5.2)

где x_i – варианта (значение) осредняемого признака или среднее значение интервала, в котором измеряется варианта; m - показатель степени средней; – f_i частота, показывающая, сколько раз встречается i – e значение осредняемого признака.

В зависимости от значения показателя степени m различают следующие виды степенных средних:

при m = -1 — средняя гармоническая ;

при m = 0 — средняя геометрическая ;

при m = 1 — средняя арифметическая ;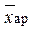

при m = 2 — средняя квадратическая ;

при m = 3 — средняя кубическая .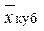

При использовании одних и тех же исходных данных, чем больше m в формулах 5.1 и 5.2, тем больше значение средней величины:

(5.3)

Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется в статистике правилом мажорантности средних.

Характер имеющихся данных определяет существование только одного истинного среднего значения показателя. Вид средней выбирается в каждом отдельном случае путем конкретного анализа изучаемой совокупности, он определяется материальным содержанием изучаемого явления, а также принципами суммирования и взвешивания.

Остановимся подробнее на степенных средних.