Абсолютная разрешающая способность

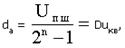
где U_пш - напряжение полной шкалы, соответствующее опорному напряжению ЦАП. Это напряжение можно считать равным максимальному выходному напряжению; 2ⁿ - 1 = N - количество ступеней квантования.

Численно абсолютная разрешающая способность равна шагу квантования Du_кв.

3. Абсолютная погрешность преобразования d_пш показывает максимальное отклонение выходного напряжения U_вых в точке пересечения с идеальной характеристикой (прямой) на уровне напряжения полной шкалы (рис. 2). Абсолютная погрешность преобразования оценивается в процентах или же в единицах младшего значащего разряда (МР). При оценке значения абсолютной погрешности преобразования знак напряжения не учитывается.

4. Нелинейность преобразования ЦАП d_лн определяет максимальное отклонение реальной характеристики от идеальной (рис. 5) и оценивается также в процентах или в единицах младшего значащего разряда.

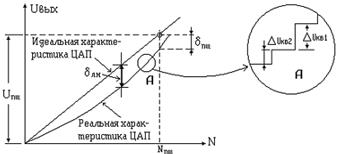
Рисунок 5 Пояснения к определению погрешностей преобразования ЦАП

5. Дифференциальная нелинейность преобразования ЦАП d_дф.лн численно равна максимальной разности двух соседних приращений (шагов квантования)

d_дф.лн = Du_{кв 1} - Du_кв2.

Дифференциальная нелинейность оценивается в младших значащих разрядах и обычно не превышает нескольких единиц мр.

Младший значащий разряд численно определяет минимальное значение выходного напряжения, т.е. квант напряжения. Для оценки дифференциальной нелинейности d_дф.лн в процентах можно воспользоваться выражением

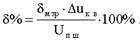
Время установления выходного напряжения или тока t_уст - интервал времени от подачи входного двоичного входного кода до вхождения выходного сигнала в заданные пределы. Максимальная частота преобразования f_пр - наибольшая частота дискретизации, при которой параметры ЦАП соответствуют заданным значениям. Максимальная частота и время установления определяют быстродействие ЦАП.

Виды ЦАП условно можно разделить на две группы: с резисторными матрицами, безматричные ЦАП. В интегральном исполнении применяются только ЦАП с прецизионными резисторными матрицами, формирующими выходные сигналы путем суммирования токов.

ЦАП содержит элементы цифровой и аналоговой схемотехники. В качестве аналоговых элементов используются операционные усилители, аналоговые ключи (коммутаторы), резисторные матрицы и т.д.

Аналоговые элементы, входящие в состав ЦАП, практически полностью определяют его качественные и эксплуатационные параметры, основную роль при этом играют точность подбора номиналов резисторов резисторной матрицы и параметров операционного усилителя (ОУ).

При построении ЦАП и АЦП применяются аналоговые ключи, коммутирующие цепи аналоговых сигналов под воздействием управляющих цифровых сигналов. Токи, коммутируемые электронными аналоговыми ключами, не превышают 10 - 50 мА. Относительно высокое сопротивление открытого ключа (50 - 600 Ом) требует наличия высокоомной нагрузки, что обеспечивается высокоомным входным сопротивлением ОУ.

При реализации ЦАП в интегральном исполнении большие трудности вызывает подгонка высокоточных резисторов с сопротивлениями, отличающимися по номиналам друг от друга на несколько порядков. Поэтому, в интегральном исполнении применяются исключительно резистивная матрица R - 2R. В качестве примера рассмотрим четырехразрядный ЦАП, использующий схему суммирования токов на ОУ (рис. 6).

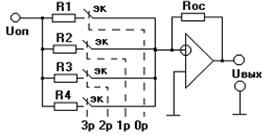
Рисунок 6 Схема простейшего ЦАП

Относительная разрешающая способность рассматриваемого ЦАП:

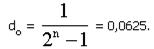
Абсолютная разрешающая способность определяется при известном значении опорного напряжения U_оп. Наиболее удобными значениями U_оп являются напряжения, кратные степени двойки, т.е. 10,24 В, 5,12 В, 2,56 В и т.д.

Если принять значение опорного напряжения равным 10,24 В, то абсолютная разрешающая способность (DU_кв) определяется как:

DU_кв = 0,0625 × 10,24 = 0,625В.

Сопротивление резистора в цепи ключа, управляемого старшим разрядом двоичного кода, должно быть в два раза больше сопротивления резистора обратной связи R_ос. Сопротивление каждого последующего младшего разряда в два раза больше, чем сопротивление соседнего старшего разряда. Отсюда следует, что с увеличением количества разрядов цифровых входов ЦАП резко увеличивается соотношение сопротивлений резисторов нулевого и самого старшего разрядов (R₀=2ⁿR_n):

R₀/R_n = 2ⁿ = T.

Если n = 8, то это отношение составляет 256. Увеличение Т может привести к чрезмерному увеличению сопротивления резистора младшего разряда или же к сильному уменьшению номинала резистора самого старшего разряда. Поэтому ЦАП с резистивной матрицей R - 2ⁿR применяется при небольшом количестве разрядов (при n < 8). При больших Т затруднительным становится также изготовление резистивных матриц в интегральном исполнении. Известно, что номиналы резисторов в интегральном исполнении не должны превышать 50...100 кОм. Поэтому, в ЦАП, выполненных по интегральной технологии, в основном применяются резистивные матрицы R-2R. Функциональная схема ЦАП с матрицей R-2R показана на рис. 7.

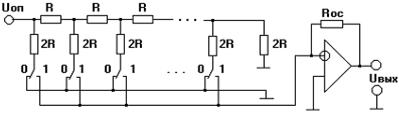
Рисунок 7 ЦАП с резистивной матрицей R - 2R

Напряжение на выходе ЦАП (рис. 6) определяется как:

Чтобы выполнить условие формирования выходного напряжения в соответствии с двоичным кодом входного числа, необходимо получить равенство R_ос=R, тогда

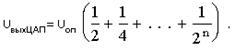
Дробные члены суммы играют роль весовых коэффициентов, а шаг квантования определяется отношением DU_кв = U_оп/2n. На рис. 7 символы “0” и “1” перед электронными ключами показывают на состояние ключа при подаче на цифровые входы ЦАП логического “0” или “1”, соответственно.

ЛИТЕРАТУРА

Основная

1. Касаткин В.С., Немцов М.В., Электротехника. - М.; Энергоатомиздат, 2000.

2. Основы промышленной электроники /Под ред. В.Г. Герасимова.- М.: Высшая школа, 1985.

3. Основы теории цепей; Учебник для ВУЗов. /В.П.Бакалов и др. 2-ое изд. перераб. и доп. – М.; 2000.

4. Сборник задач по электротехнике и основам электроники / Под ред. В.Г. Герасимова.- М.: Высшая школа, 1987.

5. Прянишников В.А. Электроника. - СПб; Корона принт, 2002.

6. Хоровиц П., Хилл У.. Искусство схемотехники.- М.:Мир, 1997.

7. Амочаева Г.Г. Электронный конспект лекций.

Дополнительная

1. Алексеенко А.Г., Шагурин Н.И. Микросхемотехника. Учебное пособие для вузов.- М.: Радио и связь, 1990.

2. Жеребцов И.П. Основы электроники.- Л.: Энергоатомиздат, 1990.

3. Попов В.П., Основы теории цепей.- Учебник для ВУЗов.- 3-е изд. испр.-М.: Высшая школа, 2000.

4. Электротехника и электроника в экспериментах и упражнениях: Практикум на Electronics Workbench. в 2-х томах, Под ред. Д.И. Панфилова ДОДЭКА, 1999.-т.1-Электроника.

5. Электротехника/Ю.М. Борисов, Д.Н. Липатов, Ю.Н. Зорин. Учебник для вузов.- 2-е изд., перераб. и доп.- М.: Энергоатомиздат, 1985.

Лекция №20