Динамические свойства преобразователей

При выборе преобразователей для измерения переменных во времени величин (давление, ускорение и т.п.) нужно по­мнить о погрешностях, связанных с динамическим режимом работы преобразователей и обусловленных инерцией преоб­разователей.

В общем случае устройство подобных преобразователей может быть представлено моделью согласно рис. 3.6.

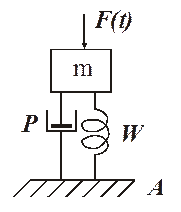
Рис. 3.6. Модель преобразователя.

Здесь F(t) —внешняя переменная сила, которая действует на массу m, связанную с неподвижным телом А упругим эле­ментом (например, пружиной W)', Р—демпфер (успокои­тель).

Приведите примеры.

Рис. 3.7

Рис. 3.8

Рис. 3.9

Рис. 3.10

В преобразователях такого вида могут быть погрешности двух типов: амплитудная и фазовая.

Амплитудная погрешность

Если к массе m приложена переменная сила F, то при ее воздействии амплитуда колебаний массы m оказывается боль­ше по сравнению с амплитудой перемещения ее при единич­ном воздействии силы.

Исследования уравнения движения подвижной части пре­образователей в динамическом режиме при синусоидальном законе изменения силы во времени дали кривые зависимости D=f(l), изображенные на рис. 3.11.

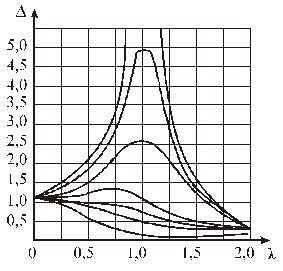
Рис. 3.11. Амплитудная погрешность преобразователей.

Здесь D-отклонение наибольшей амплитуды колебаний в динамическом режиме (вынужденные колебания) к амплитуде перемещения под­вижной части при единичном воздействии силы - есть ампли­тудная погрешность вынужденных колебаний, равная:

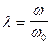- отношение угловой частоты вынужденных ко­лебаний к частоте w₀ собственных колебаний подвижной части; b - степень успокоения подвижной части;

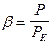(P_K - коэффициент успокоения при критическом ре­жиме движения массы, т. е. при наименьшем времени успокоения).

Как видно из кривых на рис. 3.13, при малых значениях b максимальная амплитудная погрешность имеет место при l=1, т.е. при резонансе (w=w₀). Поэтому преобразовате­ли перемещений и сил, работающие в динамическом режиме, должны иметь 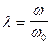много меньше единицы, т.е. должны иметь собственную частоту w₀ больше частоты измеряемого процесса w.

Нельзя иметь отношение 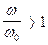, так как если собственная частота преобразователя w₀ будет меньше частоты из­меряемого процесса w, деталь (масса т) может выходить из соприкосновения с силой F и измерения будут неверные. Из кривых на рис. 3.13 видно, что амплитудная погрешность D за­висит также от степени успокоения подвижной части преоб­разователя и имеет наименьшее значение при b = 0,6—0,4.

Фазовая погрешность

Фазовая погрешность выражается в запаздывании вынуж­денных колебаний подвижной части от колебаний измеряемой величины.

Эта погрешность имеет вид, изображенный на рис. 3.14. Здесь y-фазовая погрешность.

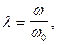
Из рис. 3.12 видно, что при b=0,7 изменение фазовой по­грешности имеет почти линейную зависимость от l, а также - что y меньше при малом l

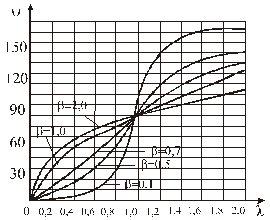
Рис. 3.12. Фазовая погрешность преобразователей.

При синусоидальном колебании подвижной части ампли­тудная погрешность может быть вычислена по следующей формуле:

,

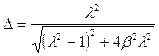а фазовая погрешность

.

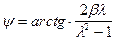Из всего сказанного можно сделать следующий вывод: при измерении переменных во времени механических величин во избежание больших амплитудных и фазовых погрешностей важно так подобрать параметры преобразователя, чтобы обес­печить соответствующее соотношение частоты собственных ко­лебаний преобразователя и частоты измеряемого процесса (вынужденных колебаний), а также степень успокоения под­вижной части преобразователя b=0,6—0,4.