АРИФМЕТИЧЕСКИЕ ОСНОВЫ ЦИФРОВОЙ ТЕХНИКИ 5 страница

Выходы элементов с открытым коллектором (стоком) можно соединять параллельно, подключая их к общему резистору (рисунок 20, а).

При этом можно получить режим поочередной работы элементов на общую линию, как и для элементов с тремя состояниями выхода, если активным будет лишь один элемент, а выходные транзисторы всех остальных элементов будут заперты. Если же разрешить активную работу всех элементов, выходы которых соединены, то можно получить дополнительную логическую операцию монтажной логики (монтажное И) над выходными сигналами логических элементов (рисунок 20, а).

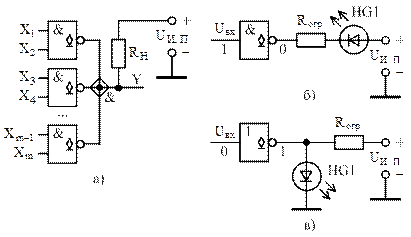
Рисунок 20 – Схема реализации монтажной логики (а) и индикации уровня логической единицы (б) и уровня логического нуля (в) с помощью логических элементов с открытым коллектором (стоком)

При реализации монтажной логики высокий уровень 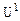на общем выходе Y возникает только при запирании выходных транзисторов всех логических элементах, так как насыщение хотя бы одного из них снижает выходное напряжение до уровня

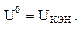Поскольку каждый элемент выполняет операцию

И-НЕ над своими входными аргументами, общий результат окажется следующим:

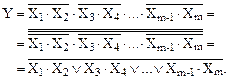(33)

Таким образом, над входными аргументами выполняется логическая операция И-ИЛИ-НЕ.

В УГО элементов с открытым коллектором (стоком) ставится ромб с черточкой снизу (рисунок 20).

На рисунке 20, б и 20, в показана схема индикации уровня логической единицы и нуля соответственно с помощью светодиодного индикатора HG1. Роль ключевого элемента выполняет инвертор с открытым коллектором (стоком). В первой схеме замыкается цепь для прямого тока светодиода и диод зажигается, если выходной транзистор инвертора открыт (на входе схемы уровень логической единицы), а во второй – наоборот, если выходной транзистор закрыт (на входе схемы уровень логического нуля).

В схеме на рисунке 20, б через светодиод будет протекать ток 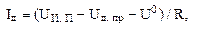следовательно, для
его задания требуется выполнение условия 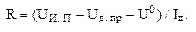В этом случае требуется управляющий элемент с достаточно большим выходным током в нулевом состоянии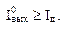

В схеме на рисунке 20, в через светодиод проте-
кает ток 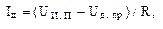откуда следует 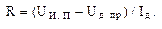Выходной ток управляющего элемента должен удовлетворять условию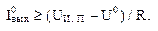

Достоинством элементов с открытым коллектором (стоком) при работе в магистрально-модульных системах является их защищенность от повреждений из-за ошибок управления, приводящих к одновременной выдаче на общую шину нескольких слов, а также возможность реализации дополнительных логических операций монтажной логики.

Недостатком таких элементов является большая задержка переключения из состояния логического 0 в состояние логической 1 из-за медленного заряда выходной емкости малым током резистора R.

Во многих современных ИС используются выходные каскады с возможностью их программирования на работу в одном из двух вариантов: либо как каскада с открытым коллектором (стоком), либо как каскада с третьим состоянием [4].

Построение узлов цифровых устройств на стандартных микросхемах

Разработанная схема цифрового устройства может содержать логические элементы с разным числом входов. Иногда необходимо использовать в схеме логические элементы, число входов которых больше или меньше выпускаемых промышленностью. Рассмотрим возникающие в этих случаях особенности построения цифровых устройств.

Избыточный вход мог бы быть оставлен свободным, т.е. не подключенным к каким-либо цепям. Однако для уменьшения влияния наводимых на этот вход помех нежелательно неиспользуемый вход оставлять свободным. Для элементов схемотехники КМОП это строгая рекомендация. При этом возможны следующие способы его включения. Неиспользуемый вход может быть подключен к любому из используемых входов. Недостатком такого способа является увеличение нагрузки на источник сигнала, что увеличивает задержку распространения сигнала, т.е. снижает быстродействие элемента. Поэтому наиболее удачным следует считать способ, при котором на неиспользуемый вход подается константа нуля или единицы, не изменяющая работу элемента для используемых входов. Причем на свободные входы элементов ИЛИ и ИЛИ-НЕ подается уровень логического нуля (вход соединяется с корпусом устройства), а для элементов И и И‑НЕ – уровень логической единицы (вход соединяется с источником питания через резистор сопротивлением несколько килоом).

Логические элементы ИЛИ-НЕ и И-НЕ, в которых используется лишь один вход, а остальные соединены способом, описанным выше, выполняют операцию НЕ.

Наращивание числа входов для логических элементов И и ИЛИ не представляет трудностей, так как для получения нужного числа входов берется несколько элементов, выходы которых объединяются далее элементом того же типа (рисунок 21).

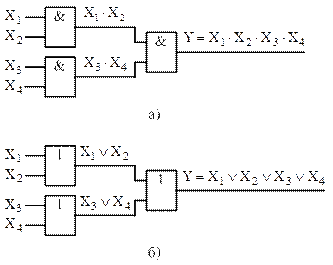
Рисунок 21 – Схема наращивания числа входов для логических элементов И (а) и ИЛИ (б)

Наращивание числа входов для логических элементов И-НЕ, ИЛИ-НЕ производится аналогичным способом, но в схеме появляются дополнительные инверторы (рисунок 22).

Очевидным недостатком рассмотренного метода наращивания числа входов является снижение быстродействия, что особенно проявляется в схеме на рисунке 22.

Режимы неиспользуемых элементов. Если не все элементы, имеющиеся в корпусе ИС, использованы, то следует помнить, что неиспользованные элементы также подключены к источнику питания, которое является общим для всего корпуса. Если же мощности, потребляемые элементами в состояниях нуля и единицы, не равны, то неиспользуемый элемент следует поставить в состояние минимальной мощности, подав на какой-либо из его входов соответствующую константу.

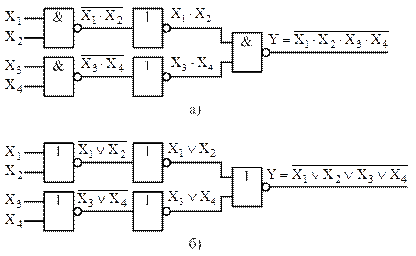
Рисунок 22 – Схема наращивания числа входов для логических элементов И-НЕ (а) и ИЛИ-НЕ (б)

Снижение нагрузок на выходах логических элементов может понадобиться, если нагрузки превышают допустимые значения, а также для повышения быстродействия схем, на которое нагрузки элементов оказывают самое непосредственное влияние. Чем больше у элемента-источника сигнала число нагрузок, тем большее время тратится на достижение выходным сигналом порогового уровня при переключении. Для предотвращения потерь быстродействия из-за нагрузок на выходах сильно нагруженных элементов применяют буферизацию или разделение нагрузки (рисунок 23).

Введение буферных каскадов ускоряет работу источника сигнала, но вносит собственную задержку в тракт передачи. Будет ли в конечном счете эффект ускорения, определяется конкретным расчетом.

При разделении нагрузки новые задержки в тракт передачи сигнала не вводятся, но увеличивается нагрузка на тот источник сигнала, который питает рассматриваемую схему, поэтому и здесь эффективность должна оцениваться конкретным расчетом.

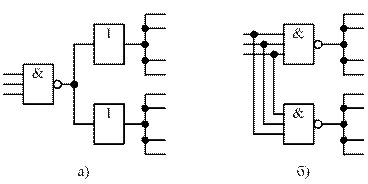
Рисунок 23 – Схема снижения нагрузки на выходах логических элементов с помощью буферных элементов (а) и путем разделения нагрузки (б)

Схемотехника входных цепей элементов КМОП и режимы временно разомкнутых входов

В цифровых устройствах на логических элементах схемотехники КМОП возможна ситуация, когда входы, которые в данное время не используются, не могут быть постоянно подключены к напряжению питания или общей точке схемы, поскольку это исключило бы возможность их последующего перевода в активный режим, т.е. подачу на них информационных сигналов. Оставлять разомкнутыми высокоомные входы также нельзя, так как на них могут наводиться произвольные потенциалы, что чревато опасными последствиями. Поэтому принято фиксировать потенциалы временно разомкнутых входов слабыми сигналами, определяющими потенциалы входов в отсутствие информационных сигналов и не играющими заметной роли при их присутствии.

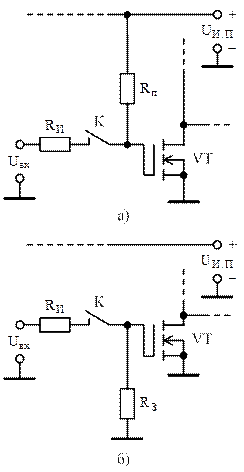
Для исключения паразитных потенциалов к точкам, в которых они могут возникать, подключают специальные резисторы, соединенные с источником питания или с общей точкой схемы. В первом случае это «подтягивающие» резисторы, а во втором – «заземляющие». Цепи с такими резисторами показаны на рисунке 24.

Примечание – « 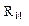» – выходное сопротивление источника сигнала

Рисунок 24 – Схема входной цепи элемента схемотехники КМОП с подтягивающим (а) и заземляющим (б) резисторами

Если подтягивающие и заземляющие резисторы имеют большое сопротивление, то сигналы, формируемые с их участием, относятся к слабым. Когда к «подтянутым» или «заземленным» точкам подключаются сильные информационные сигналы (ключ K на рисунке 24 замкнут), они преодолевают слабые сигналы, так что они практически не влияют на функционирование схем.

В БИС/СБИС программируемой логике нередко к одним и тем же выводам подключают одновременно и подтягивающие, и заземляющие резисторы, последовательно с которыми включены ключевые транзисторы. При программировании выбирается вариант фиксации потенциала вывода и согласно этому выбору замыкается один из ключевых транзисторов [4].

АНАЛИЗ И СИНТЕЗ КОМБИНАЦИОННЫХ

ЦИФРОВЫХ УСТРОЙСТВ

Этапы синтеза комбинационных цифровых устройств

Синтез КЦУ заключается в определении таких способов соединения простейших логических элементов, при которых построенное устройство реализует поставленную задачу по преобразованию двоичной информации.

Синтез КЦУ делится на пять этапов:

1) описание проектируемого узла в содержательных терминах (словесное описание);

2) формализация описания, т.е. составление таблицы истинности синтезируемого узла согласно его назначению и словесному описанию принципа работы;

3) переход от табличного описания синтезируемого узла к логико-математическому описанию в виде логической функции в основном базисе независимо от базиса, который будет использован для построения КЦУ;

4) анализ полученной функции с целью ее упрощения (минимизация);

5) составление функциональной (логической) схемы узла в заданном базисе (для неосновных базисов потребуется предварительное преобразование полученной на четвертом этапе минимальной формы функции из основного базиса в заданный неосновной базис).

В данном случае анализ и синтез выступают как две взаимосвязанные части единого процесса – проектирования цифровых устройств. Анализ может быть самостоятельным процессом, если логическая схема устройства уже имеется и необходимо проанализировать ее работу с целью ремонта либо модернизации.

Канонические формы представления логических функций

Существуют различные формы представления логических функций, но наиболее широкое практическое применение получили канонические (стандартные) формы. К ним относятся:

– совершенная дизъюнктивная нормальная форма (СДНФ);

– совершенная конъюнктивная нормальная форма (СКНФ).

Следует отметить, что любая логическая функция может быть представлена только одной СДНФ (кроме константы нуля) либо только одной СКНФ (кроме константы единицы).

СДНФ логической функции представляет собой дизъюнкцию элементарных конъюнкций, например:

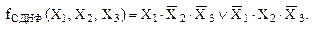(34)

Нормальной эта форма функции называется потому, что состоит из элементарных конъюнкций.

Элементарными называются конъюнкции, сомножителями в которых являются одиночные аргументы либо отрицания одиночных аргументов. Например, конъюнкция 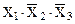является элементарной, а 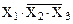– нет. В последнем случае логическая функция не может относиться к СДНФ.

Совершенной эта форма функции называется потому, что элементарные конъюнкции имеют высший ранг, т.е. являются конституентами единицы.

Количество сомножителей в элементарной конъюнкции называется ее рангом. Элементарная конъюнкция высшего ранга называется конституентой единицы. Для n аргументов можно составить 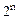конституент единицы, причем для заданных значений истинности аргументов только одна конституента будет равна единице, а остальные – нулю. Например, конституента 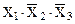принимает значение единица для набора аргументов 100 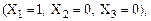а остальные семь конституент для этого набора аргументов будут равны нулю.

Дизъюнктивной эта форма логической функции называется потому, что отдельные конституенты единицы объединяются в одну функцию знаком дизъюнкции.

Правило. Чтобы получить в СДНФ аналитическое выражение логической функции, заданной таблично, необходимо составить дизъюнкцию конституент единицы для тех наборов аргументов, для которых значение функции равно единице, причем символ любого аргумента в конституенте единицы берется со знаком отрицания, если конкретное значение аргумента в рассматриваемом наборе равно нулю.

Например, запишем в СДНФ аналитическое выражение логической функции, заданной в таблице 7, для этого рассмотрим второй, третий, пятый и седьмой наборы аргументов:

Таблица 7 – Таблица истинности для логической функции трех аргументов

Номер набора

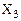
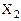
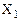
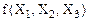
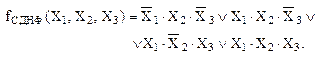(35)

Приведем форму представления логической функции, не являющуюся СДНФ. Например, функция

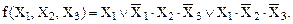(36)

представлена не в СДНФ, а в ДНФ, так как первый член функции имеет первый ранг (для СДНФ каждый член функции должен быть высшего ранга, в данном случае – третьего).

Для перехода от ДНФ к СДНФ необходимо в каждый из членов, в которых представлены не все аргументы, ввести выражение вида 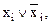где 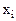– отсутствующий в члене аргумент. Так как 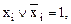такая операция не может изменить значения функции [3].

СКНФ логической функции представляет собой конъюнкцию элементарных дизъюнкций, например:

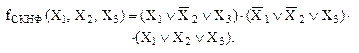(37)

Нормальной эта форма логической функции называется потому, что состоит из элементарных дизъюнкций.

Элементарными называются дизъюнкции, слагаемыми в которых являются оценочные аргументы либо отрицания одиночных аргументов. Например, дизъюнкция 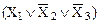является элементарной, а 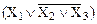– нет. Во втором случае логическая функция не может относится к СКНФ.

Совершенной эта форма функции называется потому, что элементарные дизъюнкции имеют высший ранг, т.е. являются конституентами нуля. Количество слагаемых в элементарной дизъюнкции называется ее рангом. Элементарная дизъюнкция высшего ранга называется конституентой нуля. Для n аргументов можно составить 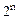конституент нуля, причем для заданных значений истинности аргументов только одна конституента будет равна нулю, а остальные – единице. Например, конституента 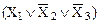принимает значение нуль для набора аргументов 011 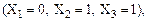а остальные семь конституент для этого набора аргументов будут равны единице.

Конъюнктивной эта форма логической функции называется потому, что отдельные конституенты нуля объединятся в одну функцию знаком конъюнкции.

Правило. Чтобы получить в СКНФ аналитическое выражение логической функции, заданной таблично, необходимо составить конъюнкцию конституент нуля для тех наборов аргументов, для которых значение функции равно нулю, причем символ любого аргумента в конституенте нуля берется со знаком отрицания, если конкретное значение аргумента в рассматриваемом наборе равно единице.

Например, запишем в СКНФ аналитическое выражение логической функции, заданной в таблице 7, для этого рассмотрим нулевой, первый, четвертый и шестой наборы аргументов:

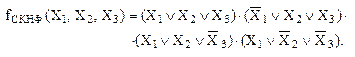(38)

Приведем форму представления логической функции, не являющуюся СКНФ. Например, функция

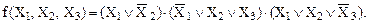(39)

представлена не в СКНФ, а в КНФ, так как первый член функции имеет второй ранг.

Для перехода от КНФ к СКНФ необходимо в каждый из членов, в которых представлены не все аргументы, ввести выражение вида 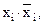где 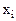– аргумент, не представленный в члене. Так как 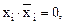то такая операция не может повлиять на значения функции [3].

Исходные положения к минимизации

Как известно, основные параметры логической схемы, например: количество необходимого оборудования (а значит, стоимость) и быстродействие, можно определить по виду логической функции до построения схемы. Это приводит к необходимости оптимизации функции, т.е. к необходимости получения ее оптимального вида по выбранному критерию. В общем случае речь должна идти об оптимизации функции по таким критериям, как быстродействие, надежность (достижение их максимума), количество необходимого оборудования, габариты, энергопотребление, стоимость (достижение их минимума) и т.д. Указанные критерии противоречивы. Например, увеличение быстродействия, как правило, достигается за счет организации параллельной работы данного устройства, но это ведет к увеличению оборудования, а значит, к уменьшению надежности и увеличению стоимости. Поэтому на практике обычно решается частная задача оптимизации по одному из критериев. Чаще всего это делается по минимуму необходимого оборудования, так как при этом, как правило, автоматически решаются задачи получения минимальных габаритов, массы, энергопотребления, стоимости. Такая частная задача оптимизации логической функции носит название минимизации, а форма функции, полученная в результате ее решения, называется минимальной (МДНФ или МКНФ).

Существуют различные методы минимизации, но наиболее широко используются три. К ним относятся:

– расчетный;

– расчетно-табличный (метод Квайна-Мак-Класки);

– табличный (метод Вейча-Карно).

Исходной формой логической функции для любого из этих методов является СДНФ или СКНФ.

Этапы минимизации

При любом методе минимизация выполняется в три этапа.

Первый этап. Осуществляется переход от совершенной формы логической функции (СДНФ или СКНФ) к сокращенной путем выполнения всех возможных склеиваний друг с другом сначала соседних конституент, а затем производных членов более низкого ранга. Таким образом, под сокращенной будем понимать нормальную дизъюнктивную (или конъюнктивную) нормальную форму, членами которой служат только изолированные (несклеивающиеся) элементарные конъюнкции (или дизъюнкции), называемые простыми импликантами (или имплицентами). Например:

(40)

Возможен случай, когда в совершенной форме логической функции нет соседних конституент, тогда сокращенная форма логической функции будет тождественно равна совершенной.

Второй этап. Выполняется переход от сокращенной нормальной формы логической функции к тупиковой. Тупиковой будем называть такую нормальную дизъюнктивную (или конъюнктивную) форму функции, членами которой являются простые импликанты (или имплиценты), среди которых нет ни одной лишней. Термин «лишняя» импликанта или имплицента, означает, что ее удаление не влияет на значение истинности функции. Возможны случаи, когда в сокращенной форме логической фукнции не оказывается лишних членов. Тогда тупиковая форма функции будет тождественно равна сокращенной. Название «тупиковая форма» показывает, что дальнейшая минимизация в рамках нормальных форм уже невозможна.

Третий этап. Осуществляется переход от тупиковой формы функции (минимальной среди нормальных форм) к ее минимальной форме. Этот этап, называемый факторизацией, не является регулярным, как два предыдущих, и требует определенной интуиции и опыта разработчика. Здесь подразумевается поиск возможностей упрощения функции методом проб и ошибок. Для уменьшения числа операций отрицания следует применять закон инверсии, а для уменьшения числа конъюнкций и дизъюнкций – распределительные законы. На этом же этапе решается и вторая задача – приведение логических функций к виду, удобному для применения стандартных логических элементов заданного базиса, которые имеют определенные ограничения по количеству входов и по величине допустимой нагрузки.

Различные методы минимизации отличаются друг от друга путями и средствами практической реализации того или иного этапа. Для минимизации сложных логических функций используются ЭВМ.

Табличный метод минимизации

При табличном методе два первых этапа минимизации (склеивание и поиск лишних членов логической функции) производятся с помощью специальной таблицы, называемой картой Вейча либо картой Карно. Отличие карт Карно от Вейча заключается в способе обозначения строк и столбцов. Карты Карно более удобны в использовании и получили более широкое практическое применение, поэтому в дальнейшем рассмотрим табличный метод минимизации с помощью карт Карно. Третий этап выполняется с помощью алгебраических преобразований. В принципе карта Карно является разновидностью табличной записи некоторой функции, заданной в СДНФ или СКНФ. Она имеет в общем случае вид прямоугольника, разбитого на 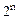малых квадратов, следовательно, число квадратов в карте Карно совпадает с числом строк в таблице истинности. Карты Карно для логических функций трех и четырех аргументов представлены на рисунке 25.

Каждому малому квадрату ставится в соответствие одна из конституент в разложении любой n-аргументной функции. Чтобы задать некоторую функцию с помощью карты Карно, в каждую ее клетку следует записать значение конкретной реализации функции, которое она принимает на соответствующем наборе аргументов. Для нумерации строк и столбцов на карте Карно значения аргументов следует проставлять не в обычном двоичном коде, а в коде Грея (рисунок 25). Особенностью кода Грея является то, что две соседние кодовые комбинации отличаются значениями только одного разряда, следовательно, в смежных по строке либо колонке клетках карты Карно будут находиться соседние конституенты[1] и их можно будет склеивать. Числа в коде Грея можно получить из двоичных чисел путем сложения по модулю 2 с теми же числами, сдвинутыми на один разряд вправо. Например, представление двоичного числа 10 в коде Грея получается следующим образом:

Обозначения столбца и колонки, на пересечении которых находится клетка карты Карно, образуют набор аргументов, значение функции на этом наборе записывается в клетку.

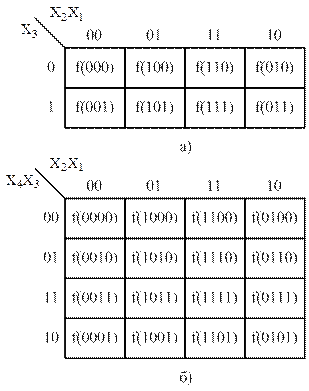
Рисунок 25 – Карты Карно для логических функций трех (а) и четырех (б) аргументов

Рассмотрим пример задания логической функции трех аргументов с помощью карты Карно (рисунок 26), функционирование которой задано с помощью таблицы истинности (таблица 8).

Таблица 8 – Таблица истинности для логической функции трех аргументов

Номер набора

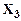
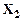
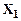
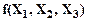
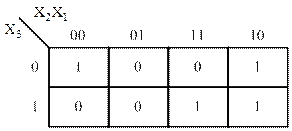
Рисунок 26 – Карта Карно для логической функции трех аргументов, функционирование которой задано таблицей 8

Процесс табличной минимизации с помощью карт Карно осуществляется по следующему правилу:

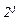смежных заполненных клеток карты Карно, расположенных в виде прямоугольника либо квадрата, соответствуют одной элементарной конъюнкции (дизъюнкции), ранг которой меньше ранга исходных конституент на j единиц. Чем больше клеток в выделенной группе, тем проще выражаемый ею член логической функции.

В любой карте Карно соседние конституенты, к которым можно применить правило склеивания, расположены не только в смежных по строке либо колонке клетках, но и на противоположных концах любой строки и любой колонки.

Таким образом, процесс табличной минимизации сводится к нахождению наиболее крупных замкнутых групп из 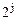заполненных единицами (нулями) клеток. В СДНФ в замкнутые группы объединяют клетки, заполненные только единицами, а в СКНФ – только нулями. Причем надо стараться, чтобы каждая заполненная клетка вошла в какую-либо замкнутую группу и по возможности только в одну. Импликанта (или имплицента), соответствующая некоторой замкнутой группе заполненных клеток, т.е. результат минимизации, будет содержать символы тех аргументов, значения истинности которых совпадают во всех объединенных клетках.