АРИФМЕТИЧЕСКИЕ ОСНОВЫ ЦИФРОВОЙ ТЕХНИКИ 3 страница
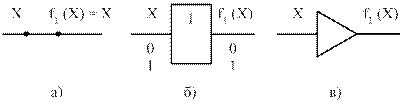
Рисунок 3 – Реализация элементарной логической функции 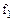 (а) и условное графическое обозначение повторителя (б и в)
(а) и условное графическое обозначение повторителя (б и в)
Повторители в цифровой схемотехнике используются для усиления сигнала по мощности, т.е. для увеличения нагрузочной способности логических элементов.
Логический элемент, реализующий функцию 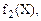 называется инвертором, либо логическим элементом НЕ. Для формирования функции
называется инвертором, либо логическим элементом НЕ. Для формирования функции 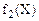 выход логического элемента соединяется со входом через нормально замкнутый контакт электромеханического переключателя, например реле (рисунок 4, а). УГО инвертора по ГОСТ 2.743-91 ЕСКД и международный вариант представлены на рисунке 4, б и 4, в соответственно.
выход логического элемента соединяется со входом через нормально замкнутый контакт электромеханического переключателя, например реле (рисунок 4, а). УГО инвертора по ГОСТ 2.743-91 ЕСКД и международный вариант представлены на рисунке 4, б и 4, в соответственно.
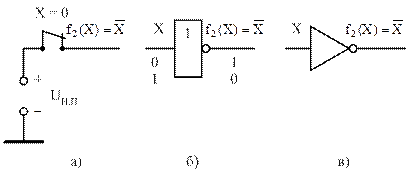
Рисунок 4 – Реализация элементарной логической функции 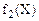 (а) и условное графическое обозначение инвертора (б и в)
(а) и условное графическое обозначение инвертора (б и в)
Таким образом, из всех элементарных логических функций одного аргумента наибольший практический интерес представляет лишь функция 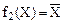 .
.
Элементарные логические функции двух аргументов
Известно, что логические функции могут быть многоаргументными. На основе законов алгебры логики все они могут быть выражены через функции с числом аргументов не более двух. Все логические функции с числом аргументов не более двух являются элементарными, так как содержат только одну логическую операцию.
Рассмотрим все возможные функции двух аргументов. Для этого из таблицы 4 запишем в таблицу 5 их значения истинности, а также рассмотрим их запись, наименование, УГО и название соответствующих логических элементов.
| Таблица 5 – Полная совокупность элементарных логических функций двух аргументов | Условное графическое обозначение | международное | Генератор нуля | 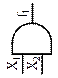
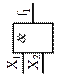
| Конъюнктор (ЛЭ И) | ||
| по ГОСТ 2.743‑91 ЕСКД | 
| 
| |||||
| Наименование функции | Константа нуль (функция 0) | Конъюнкция (логическая операция И) | |||||
| Запись функции | с помощью самостоятельной нотации | 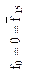
| 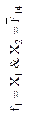
| ||||
| в основном базисе (И, ИЛИ, НЕ) | 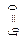
| 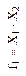
| |||||
| Значения истинности аргументов и функций | |||||||
| Логические аргументы и функции | аргумент 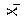
| аргумент 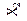
| Функция 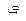
| Функция 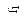
|
| Продолжение таблицы 5 | 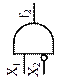
| Элемент запрета (ЛЭ НЕТ) | 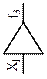
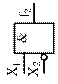
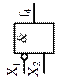
| Повторитель | 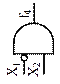
| Элемент запрета (ЛЭ НЕТ) | 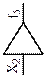
| Повторитель | |
| 
| 
| 
| ||||||
| Запрет первого аргумента (логическая операция НЕТ) | Повторение первого аргумента (логическая операция ДА) | Запрет второго аргумента (логическая операция НЕТ) | Повторение второго аргумента (логическая операция ДА) | ||||||
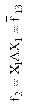
| 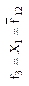
| 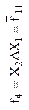
| 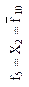
| ||||||
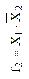
| 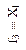
| 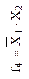
| 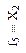
| ||||||
Функция 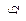
| Функция 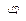
| Функция 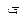
| Функция 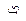
|
| Продолжение таблицы 5 | 
| Сумматор по модулю 2 (ЛЭ Исключающее ИЛИ) | 
| Дизъюнктор (ЛЭ ИЛИ) | 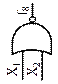
| Элемент Пирса (ЛЭ ИЛИ-НЕ) | 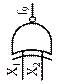
| Эквивалентор (ЛЭ Исключающее ИЛИ-НЕ) | |
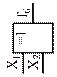
| 
| 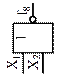
| 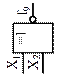
| ||||||
| Неравнозначность, сложение по модулю 2 (логическая операция Исключающее ИЛИ) | Дизъюнкция (логическая операция ИЛИ) | Отрицание дизъюнкции (стрелка Пирса), логическая операция ИЛИ-НЕ | Равнозначность, сложение по модулю 2 с отрицанием (логическая операция Исключающее ИЛИ-НЕ) | ||||||
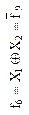
| 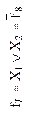
| 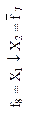
| 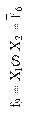
| ||||||
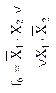
| 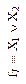
| 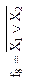
| 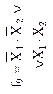
| ||||||
Функция 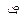
| Функция 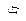
| Функция 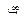
| Функция 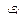
|
| Продолжение таблицы 5 | 
| Инвертор (ЛЭ НЕ) | 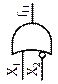
| Импликатор | 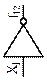
| Инвертор (ЛЭ НЕ) | 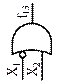
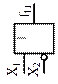
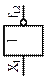
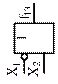
| Импликатор | |

| 
| 
| 
| ||||||
| Отрицание второго аргумента (логическая операция НЕ) | Импликация от 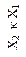 (логическая операция НЕТ-НЕ) (логическая операция НЕТ-НЕ)
| Отрицание первого аргумента (логическая операция НЕ) | Импликация от 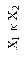 (логическая операция НЕТ-НЕ) (логическая операция НЕТ-НЕ)
| ||||||
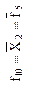
| 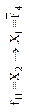
| 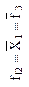
| 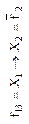
| ||||||
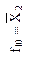
| 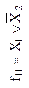
| 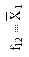
| 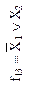
| ||||||
Функция 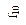
| Функция 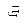
| Функция 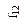
| Функция 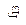
|
| Окончание таблицы 5 | 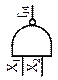
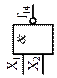
| Элемент Шеффера (ЛЭ И-НЕ) | Генератор единицы | ||
| 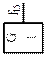
| ||||
| Отрицание конъюнкции (штрих Шеффера, логическая операция И-НЕ) | Константа единица (логическая операция 1) | ||||
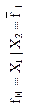
| 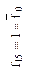
| ||||
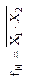
| 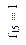
| ||||
Функция 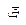
| Функция 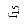
|
Из рассмотренных в таблице 5 функций не представляют практического интереса: 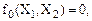
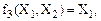
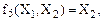
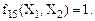
Основные законы и тождества алгебры логики
Логические функции могут быть представлены в различных формах. Эквивалентные преобразования логических функций из одной формы в другую основаны на законах и тождествах алгебры логики. К ним относятся:
– Свойства конъюнкции, дизъюнкции и инверсии:
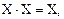
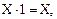
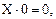
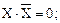 (8)
(8)
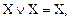
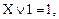
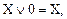
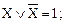 (9)
(9)
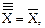
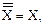 если
если 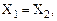 то
то 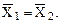 (10)
(10)
Справедливость этих выражений может быть доказана с помощью таблиц истинности.
Второе свойство инверсии 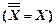 называется законом двойного отрицания.
называется законом двойного отрицания.
– Переместительный (коммутативный) закон справедлив как для дизъюнкции, так и для конъюнкции. Например, для двух аргументов можно записать:
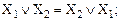 (11)
(11)
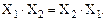 (12)
(12)
Справедливость выражений (11) и (12) можно доказать подстановкой в них различных значений 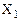 и
и 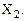 Закон будет справедлив при любом числе аргументов.
Закон будет справедлив при любом числе аргументов.
– Сочетательный (ассоциативный) закон также является симметричным, т.е. справедлив и для дизъюнкции, и для конъюнкции. При логическом сложении (умножении) нескольких аргументов любую группу слагаемых (сомножителей) можно заменить их логической суммой (логическим произведением). Для трех аргументов можно записать:
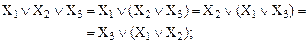 (13)
(13)
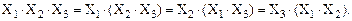 (14)
(14)
– Распределительный (дистрибутивный) закон в алгебре логики (в отличие от обычной алгебры) также является симметричным относительно сложения и умножения, т.е. справедливы его разновидности для логического умножения относительно логического сложения (распределительный закон первого рода) и для логического сложения относительно логического умножения (распределительный закон второго рода). Для трех аргументов распределительный закон первого рода можно записать:
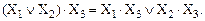 (15)
(15)
Формула (15) справедлива и для большего числа слагаемых в скобках. Для доказательства справедливости выражения (15) следует рассмотреть условия обращения в 0 или в 1 левой и правой частей.
Для трех аргументов в соответствии с распределительным законом второго рода можно записать:
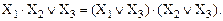 (16)
(16)
Справедливость формулы (16) можно доказать путем непосредственных преобразований. Для этого преобразуем ее правую часть в соответствии с распределительным законом первого рода.
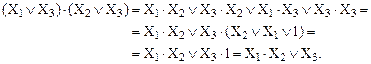
В результате преобразований мы пришли к левой части формулы (16), что и требовалось доказать.
– Закон инверсии (правило де Моргана), как и все предыдущие, симметричен относительно логических сложения и умножения.
Отрицание логической суммы нескольких аргументов равно логическому произведению отрицаний этих же аргументов:
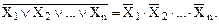 (17)
(17)
Отрицание логического произведения нескольких аргументов равно логической сумме отрицаний этих же аргументов:
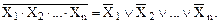 (18)
(18)
Доказательство справедливости выражений (17) и (18) не представляет трудностей, поскольку левые и правые части равны 0 либо 1 при одинаковых условиях.
– Правило старшинства логических операций является следствием закона инверсии и устанавливает очередность выполнения логических операций в логических функциях, т.е. логические операции обладают приоритетом и выполняются в следующей очередности:
– одиночное отрицание;
– конъюнкция;
– дизъюнкция, сложение по модулю 2 и т.д.;
– общее отрицание.
Всякое отклонение от этого порядка должно быть обозначено скобками.
– Правило склеивания обеспечивает упрощение логических выражений и является следствием распределительных законов. Для двух аргументов можно записать:
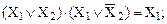 (19)
(19)
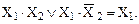 (20)
(20)
Докажем справедливость выражений (19) и (20):
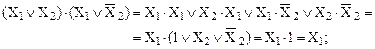
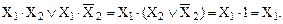
Наименование правила удачно характеризует операцию замены соседних логических сумм (произведений) их общей частью, т.е. два исходных выражения как бы «склеиваются» в одно.
– Правило поглощения также позволяет упрощать логические выражения и является следствием распределительных законов. Для двух аргументов можно записать:
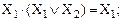 (21)
(21)
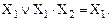 (22)
(22)
Докажем справедливость выражений (21) и (22):
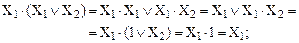
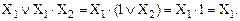
Название рассмотренного правила удачно характеризует операцию замены двух членов логического выражения одним из них.
Понятие базиса и минимального базиса
Элементарные логические функции двух аргументов 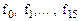 могут быть реализованы простейшими логическими элементами, УГО которых представлены в таблице 5. Для реализации сложных логических функций их сначала следует представить элементарными, которые затем последовательно выполнять с помощью простейших логических элементов. Например, функция
могут быть реализованы простейшими логическими элементами, УГО которых представлены в таблице 5. Для реализации сложных логических функций их сначала следует представить элементарными, которые затем последовательно выполнять с помощью простейших логических элементов. Например, функция 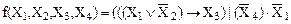 может быть реализована с помощью логической схемы на рисунке 5.
может быть реализована с помощью логической схемы на рисунке 5.
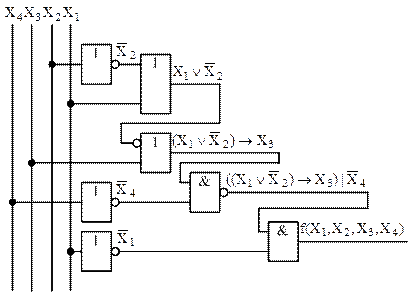
Рисунок 5 – Логическая схема устройства
Имея логические элементы, выполняющие элементарные функции 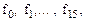 можно реализовать любую сложную логическую функцию. Такая система функций называется полной системой, или базисом. Но это условие не является необходимым, т.е. при синтезе логических устройств можно ограничиться меньшим набором элементарных логических функций, взятых из
можно реализовать любую сложную логическую функцию. Такая система функций называется полной системой, или базисом. Но это условие не является необходимым, т.е. при синтезе логических устройств можно ограничиться меньшим набором элементарных логических функций, взятых из 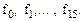
Таким образом, под базисом понимают ограниченный набор элементарных логических функций, с помощью которого можно реализовать логическую функцию любой сложности.
Последовательно исключая из базиса функции, можно получить минимальный базис. Под минимальным базисом понимают такой набор элементарных логических функций, исключение из которого любой функции превращает полную систему в неполную.
Возможны различные базисы и минимальные базисы, отличающиеся друг от друга числом входящих в них функций и видом этих функций. Выбор базиса связан с тем, насколько просто, удобно и экономично можно выполнить логические элементы, реализующие входящие в базис функции, и в целом все логическое устройство.
Один из базисов называется основным. Это базис И, ИЛИ, НЕ, состоящий из трех элементарных логических функций. Основным этот базис называется, потому что при переходе от табличной формы задания к аналитической логическая функция вначале всегда записывается в базисе И, ИЛИ, НЕ, а только затем может быть преобразована в любой другой неосновной базис.
Базис И, ИЛИ, НЕ не является минимальным. Из этой совокупности функций можно исключить функцию И либо функцию ИЛИ. Избыточность основного базиса позволяет упростить схемы логических устройств. Например, если исключить функцию И, то логическую операцию И можно выразить через оставшиеся операции ИЛИ и НЕ. Для этого применим закон двойного отрицания и правило де Моргана:
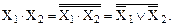 (23)
(23)
Хотя логическую операцию И можно выразить через операции ИЛИ и НЕ, но это сложно (требуется выполнение трех логических операций НЕ и одной операции ИЛИ), поэтому на практике используется неминимальный основной базис.
Рассмотрим некоторые другие базисы. При этом выбранный набор логических функций будет удовлетворять свойствам базиса, если с его помощью можно будет выразить функции И и НЕ (либо функции ИЛИ и НЕ).
Базис образует функция И-НЕ. Действительно, логические операции И и НЕ можно следующим образом выразить через операцию И-НЕ:
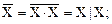 (24)
(24)
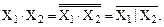 (25)
(25)
Таким образом, из логических функций (24) и (25) следует, что для реализации логического элемента НЕ требуется один логический элемент И-НЕ с объединенными входами, а для реализации логического элемента И – два логических И-НЕ (рисунок 6).
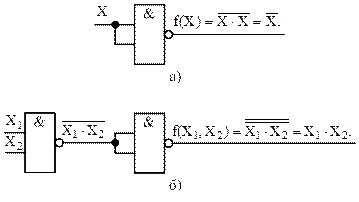
Рисунок 6 – Реализация на основе логических элементов И‑НЕ логических элементов НЕ (а) и И (б)
Следовательно, для построения логического устройства произвольной сложности достаточно иметь логические элементы И-НЕ.
Базис образует функция ИЛИ-НЕ. Докажем, что логические операции НЕ и ИЛИ выражаются через операцию ИЛИ-НЕ:
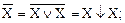 (26)
(26)
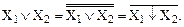 (27)
(27)
Из логических функций (26) и (27) следует, что для реализации логического элемента НЕ требуется один логический элемент ИЛИ-НЕ, а для реализации логического элемента ИЛИ – два логических элемента ИЛИ-НЕ (рисунок 7).
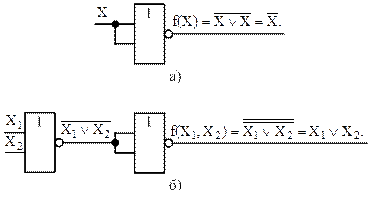
Рисунок 7 – Реализация на основе логических элементов ИЛИ‑НЕ логических элементов НЕ (а) и ИЛИ (б)
Таким образом, используя однотипные логические элементы, реализующие операцию ИЛИ-НЕ, можно построить логическое устройство любой сложности.
В настоящее время базис И, ИЛИ, НЕ обычно используется на начальной стадии проектирования для построения логической схемы устройства. Для реализации устройств чаще всего используются неосновные базисы И-НЕ либо ИЛИ-НЕ. Логические элементы этих базисов широко выпускаются промышленностью в интегральном исполнении.
Преобразование логических функций из основного базиса в неосновные
Рассмотрим примеры преобразования логических функций из основного базиса И, ИЛИ, НЕ в неосновные базисы И-НЕ, ИЛИ-НЕ. Для этого используем закон двойного отрицания и правило де Моргана.
Пример 1. Преобразуем логическую функцию трех аргументов в базис И-НЕ:
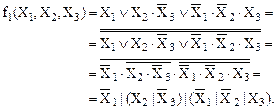 (28)
(28)
Построим логическую схему устройства по конечному выражению функции (28) в базисе И-НЕ (рисунок 8).
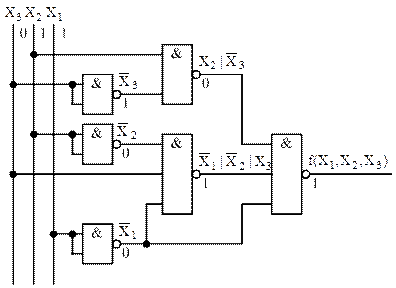
Рисунок 8 – Логическая схема устройства в базисе И-НЕ
Определим значения сигналов на выходе каждого логического элемента и на выходе всей схемы (рисунок 8) для входного кодового слова 011 ( 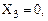
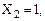
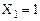 ). Для этого используем таблицу истинности логического элемента И-НЕ.
). Для этого используем таблицу истинности логического элемента И-НЕ.
Дата добавления: 2016-03-22; просмотров: 1559;
