АРИФМЕТИЧЕСКИЕ ОСНОВЫ ЦИФРОВОЙ ТЕХНИКИ 1 страница
Системы счисления. Основные понятия. Выбор системы счисления для цифровых устройств
Система счисления (СС) – это совокупность приемов и правил изображения чисел цифровыми знаками. Системы счисления делятся на позиционные и непозиционные.
В непозиционных СС значение символа не зависит от его положения в числе. Непозиционные СС возникли раньше позиционных. Примером непозиционной СС, дошедшей до наших дней, является римская СС. Например, десятичное число 30 можно представить в виде последовательного ряда из трех одинаковых символов – XXX. Основной недостаток непозиционных СС – большое число различных символов и сложность выполнения арифметических операций.
В позиционных СС значение символа зависит от его позиции в последовательности символов, изображающих число. Например, в десятичном числе 77 первая цифра слева означает количество десятков, вторая – количество единиц. В позиционных СС используется ограниченное количество символов, они более удобны для вычислительных операций, поэтому получили наибольшее распространение.
Основанием позиционной СС называется количество различных символов, используемых для изображения всех чисел в пределах одного разряда.
Любое число X, записанное в позиционной СС, можно представить в виде полинома:
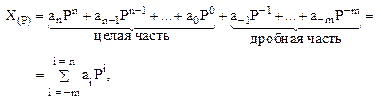 (1)
(1)
где P – основание позиционной СС – целое положительное число; 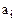 – любая цифра (символ), используемая в данной позиционной СС из множества
– любая цифра (символ), используемая в данной позиционной СС из множества 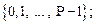
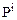 – весовой коэффициент разряда.
– весовой коэффициент разряда.
Например, десятичное число 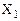 = 123,25 по формуле (1) имеет вид:
= 123,25 по формуле (1) имеет вид:
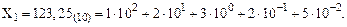
Индекс в круглых скобках указывает на величину основания СС.
Запятая, отделяющая целую часть числа от дробной, находится между разрядами с весовыми коэффициентами 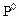 и
и 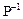 .
.
На величину основания позиционной СС нет ограничения. Поэтому возникает вопрос, какая величина основания P является оптимальной для применения в цифровых устройствах.
Наилучшая система счисления должна обеспечивать простоту технической реализации, простоту выполнения арифметических операций, малые затраты оборудования при построении устройств, высокую помехоустойчивость кодирования цифр и простоту применения математического аппарата для анализа и синтеза цифровых устройств. Краткий анализ систем счисления показывает, что в цифровых устройствах следует применять двоичную СС.
В двоичной СС (P = 2) используются два символа – это цифры 0 и 1. Любое число в двоичной СС записывается в виде последовательности нулей и единиц, расставленных согласно формуле (1). Например, уже рассмотренное нами десятичное число 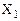 = 123,25 в двоичной СС запишется следующим образом:
= 123,25 в двоичной СС запишется следующим образом:
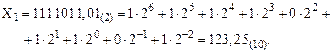
Двоичная СС имеет только один, но крупный недостаток: она не используется человеком (в ней слишком длинными и громоздкими являются числа даже средней величины), а следовательно, ее использование приводит к необходимости преобразования исходных десятичных чисел в двоичную СС, а результатов – из двоичной в десятичную СС. Для таких преобразований чисел требуются достаточно сложные аппаратные средства и дополнительное время. Для преодоления этого недостатка применяется двоично-десятичная СС, представляющая собой СС с основанием P = 10, цифры которой закодированы в виде четырехразрядных двоичных чисел (тетрад). Четырехразрядное двоичное число позволяет получить 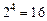 наборов, из которых при двоично-десятичном кодировании используются только 10. Поэтому возможны различные варианты кодирования десятичных цифр в двоичной СС – BCD-коды (Binary Coded Decimal).
наборов, из которых при двоично-десятичном кодировании используются только 10. Поэтому возможны различные варианты кодирования десятичных цифр в двоичной СС – BCD-коды (Binary Coded Decimal).
Наибольшее распространение получил код 8421 (цифры указывают вес соответствующего двоичного разряда двоично-десятичного числа). Например, десятичное число 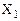 = 123,25 в коде 8421 запишется следующим образом:
= 123,25 в коде 8421 запишется следующим образом:
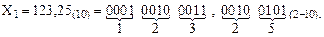
Для преобразования десятичных чисел в код 8421 и обратно используются простые типовые узлы цифровой техники, такие как шифраторы и дешифраторы.
Двоично-десятичные СС используются как для ввода/вывода, так и для обработки числовых данных.
В технике программирования в качестве вспомогательной широкое применение получила шестнадцатеричная СС, у которой основание P = 16, т.е. используется 16 символов – это цифры от 0 до 9 и шесть заглавных букв латинского алфавита: A, B, C, D, E, F. У этой СС основание является целой степенью числа 2, в результате по аналогии с двоично-десятичной СС ее можно определить как систему с основанием P = 16 , у которой символы закодированы в двоичной СС, что значительно облегчает перевод шестнадцатеричных чисел в двоичную СС и обратно. Для этого достаточно перевести в двоичную СС каждый символ исходного числа и записать их в виде тетрад. Например, преобразуем шестнадцатеричное число X = 7B,6 в двоичную СС:
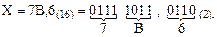
Для обратного преобразования двоичное число разбивают на тетрады влево и вправо от запятой, а затем содержимое каждой тетрады заменяют соответствующим символом шестнадцатеричной СС.
Шестнадцатеричная СС обеспечивает более компактную запись чисел и унификацию форматов числовой и командной информации в виде тетрад.
В заключение рассмотрим таблицу, в которой записаны десятичные числа от 0 до 17, представленные в различных СС (таблица 1).
Таблица 1 – Представление десятичных чисел в позиционных СС
| D (Decimal notation) | B (Binary notation) | H (Hexadecimal notation) | BCD (Binary-Coded Decimal) |
| P = 10 | P = 2 | P = 16 | Код 8421 |
| A | 0001 0000 | ||
| B | 0001 0001 | ||
| C | 0001 0010 | ||
| D | 0001 0011 | ||
| E | 0001 0100 | ||
| F | 0001 0101 | ||
| 0001 0110 | |||
| 0001 0111 |
Перевод чисел из одной позиционной системы счисления в другую
Существует два основных метода перевода чисел из одной СС в другую: табличный и расчетный.
Табличный метод основан на составлении специальных таблиц соответствия чисел в различных СС, примером такой таблицы является таблица 1. Такие таблицы удобны на начальном этапе ознакомления с новой СС, но являются громоздкими.
Расчетный метод более универсален, но применим только к позиционным СС. При использовании расчетного метода могут встретиться три случая: перевод целых чисел, перевод правильных дробей, перевод неправильных дробей.
Правило перевода целых чисел из одной позиционной СС в другую. Исходное целое число необходимо последовательно делить на основание новой СС до тех пор, пока не получится частное, у которого целая часть равна нулю. Деление необходимо производить в исходной СС. Результат перевода записывается из остатков от последовательного деления, причем последний остаток будет старшим разрядом числа в новой СС.
Процесс деления сначала самого числа, а затем целых частей получаемых частных на один и тот же делитель называется последовательным делением.
Пример 1. Переведем десятичное число X = 29 в двоичную и шестнадцатеричную СС:
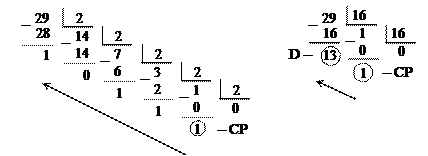
Стрелкой показан порядок записи числа в новой СС.
Ответ: 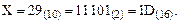
Правило перевода правильных дробей из одной позиционной СС в другую. Исходную правильную дробь необходимо последовательно умножать на основание новой СС до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью перевода. Результат перевода записывается из целых частей произведений, получающихся при последовательном умножении, причем первая целая часть будет старшим разрядом результата. Умножение выполняется в исходной СС.
Процесс умножения сначала самой исходной дроби, а затем дробных частей получаемых произведений на один и тот же множитель называется последовательным умножением.
Пример 2. Переведем в двоичную и шестнадцатеричную СС правильную дробь 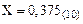 с точностью четыре знака после запятой:
с точностью четыре знака после запятой:
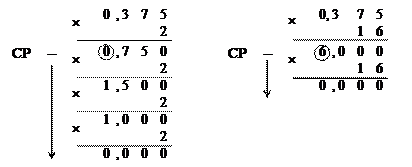 |
Стрелкой показан порядок записи правильной дроби в новой СС.
Ответ: 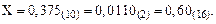
При переводе неправильных дробей отдельно преобразуют целую и дробную части по соответствующим правилам, приведенным выше, а затем записывают результаты перевода через запятую в новой СС.
Пример 3. Переведем неправильную дробь X = 29,375(10) в двоичную и шестнадцатеричную СС с точностью четыре знака после запятой:
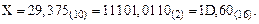
Рассмотренный расчетный метод удобен в том случае, если исходной является десятичная СС. Если же перевод осуществляется из недесятичной СС, то вычисления затруднительны. В этом случае для преобразования чисел можно использовать формулу (1), причем расчеты ведутся в новой СС.
Пример 4. Переведем в десятичную СС двоичное число X = 11101,011:
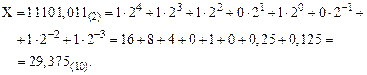
Таким образом, для перевода десятичных чисел в другую позиционную СС используется метод последовательного деления-умножения, а при обратном переводе исходное число записывается в виде полинома и выполняются необходимые расчеты.
Представление двоичных чисел в формах с фиксированной и плавающей точкой
В цифровых устройствах для представления каждого числа используется стандартная разрядная сетка, состоящая из заданного количества двоичных разрядов. Под разрядной сеткой понимают совокупность двоичных разрядов, используемых для представления одного числа. Для знака числа отводится специальный знаковый разряд. Для положительных чисел в знаковом разряде записывается нуль, а для отрицательных – единица.
В зависимости от способа использования разрядной сетки различают две формы представления двоичных чисел: естественную форму (с фиксированной точкой) и нормальную форму (с плавающей точкой).
В естественной форме двоичные числа представляются последовательностью цифр, разделенной точкой на целую и дробную части. Весовые коэффициенты разрядов здесь фиксированы, поэтому и положение точки фиксировано. Наиболее часто цифровые устройства с фиксированной точкой оперируют с двоичными числами, меньшими единицы, у которых точка фиксируется перед старшим разрядом. Для знака числа выделяется дополнительный разряд. Знак числа веса не имеет. Например, двоичное число X = – 0,10110 в разрядной сетке запишется в виде:
В общем случае m – разрядное двоичное число в разрядной сетке цифрового устройства записывается в виде:
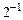
| 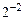
| 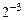
| 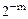
| ||
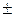
| 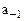
| 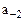
| 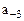
| … | 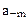
|
 | |
| 
| ||||
| Знак | Разряды модуля числа |
При таком способе фиксации точки минимальное по модулю число, отличное от нуля, представляемое в цифровом устройстве равно:
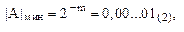
а максимальное – 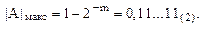
Следовательно, диапазон чисел одного знака, представляемых в таком цифровом устройстве, равен:
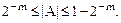
Числа меньше 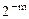 представляются как машинный нуль, а числа больше
представляются как машинный нуль, а числа больше 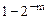 приводят к переполнению разрядной сетки. Область представляемых чисел показана на рисунке 1.
приводят к переполнению разрядной сетки. Область представляемых чисел показана на рисунке 1.

Рисунок 1 – Область представляемых чисел с фиксированной точкой
Достоинством формы с фиксированной точкой является простота выполнения арифметических операций, что обеспечивает простоту арифметического устройства и высокое быстродействие.
Недостатки:
а) узкий диапазон представляемых чисел, что приводит к необходимости использования масштабных коэффициентов;
б) низкая точность представления малых чисел из-за ограниченного числа разрядов в разрядной сетке, что снижает точность вычислений.
В нормальной форме числа представляются с помощью мантиссы и порядка в виде:
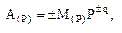 (2)
(2)
где 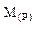 – мантисса числа А;
– мантисса числа А; 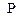 – основание СС; q – порядок числа А.
– основание СС; q – порядок числа А.
Например, десятичное число А = 175 может быть представлено в виде:
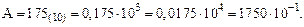
Аналогично в двоичной СС:
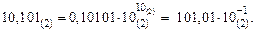
Таким образом, при изображении числа в нормальной форме положение точки не фиксировано. Место точки указывает порядок числа. Она плавает в изображении числа при изменении порядка.
В разрядной сетке цифровых устройств с плавающей точкой помещаются две группы цифр: мантисса со своим знаком и порядок со своим знаком. Основание СС в разрядной сетке не указывается.
Обычно мантиссы чисел выбирают меньше единицы, и при этом всегда в старший разряд заносится единица, т.е. мантисса всегда записывается в нормализованном виде и в таком виде хранится в памяти. Это позволяет более эффективно использовать разрядную сетку. Но при выполнении арифметических операций результаты могут получиться и ненормализированными. Нормализация заключается в сдвиге мантиссы влево на столько разрядов, сколько у нее было нулей после запятой, и в одновременном уменьшении порядка числа на такое же количество единиц.
Пример 4. Нормализуем двоичное число:
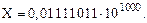
Ответ: 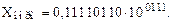
Таким образом, величина нормализованной мантиссы M для двоичных чисел лежит в пределах:
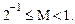 (3)
(3)
Числа с плавающей точкой представляются в разрядной сетке в виде:
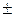
| 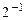
| 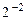
| 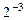
| … | 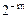
| 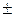
| 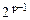
| 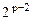
| … | 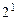
| 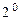
|
| | | 
| | | 
| ||||||||
| Знак мантиссы | Модуль мантиссы (m разрядов) | Знак порядка | Модуль порядка (р разрядов) |
Минимальное по модулю число получается, если взять минимальную мантиссу и максимальный отрицательный порядок:
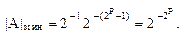
Чтобы получить максимальное по модулю число, необходимо взять максимальную мантиссу и максимальный положительный порядок:
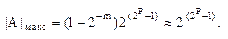
Очевидно, что диапазон представляемых чисел зависит только от числа разрядов порядка. Например, если число разрядов для записи порядка P = 6, то получается 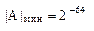 и
и
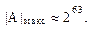
Достоинства:
а) широкий диапазон представляемых чисел, поэтому не нужны масштабные коэффициенты;
б) высокая точность представления как больших, так и малых чисел, так как мантисса нормализована, что обеспечивает высокую точность вычислений.
Недостатком является сложность выполнения арифметических операций, что усложняет схему арифметического устройства и снижает быстродействие.
Таким образом, обе формы представления двоичных чисел имеют свои достоинства и недостатки. Поэтому если требуется высокое быстродействие, то применяют форму с фиксированной точкой, а если требуется высокая точность вычислений, то применяют форму с плавающей точкой.
Способы кодирования двоичных чисел
Кодирование двоичных чисел в цифровых устройствах необходимо для упрощения операции сложения отрицательных чисел, т. е. вычитания. Двоичные числа, представленные в естественной и нормальной формах, кодируются в цифровых устройствах с помощью специальных машинных кодов: прямого, обратного и дополнительного.
Прямой код является простейшим машинным кодом и получается при кодировании в числе только знака. Прямой код положительного числа совпадает с его изображением в естественной форме. Прямой код отрицательного числа совпадает с его изображением в естественной форме, за исключением знакового разряда, в который ставится единица.
Пример 1. 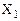 = + 0,11010;
= + 0,11010; 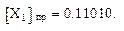
Пример 2. 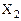 = – 0,11010;
= – 0,11010; 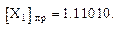
Знак числа веса не имеет и отделяется от цифр числа точкой. Прямой код используется для хранения чисел в памяти, при вводе-выводе информации, а также при выполнении операций умножения и деления. Недостатком прямого кода являются разные правила счета для положительных и отрицательных чисел. Поэтому в цифровых устройствах вычитание (сложение чисел с разными знаками) заменяют операцией сложения чисел в обратном или дополнительном кодах, пропорциональных исходным числам.
Дополнительный код отрицательного двоичного числа находится как дополнения модуля этого числа до граничного числа, представляемого в данной разрядной сетке. Дополнительный код для двоичных чисел, меньших единицы, образуется по формуле:
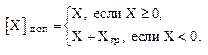 (4)
(4)
где 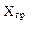 – граничное число,
– граничное число, 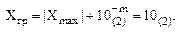
Пример 3. 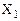 = + 0,1101;
= + 0,1101; 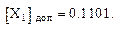
Пример 4. 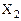 = – 0,1101;
= – 0,1101; 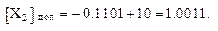
Из формулы (4) и примеров видно, что изображение положительных чисел в дополнительном коде совпадает с изображением их в прямом коде. Для представления отрицательного двоичного числа в дополнительном коде необходимо в знаковом разряде поставить единицу, произвести замену цифр исходного числа на обратные и к полученному коду прибавить единицу младшего разряда.
Обратное преобразование, т.е. получение числа из дополнительного кода выполняется по тому же правилу, что и получение дополнительного кода.
Пример 5. 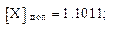
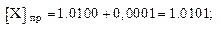
X = – 0,0101.
Дополнительный код получил более широкое применение, так как обеспечивает более высокое быстродействие.
Обратный код отрицательного двоичного числа находится как дополнения модуля до двух без единицы младшего разряда. Обратный код для двоичных чисел, меньших единицы, образуется по формуле:
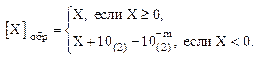 (5)
(5)
Пример 6. 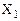 = + 0,1101;
= + 0,1101; 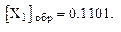
Пример 7. 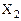 = – 0,1101;
= – 0,1101;
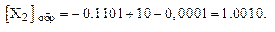
Из формулы и примеров видно, что изображение положительного числа в обратном коде совпадает с его изображением в прямом коде. Обратный код отрицательного числа образуется заменой цифр исходного числа на обратные и постановкой единицы в знаковый разряд.
Переход от обратного кода к прямому осуществляется по тому же правилу, что и от прямого к обратному.
Пример 8. 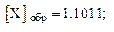
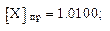 X = – 0,0100.
X = – 0,0100.
Арифметические операции над двоичными числами с фиксированной точкой
Основной операцией, которая используется в цифровых устройствах при различных вычислениях, является операция алгебраического сложения (сложение положительных и отрицательных чисел). Вычитание, умножение и деление также выполняются с помощью операции сложения и некоторых других действий.
Сложение чисел в цифровых устройствах производится так же, как и при ручном счете, т.е. путем поразрядного суммирования чисел, начиная с младших разрядов. Сложение двоичных чисел выполняется в соответствии с таблицей:
| 0 + 0 = 0; | 0 + 1 = 1; | 1 + 0 = 1; | 1 + 1 = 10. |
Пример 1. Выполним сложение двух положительных двоичных чисел, представленных в естественной форме:
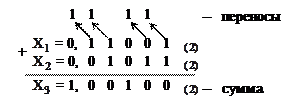
Из примера следует, что начиная со второго разряда сложение производится с учетом переноса из соседнего младшего разряда.
Вычитание двоичных чисел выполняется в соответствии с таблицей:
| 0 – 0 = 0; | 1 – 0 = 1; | 1 – 1 = 0; | 10 – 1 = 1. |
Пример 2. Выполним вычитание, т.е. сложение двух двоичных чисел с разными знаками, представленных в естественной форме:
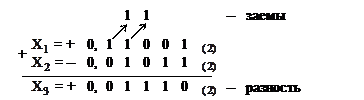
Так как | 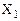 | > |
| > | 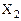 |, то выполняется вычитание
|, то выполняется вычитание 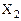 из
из 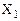 и результату присваивается знак плюс.
и результату присваивается знак плюс.
Из примера следует, что при вычитании происходит заем из соседнего старшего разряда. Следовательно, при сложении и вычитании двоичных чисел в естественной форме используются различные правила, поэтому вычитание заменяется сложением в машинных кодах.
При алгебраическом сложении двоичных чисел в обратном и дополнительном кодах используются следующие правила:
а) знаковые разряды суммируются так же, как и значащие разряды числа;
б) единица переноса из знакового разряда при сложении в дополнительном коде отбрасывается, а в обратном коде для получения правильного результата эта единица прибавляется к младшему разряду суммы, компенсируя величину 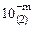 . Такой перенос называется циклическим;
. Такой перенос называется циклическим;
Дата добавления: 2016-03-22; просмотров: 3270;
