Кодирование информации. Постановка задач кодирования
Постановка задач кодирования. Первая теорема Шеннона, кодирование при передаче в канале без помех.
Первая теорема Шеннона декларирует возможность создания системы эффективного кодирования дискретных сообщений, у которой среднее число двоичных символов на один символ сообщения асимптотически стремится к информационной энтропииисточника сообщений (при отсутствии помех).
Вторая теорема Шеннона относится к условиям надежной передачи информации по ненадежным каналам.
Пусть требуется передать последовательность символов, появляющихся с определёнными вероятностями, причём имеется некоторая вероятность того, что передаваемый символ в процессе передачи будет искажён. Теорема Шеннона. утверждает, что можно указать такое, зависящее только от рассматриваемых вероятностей положительное число v, что при сколь угодно малом e>0 существуют способы передачи со скоростью v'(v' < v), сколь угодно близкой к v, дающие возможность восстанавливать исходную последовательность с вероятностью ошибки, меньшей e. В то же время при скорости передачи v', большей v, это уже невозможно. Упомянутые способы передачи используют надлежащие "помехоустойчивые" коды. Критическая скорость v определяется из соотношения Hv = C, где Н — энтропия источника на символ, С — ёмкость (пропускная способность) канала в двоичных единицах в секунду.
Одной из форм представления этой теоремы может служить соотношение Хартли-Шеннона
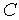 = 2
= 2 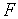 log2
log2 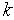 ,
,
где C — пропускная способность (бит/с), 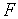 — полоса пропускания линии (Гц),
— полоса пропускания линии (Гц), 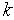
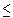 1 +
1 + 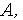
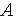 — отношение сигнал/помеха.
— отношение сигнал/помеха.
В теории информатики Теорема Шеннона об источнике шифрования (или теорема бесшумного шифрования) устанавливает предел максимального сжатия данных и числовое значение энтропии Шеннона. Теорема Шеннона об источнике шифрованияпоказывает, что (когда в потоке независимо и одинаково распределенных (НОР) случайных переменных данные стремятся к бесконечности) невозможно сжать данные настолько, что оценка кода (среднее число бит на символ) меньше чем энтропия Шеннона исходных данных, без потери точности информации. Тем не менее можно получить код, близкий к энтропии Шеннона без значительных потерь.
Теорема об источнике шифрования для кодов символов приводит верхнюю и нижнюю границу к минимально возможной длине зашифрованных слов как функция энтропии от входного слова (которое представлено как случайная переменная) и от размера требуемой азбуки.
Исходный код — это отображение (последовательность) из хранилища информации в последовательность алфавитных символов (обычно битов) таких что исходный символ может быть однозначно получен из двоичных разрядов (безпотерьный источник кодирования) или получен с некоторым различием (источник кодирования с потерями). Это идея сжатия данных.
В информатике Теорема об источнике шифрования (Шеннон 1948) утверждает что:
«N случайная переменная с энтропией H(X) может быть сжата в более чем NH(X) битов с незначительным риском потери данных если N стремится к бесконечности, но если сжатие происходит менее в чем NH(X)) бит, то данные скорее всего будут потеряны. (MacKay 2003).»
Теорема об источнике шифрования для кодов символов[править | править исходный текст]
Пусть 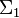 ,
, 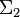 значат два конечных алфавита и пусть
значат два конечных алфавита и пусть 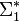 и
и 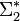 означают набор всех конечных слов из этих алфавитов (упорядоченных).
означают набор всех конечных слов из этих алфавитов (упорядоченных).
Предположим что X — случайная переменная которая принимает значение из 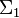 а f — поддающийся расшифровке код из
а f — поддающийся расшифровке код из 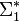 в
в 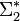 , где
, где 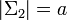 . Пусть S представляет случайную переменную заданную длиной слова f(X).
. Пусть S представляет случайную переменную заданную длиной слова f(X).
Если f является оптимальным в смысле, что она имеет минимальную длину слова для X, тогда
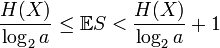
(Shannon 1948)
Доказательство теоремы об источнике шифрования[править | править исходный текст]
Задано 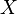 являющееся НОР, его временной ряд X1, …, Xn также НОР с энтропией H(X) iв случае дискретных значений, и с дифференциальной энтропией в случае непрерывных значений. Теорема об источнике шифрования утверждает что для каждого
являющееся НОР, его временной ряд X1, …, Xn также НОР с энтропией H(X) iв случае дискретных значений, и с дифференциальной энтропией в случае непрерывных значений. Теорема об источнике шифрования утверждает что для каждого 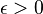 для каждой оценки большей, чем энтропия ресурса, существует достаточно большое n и шифрователь, который принимает n НОР копий ресурса ,
для каждой оценки большей, чем энтропия ресурса, существует достаточно большое n и шифрователь, который принимает n НОР копий ресурса , 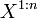 , , и отображает его в
, , и отображает его в 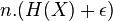 двоичных бит таким способом, что исходный символ
двоичных бит таким способом, что исходный символ 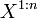 может быть восстановлен из двоичных бит, X вероятностью не менее чем
может быть восстановлен из двоичных бит, X вероятностью не менее чем 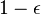 .
.
Доказательство
Возьмем некоторое 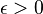 . формула для,
. формула для, 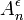 , выглядит следующим образом:
, выглядит следующим образом:
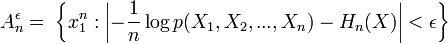
AEP показывает что для достаточно больших n, последовательность сгенерированная из источника недостоверна в типичном случае — 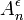 , сходящаяся. В случае для достаточно больших: n,
, сходящаяся. В случае для достаточно больших: n, 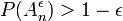 (см AEP)
(см AEP)
Определение типичных наборов подразумевает, что те последовательности, которые лежат в типичном наборе, удовлетворяют:
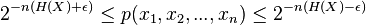
Заметьте, что:
· Вероятность того, что последовательность была получена из 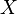
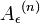 больше чем
больше чем 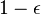
· 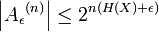 начиная с вероятности полной совокупности
начиная с вероятности полной совокупности 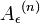 является наиболее большим.
является наиболее большим.
· 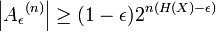 . Fдля доказательства используйте верхнюю границу вероятности для каждого терма в типичном случае, и нижнюю границу для общего случая
. Fдля доказательства используйте верхнюю границу вероятности для каждого терма в типичном случае, и нижнюю границу для общего случая 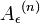 .
.
Начиная с 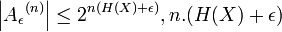 битов достаточно, чтобы отличить любую строку
битов достаточно, чтобы отличить любую строку
Алгоритм шифрования: шифратор проверяет является ли ложной входящая последовательность, если да, то возвращает индекс входящей частоты в последовательности, если нет, то возвращает случайное 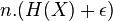 digit number. численное значение. В случае если входящая вероятность неверна в последовательности (с частотой примерно
digit number. численное значение. В случае если входящая вероятность неверна в последовательности (с частотой примерно 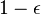 ), то шифратор не выдает ошибку. То есть вероятность ошибки составляет выше чем
), то шифратор не выдает ошибку. То есть вероятность ошибки составляет выше чем 
Доказательство обратимости Доказательство обратимости базируется на том, что требуется показать что для любой последовательности размером меньше чем 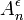 (в смысле экспоненты) будет покрывать частоту последовательности, ограниченную 1.
(в смысле экспоненты) будет покрывать частоту последовательности, ограниченную 1.
Доказательство теоремы об источнике шифрования для кодов символов[править | править исходный текст]
Пусть 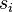 длина слова для каждого возможного
длина слова для каждого возможного 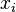 (
( 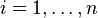 ). Определим
). Определим 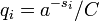 , где С выбирается таким образом, что:
, где С выбирается таким образом, что: 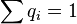 .
.
Тогда
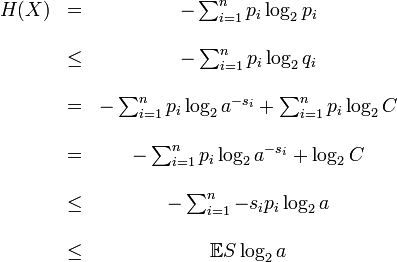
где вторая строка является неравенством Гиббса, а пятая строка является неравенством Крафта 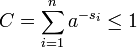
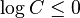 .
.
для второго неравенства мы можем установить
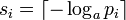
и так
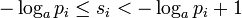
а затем
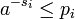
и
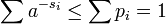
таким образом минимальное S удовлетворяет
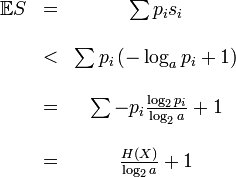
Тема: Результаты Шеннона и проблемы кодирования.
Дата добавления: 2016-03-22; просмотров: 908;
