Пример доказательства выводимости правильного умозаключения
методом резолюции. 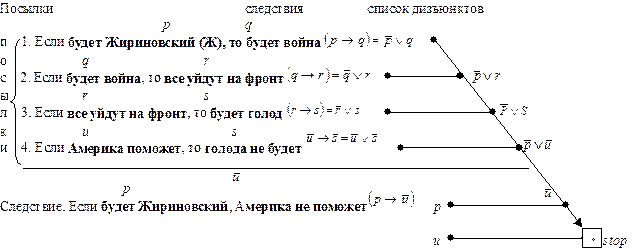 Доказательство «от противного». Пусть следствие (умозаключение) ложно, т.е.
Доказательство «от противного». Пусть следствие (умозаключение) ложно, т.е.  , тогда
, тогда  . Список дизъюнктов –
. Список дизъюнктов – 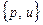 добавляется к списку дизъюнктов посылок.
добавляется к списку дизъюнктов посылок.
- Алгоритм проверки выводимости правильного построенного умозаключения Вонга (Wong, 1960, США)
(1960 г. Гарвард).
Выводимость P из S означает, что из множества посылок
 ⊦
⊦  множество следствий.
множество следствий.
Это соответствует логической формуле  или более детально
или более детально
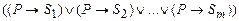 , где
, где  .
.
Правильно построенному рассуждению (умозаключению)  должна соответствовать тавтология
должна соответствовать тавтология  .
.
Каждая 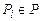 и
и 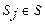 суть ППФ, построенная из связок &, Ú, ù, ®.
суть ППФ, построенная из связок &, Ú, ù, ®.
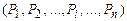 ⊦
⊦ 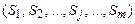 называется строкой Вонга.
называется строкой Вонга.
Правила обработки строки Вонга, приводящие к доказательству выводимости P ⊦ S таковы, что каждое правило суть логический закон и является тождественно истинным преобразованием.
Пусть дана строка Вонга
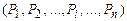 ⊦
⊦ 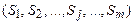
левая часть правая часть
строки строки
1) Замена импликации в строке на ДНФ: 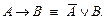
В Рi и Sj, там, где встречается знак «®».
 …⊦
…⊦  … строка с «®»
… строка с «®»
 …⊦
…⊦  … строка ДНФ
… строка ДНФ
2) Избавление от знака отрицания «ù » переносом из одной части строки в другую.
а) 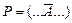 ⊦
⊦  , добавление к правой части.
, добавление к правой части.
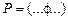 ⊦
⊦ 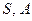 редуцированная строка Вонга.
редуцированная строка Вонга.
б) Р ⊦ 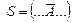 добавление к левой части
добавление к левой части
Р,А ⊦  редуцированная строка Вонга.
редуцированная строка Вонга.
Перенос любой переменной в левую (правую) часть строки всегда вызывает её «отрицание».
 Пример: Избавление от знака отрицания.
Пример: Избавление от знака отрицания.
а) Строка Вонга [( 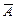 , B) ⊦ (C)] редуцируется в строку
, B) ⊦ (C)] редуцируется в строку
[(B) ⊦ (А, C)]  ⊦ (С) – строка Вонга интерпретируется как логическая формула
⊦ (С) – строка Вонга интерпретируется как логическая формула  . Редуцированная строка Вонга [
. Редуцированная строка Вонга [ 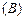 ⊦
⊦ 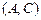 ] и соответствующая формула
] и соответствующая формула  .
.
Правило редуцирования строки Вона является тождественно истинным преобразованием. Доказательство тождественности двух выражений.


Таким образом, если из  выводима С, то из В выводима
выводима С, то из В выводима 
б) 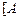 ⊦
⊦  редуцируется в
редуцируется в 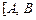 ⊦ С] и соответственно
⊦ С] и соответственно 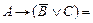


3) Расщепление на строки (левой и правой части строки Вонга).

 а)
а)  ⊦ S ; расщепление левой части
⊦ S ; расщепление левой части
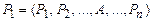 ⊦ S;
⊦ S; 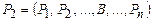 ⊦ S
⊦ S

 б)
б)  ⊦
⊦  ; расщепление правой части
; расщепление правой части
 ⊦
⊦ 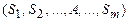 ;
;  ⊦
⊦ 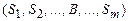
Выводимость (тавтология, тождественная истинность каждой строки должна быть доказана).

 Пример: а)
Пример: а) 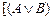 ⊦
⊦ 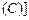 ; расщепление –
; расщепление – 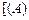 ⊦
⊦ 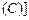 и
и 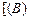 ⊦
⊦ 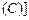 ;
; 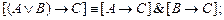

 ;
; 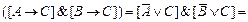
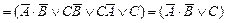
4) Замена логических связок на «,» (правило перечисления).
Строка Вонга
 ⊦
⊦ 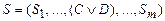
редуцируется в строку
 ⊦
⊦ 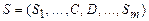
Дата добавления: 2016-03-22; просмотров: 919;
