Скалярное произведение и расстояние для двумерных векторов
Сделав выборку некоторого сигнала f(t), возьмём из неё два значения f1 и f2. Таким же образом получим два значения для некоторого сигнала g(t).
| g2 |
| f2 |
| f1 |
| g1 |
| f(t) |
| g(t) |
| t |
| g |
| f1 |
| f |
| f2 |
| g2 |
| g1 |
| Представим функции двумерными векторами f=(f1, f2) и g=(g1, g2) |
| Если сделать выборку из N точек, получим N-мерный вектор |
Рис.3.3 - Векторное изображение функции
Что нужно для того, чтобы узнать степень взаимоотношения между двумя сигналами f(t) и g(t), выходя из их значений? Если сделать выборку, состоящую всего лишь из двух значений, то, естественно, степень приближения к первоначальному сигналу не высока. Как было изложено ранее, эта проблема разрешится, если увеличить число элементов выборки. Но пока рассмотрим случай выборки из двух точек.
Итак, определим векторы, содержащие по два элемента из выборки каждого сигнала, иначе говоря, двумерные векторы.
Обозначим их как f и g:
f = ( f1;f2) g = (g1;g2).
Если сигналы выразить через векторы таким образом , то исследование отношений между ними есть исследование отношений между векторами. В чём же заключается такое исследование? Во-первых нужно выяснить, насколько удалены векторы f и g т.е. измерить расстояние между векторами (Рис.3.4 ) . Пусть d(f;g)-расстояние между векторами f и g. Чем меньше значение d, тем ближе векторы f и g, а значит и сильнее, взаимосвязь между ними.
Используя компоненты вектора f , получим:
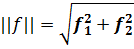 (3.1)
(3.1)
||f|| называют также нормой вектора f.
Итак, из рисунка видно, что расстояние между векторами f и g есть норма вектора f-g. Это можно записать, используя компоненты векторов, в следующем виде:
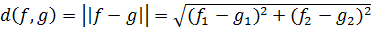 (3.2)
(3.2)
Расстояние – это один из параметров, изменяющих силу связи между векторами. Однако посмотрите на Рис.3.5. На этом рисунке векторы g и h одинаково удалены от вектора f. Но векторы g и f имеют одно и тоже направление, а вектор h расположен под углом к вектору f. Поэтому, увеличив вектор в несколько раз, можно получить вектор g и невозможно получить вектор h. Несмотря на равноудалённость
| f |
| f2 |
| ||g|| |
| g |
| |
| ||f – g|| |
| f1 |
| ||f|| |
| g1 |
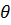
|
| Расстояние между f и g |
Рис.3.4 Расстояние и скалярное произведение двумерных векторов g и h от вектора f, связь f и g гораздо сильнее. Видимо, было бы недостаточно выражать связь между векторами одним лишь расстоянием. Необходимо также учитывать угол между ними. (Рис.3.5).
| h |
| f |
| g |
| d(f, g)=d(f, h), однако сила связи вектора f с векторами g и h неодинакова |
| Проблема в угле |
Рис.3.5. Связь между векторами.
Для выражения связи между векторами используют скалярное произведение между f и g обозначается как (f, g) и определяется как:
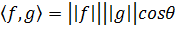
Следовательно,
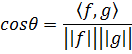
Обозначим эту величину
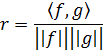
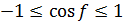 , следовательно
, следовательно
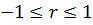 . Величина r выражает силу связи между векторами f и g через угол между ними (Рис.3.6.). Если направление f и g cсовпадают, то r принимает максимальное значение, равное 1. С увеличением угла f значение r уменьшается. Если r=0, т.е. (f, g)=0
. Величина r выражает силу связи между векторами f и g через угол между ними (Рис.3.6.). Если направление f и g cсовпадают, то r принимает максимальное значение, равное 1. С увеличением угла f значение r уменьшается. Если r=0, т.е. (f, g)=0
Коэффициент корреляции – это косинус угла между векторами (r= 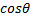 ) )
|
Если векторы перпендикулярны, то их скалярное произведение равно 0. 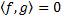
|
r=1
( 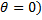
|
| f |
| g |
| g |
r=-1
( 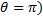
|
| f |
| f |
r=0
(g и f перпендикулярны)
( 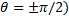
|
| g |
Рисунок 3.6 – Коэффициент корреляции
Векторы f и g взаимно перпендикулярны. Назовём величину r коэффициентом корреляции. Как видно из соотношения (3.4), r зависит от угла между векторами и не зависит от нормы векторов.
Как выразить скалярное произведение, используя компоненты вектора? Это можно сделать следующим образом:
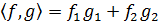
Чтобы вывести эту формулу, применим теорему косинусов для векторов (Рис. 3.4):
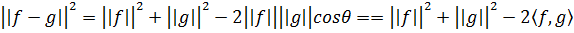
Следовательно,
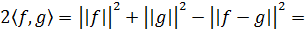
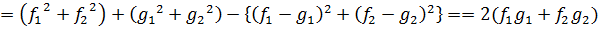
Кстати, скалярное произведение вектора f на самого себя равно:
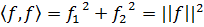 (3.6)
(3.6)
И выражает связь между скалярным произведением и нормой.
Подставим полученные результаты в выражение коэффициента корреляции (3.4) и представим r следующим образом:
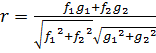 (3.7)
(3.7)
Ортонормированный базис:
Для определения одномерных величин достаточно одного параметра. Например, при измерении длины используют один стандарт величины (сантиметры, миллиметры). Если принять, что 1 см – единица измерения, то 5 см больше 1 см в 5 раз, следовательно, выражается как 5 единиц. Также и в векторном пространстве принято выбирать единицу измерения, которая выражает стандарт величины. Однако в двумерном пространстве одного параметра, измеряющего величину, недостаточно. Необходимо два параметра.
Пара взаимно перпендикулярных векторов {v1;v2} называется ортогональным базисом. Кроме того, если ||v1||=||v2||=1, то эта пара называется ортогональным базисом. Вектор с нормой, равной 1, называется единичным вектором. Иначе говоря, единичный вектор-это вектор, выражающий величину одной единицы измерения. Следовательно, ортонормированный базис представляет собой пару взаимно перпендикулярных единичных векторов, которые в совокупности с парой параметров дают величину вектора.
Выразим вектор f через векторы ортонормированного базиса v1,v2 и совокупность коэффициентов C1,C2(Рис.3.7.):
Выражение вектора через ортонормированный базис
| f |
| n1 |
| n2 |
| C1n1 |
| C2n2 |
| Ортонормированный базис – это пара взаимоперпендикулярных единичных векторов {n1, n2} |
| Для любого вектора – f=C1n1+C2n2 |
| Коэффициенты – это скалярные произведения: C1= <f, n1>, C2=<f, n2> |
f = С1v1+C2v2
Коэффициенты (С1,С2) выражают величину составляющих вектора f в направлении v1 в направлении v2. Иначе говоря, определяют величину вектора. Любой вектор на плоскости можно выразить через это соотношение. Векторы C1v1 и C2v2 называют проекциями вектора f.
3.5 Переход от векторного пространства к пространству функций:
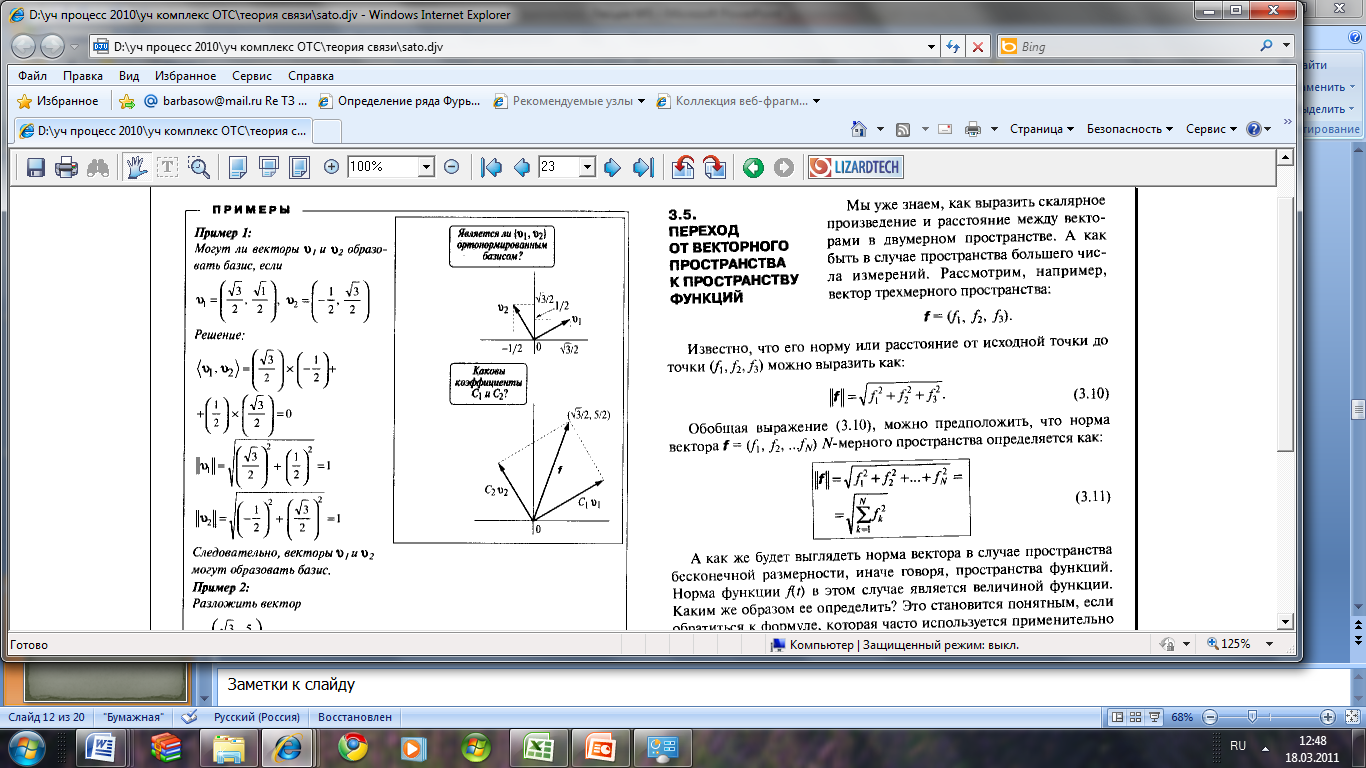
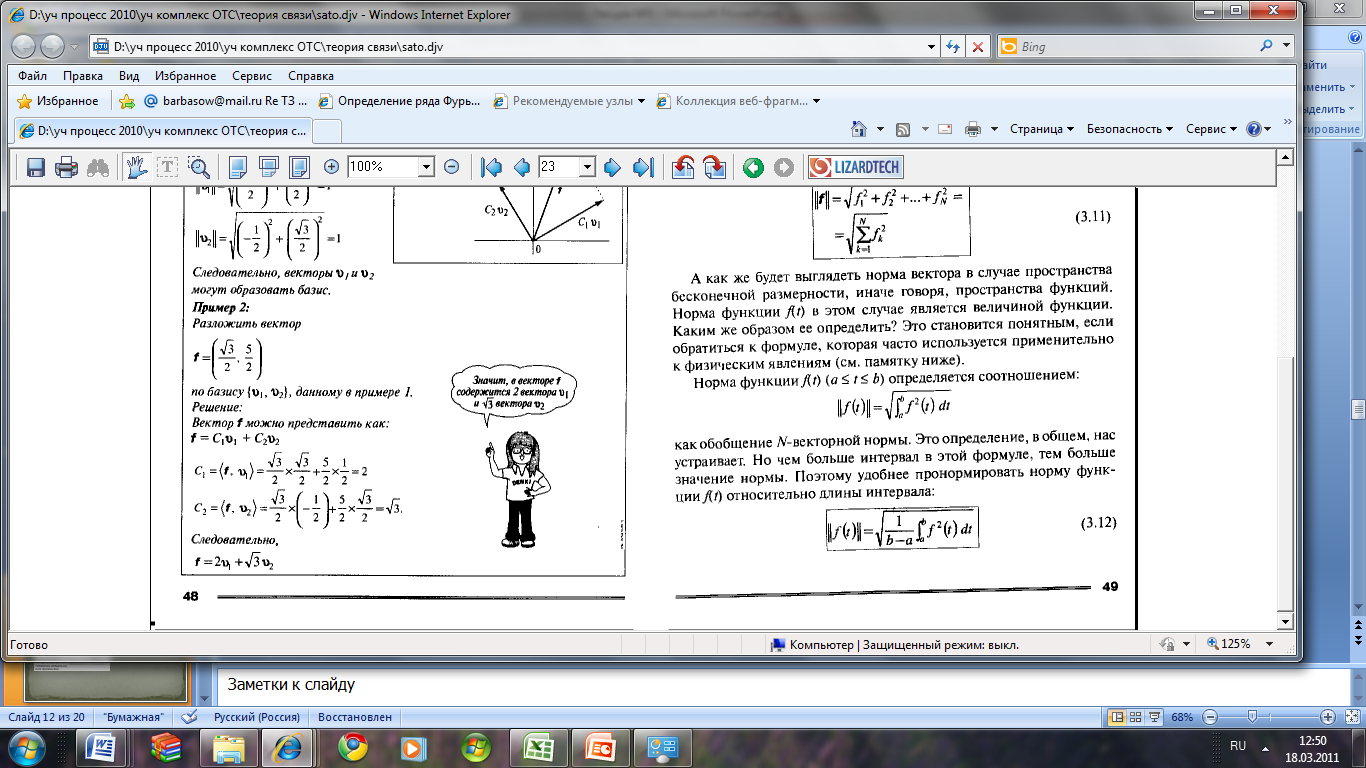
Мы уже знаем, как выразить скалярное произведение и расстояние между векторами в двумерном пространстве. А как быть в случае пространства большего числа измерений. Рассмотрим, например, вектор трехмерного пространства:
f =(f1, f2, f3)
Известно, что его норму или расстояние от исходной точки до точки
(f1,f2,f3) можно выразить как:
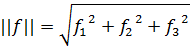 (3.10)
(3.10)
Обобщая выражение (3.10), можно предположить, что норма вектора
f =( f1,f2,……,fN) N- мерного пространства определяется как:
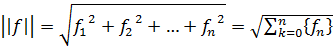 (3.11)
(3.11)
А как же будет выглядеть норма вектора в случае пространства бесконечной размерности, иначе говоря, пространства функций. Норма функции ʃ(t) в этом случае является величиной функции. Каким же образом её определять? Это становится понятным, если обратиться к формуле, которая часто используется применительно к физическим явлениям(см.памятку ниже).
Норма функции f(t) (а≤t≤b) определяется соотношением:
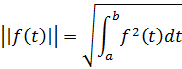
Как обобщение N-векторной нормы. Это определение, в общем, нас устраивает. Но чем больше интервал в этой формуле, тем больше значение нормы. Поэтому удобнее пронормировать норму функции f(t) относительно длины интервала
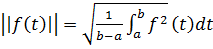 (3.12)
(3.12)
3.6. Система ортонормированных функций:
Мы уже знаем, как выразить вектор f двумерного пространства через ортонормированный базис векторов (V1,V2):
f = С1v1+C2v2
Таким же образом через ортонормированный базис можно выразить и в N-мерном пространстве(На рис.3.9 показан ортонормированный вектор в трехмерном пространстве).
| C3n3 |
| C1n1 |
| C2n2 |
| n3 |
| n2 |
| n1 |
| f |
Рис. 3.9 - Выражение вектора 3-мерного пространства через ортонормированный базис
Ортонормированный базис- это множество взаимно перпендикулярных единичных векторов. Множество векторов (Vk,k=1,2,….N) в N-мерном пространстве, где:
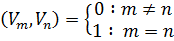
(т.е. Vm и Vn взаимно перпендикулярны и являются единичными), называется ортонормированным базисом N-мерного пространства. Для их выражения используется символ Кронекера δmn:
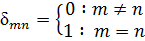
И в упрощённом виде записывается следующим образом:
(Vm, Vn)=δmn
Если все векторы взаимно перпендикулярны, то ни один из них нельзя выразить через другие векторы. Иначе, говоря, они независимы.
Используя ортонормированный базис векторов, можно представить вектор в виде линейной комбинации базисных векторов, можно представить вектор в виде линейной комбинации базисных векторов. Иначе говоря, N-мерный вектор можно представить в виде:
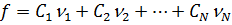
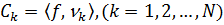
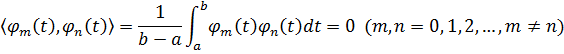
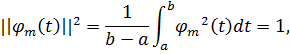
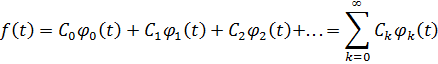
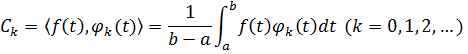
Пример
Образует ли система функций 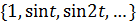 на отрезке
на отрезке 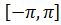 систему ортонормированных функций?
систему ортонормированных функций? 
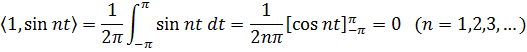
Следовательно, 1 и 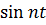 взаимно перпендикулярны.
взаимно перпендикулярны.
Если 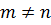 , то
, то
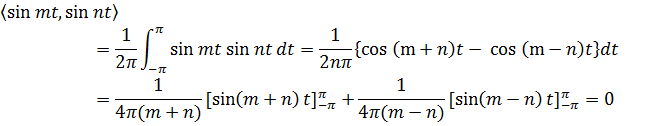
Следовательно, 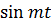 и
и 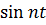
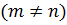 также взаимно перпендикулярны.
также взаимно перпендикулярны.
Шпаргалка
Формулы разложения произведения тригонометрических функций на сумму
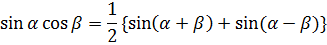
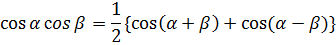
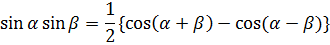
Из вышеизложенных результатов ясно, что множество функций 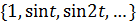 образуют систему ортогональных функций. Однако норма каждой функции:
образуют систему ортогональных функций. Однако норма каждой функции:
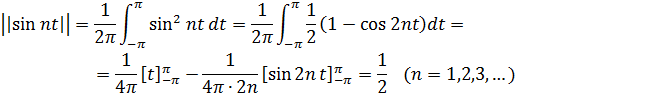
Шпаргалка
Формулы половинного угла
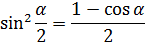
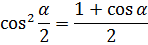
Норма каждой функции не равна 1, следовательно функции не являются ортонормированными
Если норма ||f(t)|| функции f(t) не равна 1, то создадим новую функцию f*(t):
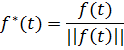
Очевидно, что норма f*(t) равна 1. Подобная операция называется нормировкой системы функций. В нашем случае:
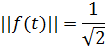
Поэтому, представляя исходную систему функций в новом виде:
(1, 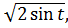
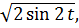 …).
…).
Получим множество функций, образующих систему ортонормированных функций.
Обобщение:
1. Если для непрерывного сигнала f(t) произведена выборка из N значений, то этот сигнал можно представить в виде N-мерного вектора, который соответствует одной точке N-мерного пространства.
2. Величина сигнала выражается нормой вектора, а отличие двух сигналов - расстоянием между векторами. Скалярное произведение векторов - это произведение проекции одного вектора на длину другого. Коэффициент корреляции выражает угол между векторами, а также степень похожести сигналов. Чем больше по абсолютной величине коэффициент корреляции, тем более похожи сигналы. Если он равен 0, то векторы, отображающие сигналы, взаимно перпендикулярны.
Дата добавления: 2016-03-22; просмотров: 2974;
