Виды детерминированных сигналов

Несомненно, представителем детерминированного сигнала является синусоидальная волна, графически описываемая синусоидой. Синусоида является функцией времени t и записывается в виде:

f (t) =A sin (ωt + θ),

где величину сигнала определяют коэффициент А, называемый амплитудой, ω— угловая частота, θ — начальная фаза.

Можно заметить, что через время T, 2T или же 3T форма сигнала повторяется. Сигналы, повторяющие свою форму через опреде­ленный интервал времени, подобно синусоиде, называют периодическими. Если записать выражение периодического сигна­ла относительного целого числа периодов n (n = 0, ±1, ±2,…) в об­щем виде, получим:

f (t +nT) = f (t)

Кстати говоря, функция синуса с периодом Т= 2π в то же время имеет период, равный 4π, 6π и т.д. Самый короткий период называ­ется основным периодом. Кроме синусоиды, к часто встречающимся периодическим сигналам относятся прямоугольный сигнал, пилообразный сигнал, треугольный сигнал (Рис. 1.4).

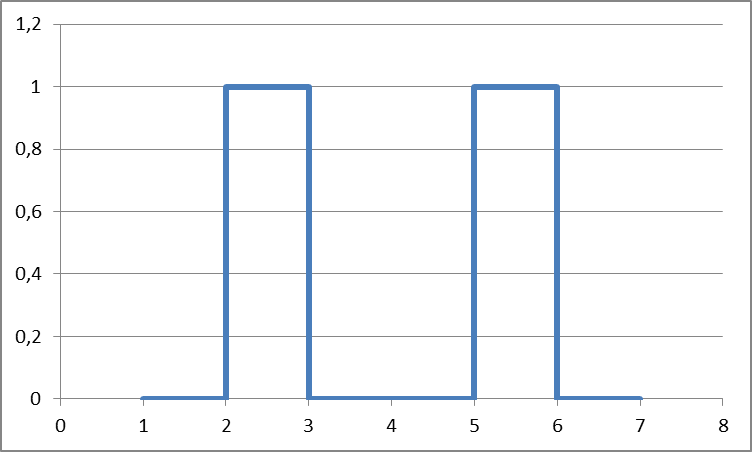
Прямоугольный сигнал

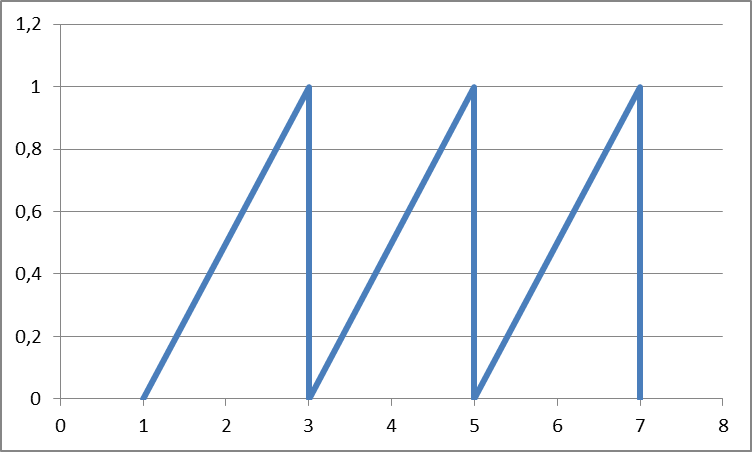
Пилообразный сигнал

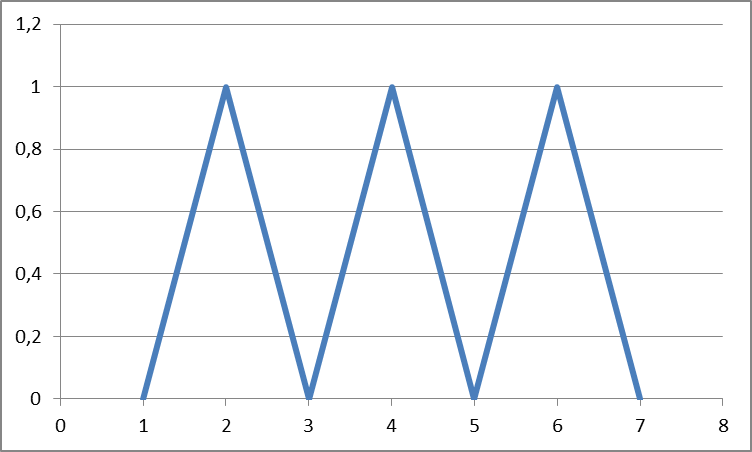
Треугольный сигнал

Рис. 1.4. Основные виды периодических сигналов

Сигнал, концентрирующий энергию в коротком интервале вре­мени, подобно единичному сигналу, изображенному на Рис. 1.5а, называется импульсным сигналом. Сигнал, исчезающий в течение достаточно долгого промежутка времени при ограниченной энергии источника называется затухающим (Рис. 1.5б). Периодический сигнал сохраняет энергию достаточно долго и, поэтому, конечно, не является затухающим.

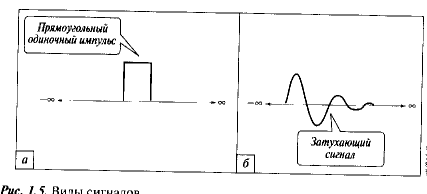
Рис. 1.5. Виды сигналов

В системе прямоугольных координат, изображенных на схеме, рассмотрим точку Р, которая движется по окружности с радиусом А и центром вращения О в направлении против часовой стрелки с постоянной скоростью. Величина, выражающая скорость движения по окружности, называется угловой скоростью ω и определяется числом оборотов за одну секунду.

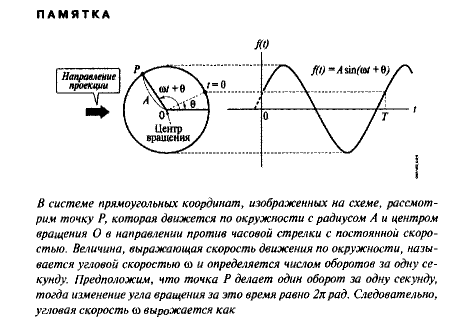
Предположим, что точка Р делает один оборот за одну секунду, тогда изменение угла вращения за это время равно 2π рад. Следовательно, угловая скорость ω выражается как:

ω = 2π рад/с.

Если же за одну секунду тонка Р делает два оборота, ω = 4π рад/с. Вооб­ще, если тонко Р за одну секунду делает число оборотов fс, то угловая частота выражается как:

ω = 2π fс рад/с.

Это число оборотов fc за одну секунду называется частотой вращения и измеряется в герцах. Время, необходимое для одного оборота, называется периодом. Например, при угловой частоте, равной 4π рад/с, время одного оборота точки Р ровно 0.5 секунды. Следовательно, период равен 0.5 се­кунды. При угловой частоте π рад/с величина периода будет равна двум секундам. Период Т, частота вращения fс и угловая частота ω взаимосвя­заны следующим образом:

fс= 1/T, ω = 2π/T.

Положение точки Р, равномерно движущейся по окружности, можно за­писать как функцию f(t), зависящую от времени t:

f (t) =A sin (ωt + θ),

где А — амплитуда, θ— угол поворота при t = 0, называемый начальной фазой.